Hola de nuevo amigos de steemit
Para este post continuo con la explicación de la teoría de combinaciones abordada anteriormente desde las variaciones, para los interesados en el tema los invito a ver combinaciones-permutación. Recordemos que las permutaciones son variaciones de m elementos tomados m a m, para formar grupos según las presentes condiciones:
- Grupos con distintos componentes
- Grupos con iguales componentes, pero dispuestos en orden distintos
Y para tales procesos concluimos escribir las permutaciones en su expresión matemática de la siguiente forma:
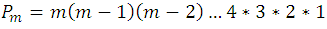
Ahora para definir combinaciones se siguen formando grupos, pero bajo otras concidiones descritas así:
Dados m elementos, llamaremos combinaciones de orden n con m
n a los diferentes grupos que se pueden formar tomando n de los m elementos dados, de manera que dos cualesquiera de esos grupos se consideran diferentes cuando difieran en uno, al menos, de sus elementos.
Como ven a diferencias de las variaciones en este proceso no importa el orden en que estén dispuestos los elementos. Por ejemplo abcd y cadb son variaciones distintas pero una misma combinación; solo un conjunto que contenga algún otro elemento, por ejemplo, abde, se considera como una nueva combinación.
Para comprender mejor como se forman las combinaciones, tomemos, por ejemplo y de nuevo las cuatro letras: a, b, c, d, y escribamos sus combinaciones de primer orden, segundo, tercero y cuarto. Entonces resulta:
Para las de primer orden son:
Para las de segundo orden, se agregan sucesivamente a las del primer orden las letras que le siguen:
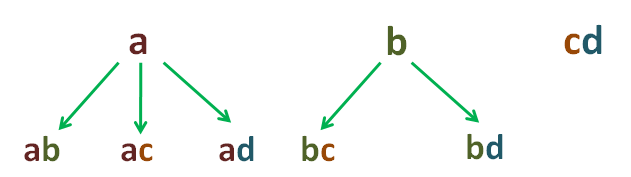
Las combinaciones de tercer orden se obtienen agregando a cada del segundo orden las letras que le siguen en sucesión, una a una: resulta así:
Puede notarse que a las combinaciones ad, bd y cd, no les sigue ninguna letra en sucesión, por lo tanto no hay combinaciones de tercer orden para estas. Las de cuarto orden se obtienen agregando las letras que le siguen en sucesión, una a una, de manera que nos queda :
Es evidente que las combinaciones abd, acd y bcd no les siguen ninguna letra en sucesión y por ello quedan descartada, entonces con estas mismas observaciones se pueden realizar ejemplos similares, luego en general, podemos decir que:
- Dados m elementos, las combinaciones de orden n ( n
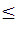m) se forman agregando a las combinaciones de orden ( n-1) los elementos que le siguen en sucesión, uno a uno, mientras existan estos últimos.
Calculo del numero de combinaciones
El número de combinaciones de orden n que pueden formarse con m elementos se designa por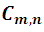 
, ahora para calcular este numero seguimos con nuestro ya típico ejemplo:
En efecto consideremos el conjunto formado por los elementos a, b, c y d. Si formamos todas las variaciones binarias con esos cuatro elementos, y las ordenamos por verticales, en forma tal que en cada vertical figuren las permutaciones de los mismos elementos, se tiene:
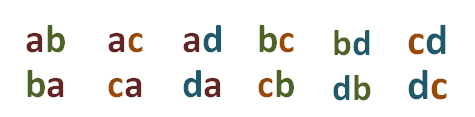
El numero de estas variaciones es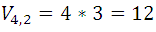 
, pero de ellas las combinaciones de segundo orden de esos mismos elementos ( aparecen en la primera o segunda fila, por ser iguales una a una) son tantas como columnas hay, ya que al pasar de una a otra camba por lo menos un elemento, y como cada columna contiene las permutaciones de 2 elementos cuyo numero 
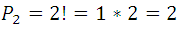, resulta que:
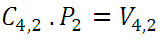
de donde:
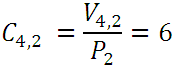
En general, cada combinación de orden n da origen a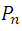 
permutaciones; por ejemplo, la combinación de tres elementos, abc, da origen a 
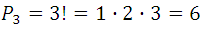permutaciones de tres elementos, las cuales son:
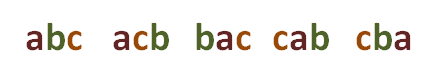
Procediendo en forma análoga con ejemplos similares, en general se puede establecer lo siguiente:
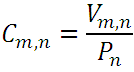
o reemplazando 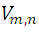a 
y a 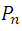por sus valores correspondiente resulta:
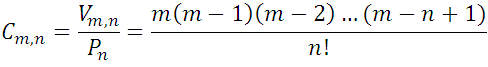
es decir, el número de combinaciones de orden n de m elementos es igual al cociente de dividir el número de variaciones 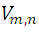por el número de permutaciones .
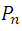Por ejemplo:
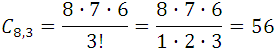
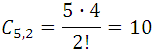
Con el propósito de dar otra expresión a las combinaciones y la cual es muy conocida, multipliquemos los dos términos de la fracción por el numero:
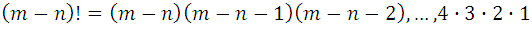
entonces tenemos:
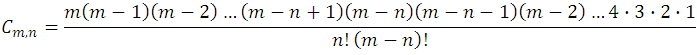
Pero si nos fijamos en el numerador de esta nueva fracción es igual a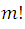 
, por ser una sucesión de factores de números naturales desde 1 hasta m ; luego, sustituyendo este valor en la fracción:
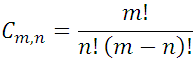
Fórmula, que por aceptar que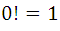 
, es válida para todo valor posible de n, incluso en los extremos n= 0 y m=n.
Por ejemplo la expresión anterior es útil para resolver problemas del tipo:
- Calcular el número de rectas que se forman al unir 7 puntos de un plano, de los cuales nunca hay 3 en línea recta
Análisis: Por geometría se sabe que dos puntos determinan recta y sólo una; el orden de los puntos no importa, pues siempre determinan una misma recta. El problema es entonces de combinaciones de los 7 puntos tomados 2 a 2. Entonces, se tiene:
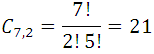
21 rectas se pueden formar al unir 7 puntos de un plano.
- En un plano hay 12 puntos, de los cuales hay 4 en línea recta. Calcular el número de rectas que se pueden trazar al unir los puntos.
Análisis : Si nunca estuvieran en línea recta, el número de rectas que pueden trazarse seria :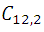 
pero a este numero hay que restarle el número de combinaciones de los 4 puntos de orden 2 que están línea recta y sumar la única recta que resulta de unir estos 4 puntos. Si designamos por N al número de rectas, se tiene:
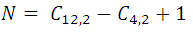
O sea,
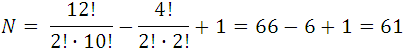
como ven 61 rectas se pueden formar.
Este post es parte de un análisis de las combinaciones de objeto, elementos o todo aquello que se puede expresar a través de números, y explicado aquí lo mas detallado posible. Gracias por tomarse el tiempo para ver este pequeño contenido y espero que sea utilidad o de interés para ustedes.
Bibliografia :