Probabilidades: Aspectos elementales

Hola a todos amigos lectores de steemit

Es de total conocimiento que en hoy día, todo tiende a estar etiquetado desde diferentes perspectivas, el análisis de todo los objetos orgánicos e inorgánicos incluyendo los fenómenos naturales en conjunto, son objetivos de estudios para su posterior divulgación y posición dentro de nuestro sistema intelectual. Una de las herramientas y quizás la mas importante para entender estas investigaciones son los números, las medidas y cálculos aplicados por el método científico especifican los resultados que son utilizados en todas las áreas como la industria, biología, agricultura, tecnología, ciencias sociales y económicas todos estos sectores se manejan por medio del lenguaje numérico.

El afán es tal que incluso se le asigna números a los posibles acontecimientos dentro del marco de eventos deportivos, seguros, pronósticos de clima, tendencia en valores de criptomonedas, contienda electorales, mercado de finanzas son los escenarios de las predicciones que se cuantifican en términos de probabilidades, este es justo el punto a tratar, los aspectos fundamentales que los análisis estadísticos utilizan para calcular dichos valores.

Nociones elementales

La teoría de las probabilidades tuvo su origen en el siglo XVII, cuando algunos matemáticos entre ellos Fermat y Pascal comenzaron a aplicar las leyes de las matemáticas a los efectos del azar, en términos simples la probabilidad es la medida de la posibilidad de que se produzca un suceso, implica la posibilidad de que tal suceso no se produzca. Por ejemplo el caso:

_{Imagen tomada de una fuente de domino público}

¿ Cuál es la probabilidad de escoger el as de espadas en un juego completo de barajas de 40 cartas?
El razonamiento indica que al escoger una carta del juego existen dos posibilidades:

Que sea el as de espadas
Que no sea el as.

Luego el problema cae dentro del cálculo de probabilidades, ya que existe la posibilidad de que el suceso ocurra o no, en efecto cada carta tiene igual probabilidad de aparecer. Las palabras igualmente posibles, aplicadas a sucesos futuros que pueden ocurrir o no por un número de procedimientos, expresa que los mismos están relacionados en forma tal que no existe razón para suponer que alguno de ellos tenga preferencia sobre los demás.

Definición de la probabilidad matemática

Si un suceso puede ocurrir de m maneras, todas igualmente posibles, y si dentro de esas m maneras, n son favorables, la probabilidad favorable p en el primer ensayo es:

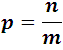
Y la desfavorable q es:

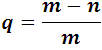
Así por ejemplo la probabilidad de que aparezca un 6 cuando se arroja un dado es:

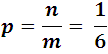
La probabilidad de que no aparezca por lógica es 5/6, otro ejemplo podria ser:

Lanzar 2 dados y ver ¿cuál es la probabilidad de sumar en el primer intento 7 u 8?

_{Gif de uso gratuito tomado de Gifanimados}

Sabemos que cada dado puede caer de 6 maneras, y combinando cada una de ellas con las seis opciones del otro resulta un total de 6x6=36, de manera que lanzar los 2 dados es un suceso que puede ocurrir de 36 formas diferentes y todas igualmente posibles. Para sumar 7, hay que contar los casos favorable que son 1 y 6, 2 y 5, 3 y 4, 4 y 3, 5 y 2, 6 y 1, o sea un total de seis, por consiguiente la probabilidad de sumar 7 es :

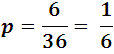
la misma probabilidad de lazar un dado y sacar 1 o 6 en el primer intento, para el caso del 8 sólo puede obtenerse 2 y 6, 3 y 5, 4 y 4, 5 y 3, 6 y 2, es decir, los casos favorables son 8 por lo que la probabilidad es de:

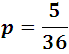
En forma general la suma de las probabilidades favorables y desfavorables es igual a 1. En efecto:

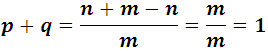
La probabilidad favorable de un suceso es un número comprendido entre 0 y 1. la probabilidad desfavorable a que un suceso ocurra es igual a la unidad menos la probabilidad favorable , es decir, 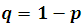, de manera similar, si p es la probabilidad favorable en un ensayo, la probabilidad en k ensayos es kp, así por ejemplo, la probabilidad de que aparezca un 6 cuando se lanza un dado tres veces es 3/6, en 4 veces es 4/6, etc. En 6 ensayos, sería 1, aunque a lo mejor no se consigue, este es un punto muy interesante, que para explicarse adecuadamente es necesario profundizar en la teoría de la probabilidad, en palabras simples significa que los eventos favorables son mucho, pero mucho mas probables que los desfavorable, por lo tanto es casi imposible que un evento contrario se de, o lo que es lo mismo que el evento mas probable es casi seguro que ocurrirá.

Aplicación de la combinatoria al cálculo de probabilidades

Hay casos en los que enumerar todos los eventos igualmente posibles y todos los casos favorables no son tan obvios como los ejemplo anteriores, es mas frecuente ver problemas donde la enumeración resulte fatigosa y conviene entonces disponer de ciertas fórmulas que permitan resolver los problemas con mayor facilidad

Por ejemplo: ¿ Cuál es la probabilidad de sacar 4 tarjetas blancas de una caja que contiene 10 blancas, 4 negras y 3 rojas?

Como pueden observar, el número de maneras en que se pueden elegir 4 tarjetas blancas entre las 10 de ese color es igual al número de combinaciones de 10 objetos tomados de 4 en 4, es decir, es una C_10,4, mientras que el número total de maneras en que se pueden elegir 4 tarjetas entre las 10+4+ 7=17 que contiene la caja C_17,4; por consiguiente, la probabilidad pedida es:

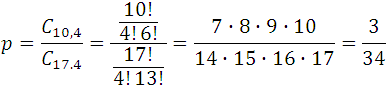
Evidentemente es mucho menor que sacar un 6 al tirar un dado.

Probabilidad compuesta

Cuando dos o mas sucesos ocurren relacionados entre sí, se le denomina acontecimiento compuesto. Son eventos donde las acciones en un primer intento pueden alterar o no otros ensayo, es decir, si queremos sacar de una caja que contiene 5 tarjetas blancas y 8 negras, la cantidad de 6 tarjetas ¿Cuál es la probabilidad de sacar 3 tarjetas blancas y 3 tarjetas negras después?
Es evidente que las probabilidades varían a medida que se van sacando tarjetas, a menos que las tarjetas sean devueltas después del primer intento, partiendo de este caso podemos clasificar los acontecimientos en:

Acontecimientos independientes: son sucesos cuya producción de cada uno de ellos no está influenciada por la producción de los demás.

_{Imagen tomada de Pxhere (CCO)}

Acontecimientos dependientes: sucesos que al producirse afecta a la de otros.

_{Gif tomado de Wikimedia (CCO)}

De esta manera se pueden enunciar 2 propiedades muy importantes:

Si las probabilidades de producción de un grupo de n sucesos son p₁, p₂, p₃,..., p_n la probabilidad de que ocurra todo el grupo de sucesos es

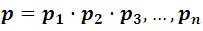
Si arrojamos simultáneamente un dado y una moneda la probabilidad de que aparezca la cara de la moneda y el as del dado, tiene que ser la multiplicación de ambas probabilidad, es decir:

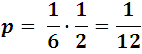
Si p₁ es la probabilidad de que un suceso ocurra y, después de ocurrido, la probabilidad de un segundo suceso es p₂, la probabilidad de que ocurra ambos sucesivamente es p= p₁ . p₂

Sacar sucesivamente 2 ases en una baraja de 40 cartas, tiene una probabilidad de 4/40 en el primer intento, y 3/39 para el segundo intento, por lo que la probabilidad total seria.

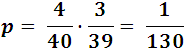
un evento de escasa probabilidad de que ocurra .

Por último tenemos otra eventualidad denominada

Sucesos que se excluyen mutuamente

Ocurre cuando la producción de uno de ellos impide la producción de los demás.

_{Imagen tomada de Pxhere ( CCO)}

La probabilidad total de que se produzca uno u otro de dos sucesos que se excluyen mutuamente o recíprocamente, es igual a la suma de las probabilidades de que ocurra los sucesos por separado.

Por ejemplo supongamos que tenemos una cartera con un billete de 20$ y 3 de 10$, otra cartera con 2 billetes de 20$ y 4 de 10$, y una tercera con 3 billetes de 20$ y uno de 10$. ¿Cuál es la probabilidad de sacar un billete de 20$ de una de las carteras elegida al azar?

Primero es claro que cada cartera tiene la misma probabilidad de ser escogida, luego si elegimos la primera su probabilidad individual seria:

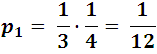
Análogamente para las otras 2 seria:

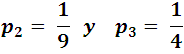
La probabilidad total es entonces:

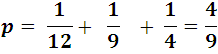
Un valor con casi un 50% de que ocurra.

Estos son los aspectos fundamentales de la teoría de probabilidades, el inicio de métodos estadísticos mas completos que se tornan mas complejos con la evaluación de nuevas variables y otros factores que se asimilan mucho mas a los a procesos de nuestra vida cotidiana, el hecho es que casi nada se escapa de los números ni siquiera la forma de poder predecir el futuro.

Bibliografía referente al texto:

Hasta la próxima steemians

by @juancmz