Conceptos básicos
Quiero aclarar que con estructuras no me refiero a edificios solamente, sino a cualquier conjunto de materiales o elementos destinados a soportar cargas (sean grandes o pequeñas), es decir que prácticamente cualquier cosa es una estructura, desde las plantas y el cuerpo humano, hasta los barcos y los puentes.
Éstas cargas que soportan dichas estructuras, producen esfuerzos que, a su vez, producen deformaciones. Es decir que esfuerzos y deformaciones guardan una relación de causa y efecto. El esfuerzo es la fuerza aplicada por unidad de área, y la deformación es el cambio de tamaño o forma del cuerpo debido a dichos esfuerzos.
Pragmáticos vs teóricos, un poco de historia
A pesar de realizar sus diseños con la ayuda de Dios, y basándose únicamente en la fe y la práctica, los ingenieros no lo venían haciendo tan mal. Hoy en día se mantienen en pie estructuras imponentes como el Acueducto de Segovia (siglo II), la Torre de Pisa (siglo XII), el Acueducto de Pontcysyllte (siglos XVIII y XIX) y la Catedral Metropolitana de la Ciudad de México (del siglo XVI al siglo XIX).
Pero a medida que quiso innovar y mejorar sus diseños, el asunto se fue complicando cada vez más porque, por ejemplo, si quería duplicar el tamaño de una estructura, no siempre era posible aumentar la escala de un diseño ya existente sin obtener resultados desastrosos. Así que se vió en la necesidad de emplear –a regañadientes, diría yo– las matemáticas, para modelar los problemas de la vida real y obtener soluciones –esperaba él– mejores.
Sin embargo, ingenieros pragmáticos como Telford (1757-1834), se rehusaban a utilizar los métodos matemáticos de la época para determinar los esfuerzos que sería capaz de soportar una estructura, pero no porque no quisieran conocer su aproximación numérica, sino porque no confiaban en las formas de llegar a ése resultado. Este escepticismo tenía lugar porque, según los pragmáticos, los teóricos le daban más importancia a sus métodos numéricos que a la validez de sus suposiciones, es decir, seguramente tenían la respuesta correcta, sí, pero a la suma equivocada.
Pero alrededor de 1850 –mejor tarde que nunca-, los ingenieros decidieron que tal vez no era tan mala idea emplear esas matemáticas abstractas que durante tantos años se habían negado a entender –¿O más bien descifrar? -, y comenzaron a hacer cálculos para obras de gran envergadura.
Sin embargo, al realizar los cálculos, notaron que muchas estructuras, de construirse, estarían sometidas a esfuerzos mayores que los que podían soportar los materiales empleados, así que se aseguraron de que los esfuerzos máximos soportados por la estructura (obtenidos del diseño estructural) siempre fuesen menores al esfuerzo máximo que podría soportar el material (obtenido del ensayo de materiales), esto, con un factor de seguridad –¿O de ignorancia? -. Como sea, muchas veces las estructuras se venían abajo y ya no era por obra divina, sino por «materiales defectuosos», o aún más probable, por una reducción del factor de seguridad para economizar.
Lo que los ingenieros no sabían, y que las costureras sí
Aun durante el siglo XIX, algo misterioso ocurría con las embarcaciones. La necesidad de barcos más ligeros, grandes y/o veloces representó un gran desafío, porque aunque se utilizaban materiales con buena reputación, grandes factores de seguridad y todos los cálculos parecían ser correctos, los barcos tenían una extraña tendencia a romperse en dos en medio del océano, incluso en condiciones climáticas normales.
La respuesta a éste problema comenzó a aclararse cuando C. E. Inglis (1875-1952) expuso que, en lo que a distribución de esfuerzos se refiere, los cálculos solamente son válidos, o más bien, confiables, cuando la estructura es lisa y no tiene cambios súbitos de geometría. En otras palabras, habían estado diseñando los barcos con la respuesta correcta a la suma equivocada.
Por lo tanto, las irregularidades geométricas que estaban siendo ignoradas, como hoyos, grietas, muescas y esquinas puntiagudas, no eran tan despreciables como se creía, y fueron la razón por la cual la evolución de las embarcaciones se estancó por tantos años.
Dichas irregularidades geométricas causan que el esfuerzo se incremente de manera importante en una porción, generalmente pequeña, de la estructura. Esto es lo que se conoce como concentración de esfuerzos.
Pero por supuesto, esto ya lo sabían las costureras –aunque de una forma empírica-. Los modistas sabían que, al hacer un pequeño corte en la orilla de un trozo de tela, podía rasgarse fácilmente al tirar de ella.
Pero… ¿Por qué?
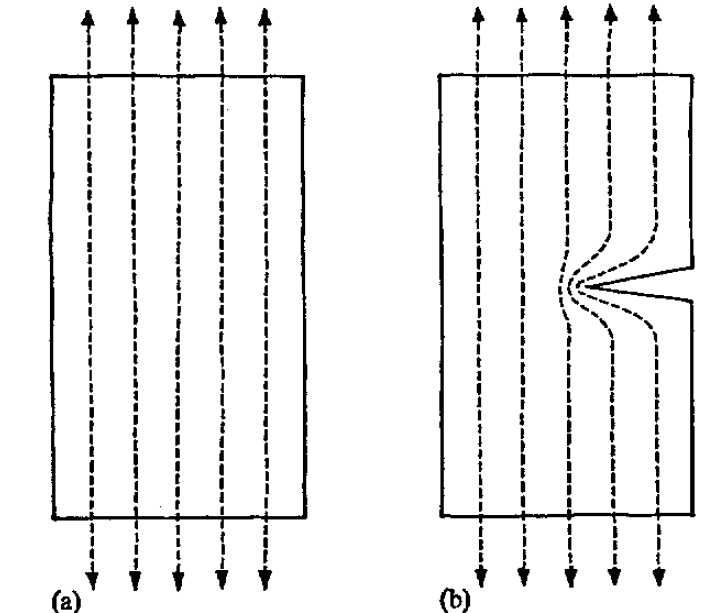
Este fenómeno puede explicarse fácilmente con la siguiente imagen:
En el primer caso, las líneas son rectas y paralelas, lo que quiere decir que la distribución de esfuerzos es uniforme, pero si interrumpimos algunas de éstas haciendo un corte, los esfuerzos se concentrarán alrededor de la grieta como se observa en el segundo caso.
En otras palabras, las líneas no pueden simplemente desaparecer con la rotura o interrupción del material, así que el esfuerzo se incrementa para compensar esta disminución del área. Es por esto que para una misma fuerza F, el esfuerzo en la región cercana al corte será mucho mayor que el esfuerzo actuante en ese mismo lugar antes de hacer el corte.
Esto explica muchas cosas, como el por qué es más fácil cortar una barra de chocolate por las ranuras, o por qué los tickets tienen esas pequeñas perforaciones en los extremos, incluso el porqué de la forma redondeada de las ventanas de barcos, submarinos y aviones.
J. E. Gordon. Structures: or why things don't fall down (1978). Penguin Books.