Saludos a toda la comunidad científica y académica de Steemit, en esta oportunidad continuaremos abordando la temática relativa a las Funciones tocando de forma detallada dos conceptos que generalmente se estudian de forma somera pero no con la profundidad que se amerita para su comprensión y reconocimiento de la importancia que tienen dentro del referido tema, se trata de las nociones de Imagen y Preimagen, las cuales son consideradas subconjuntos de los conjuntos de llegada y partida respectivamente. A lo largo de la presente publicación no sólo abordaremos las definiciones desde las perspectivas teórica y gráfica, asimismo se presentará sus correspondientes propiedades demostrándolas como se ha acostumbrado en trabajos anteriores.
Se invita a los lectores al disfrute académico de las nociones que se compartirán a continuación. Comencemos.

Antes de pasar a definir formalmente el concepto de Imágenes de subconjuntos del dominio es importante destacar que la misma tiene que ver con el contexto de existencia de la función que se está estudiando, esto quiere decir, que se trata de conocer donde un hecho de la vida cotidiana tiene ocurrencia, recordando de publicaciones anteriores que se ha dicho precisamente que las funciones describen o representan hechos de la realidad, dependiendo como las mismas estén definidas. A continuación se procede a plantear la definición matemática del caso:
Sea la función f:A⟶B y X⊂A se define la Imagen del referido subconjunto como el conjunto formado por todas las imágenes de los elementos pertenecientes a X⊂A. Esto es
Es decir
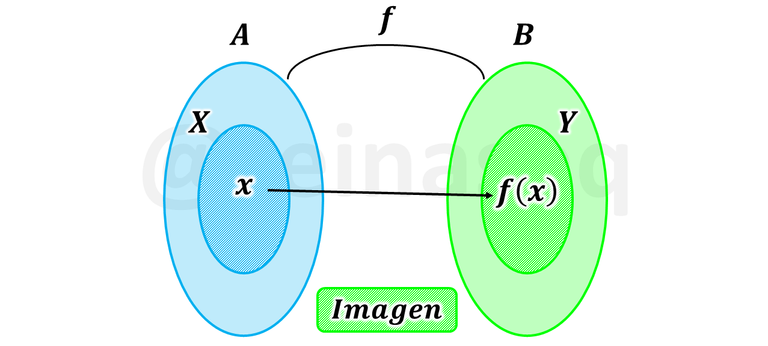
Lo planteado se puede visualizar con claridad en la siguiente representación gráfica
Lo expresado nos indica que se puede plantear una función cuyo Dominio no necesariamente sea todo el conjunto de partida sino una parte de él.

Considerando la función f:A⟶B, X⊂A y Y⊂A se plantean las siguientes propiedades:
- Si se tiene que dados dos subconjuntos del dominio uno de ellos está contenido en el otro, entonces sus respectivas imágenes verifican la misma condición. En símbolos es
Demostrando
En relación a esta propiedad observamos que estamos en presencia de un conectivo condicional lo cual indica que contamos con una hipótesis o argumentos que apoyan la demostración y una tesis que es exactamente lo que se va a comprobar. Adicionalmente, lo que se pide demostrar es una inclusión de conjuntos por lo cual se debe tener presente la respectiva definición. Procedamos:
∀y∈f(X)⟹∃x∈X∧f(x)=y, por definición de imagen
⟹∃x∈Y∧f(x)=y, por hipótesis X⊂Y y por definición de inclusión de conjuntos
⟹y∈f(Y), por definición de imagen
∴ f(X)⊂f(Y), por definición de inclusión de conjuntos∎
- La imagen de la unión de subconjuntos del dominio es igual a la unión de las imágenes. Simbólicamente es
Demostrando
Como se puede apreciar estamos en presencia de una igualdad de conjuntos, lo cual nos indica que se debe demostrar la doble inclusión de acuerdo a lo que estable la definición respectiva. Procedamos a la demostración:
i) f(X∪Y)⊂f(X)∪f(Y)
∀y∈f(X∪Y)⟹∃x∈(X∪Y)∧f(x)=y, por definición de imagen
⟹(∃x∈X∨∃x∈Y)∧f(x)=y, por definición de unión de conjuntos
⟹(∃x∈X∧f(x)=y)∨(∃x∈Y∧f(x)=y), por ley lógica distributiva de la conjunción respecto de la disyunción inclusiva
⟹ y∈f(X)∨y∈f(Y); por definición de imagen
⟹ y∈[f(X)∪f(Y)]; por definición de unión de conjuntos
∴f(X∪Y)⊂f(X)∪f(Y), por definición de inclusión de conjuntos
ii) f(X)∪f(Y)⊂f(X∪Y)
∀y∈[f(X)∪f(Y)]⟹ y∈f(X)∨y∈f(Y), por definición de unión de conjuntos
⟹(∃x∈X∧f(x)=y)∨(∃x∈Y∧f(x)=y), por definición de imagen
⟹(∃x∈X∨∃x∈Y)∧f(x)=y, por ley lógica distributiva de la conjunción respecto de la disyunción inclusiva
⟹∃x∈(X∪Y)∧f(x)=y, por definición de unión de conjuntos
⟹ y∈f(X∪Y); por definición de imagen
∴f(X)∪f(Y)⊂f(X∪Y), por definición de inclusión de conjuntos
∴f(X∪Y)=f(X)∪f(Y), por definición de igualdad de conjuntos∎
- La imagen de la intersección de subconjuntos del dominio es subconjunto de la intersección de las imágenes. Simbólicamente es
Demostrando
En este caso sólo debemos demostrar una inclusión de conjuntos. Procedamos a la comprobación:
∀y∈f(X∩Y)⟹∃x∈(X∩Y)∧f(x)=y, por definición de imagen
⟹(∃x∈X∧∃x∈Y)∧f(x)=y, por definición de intersección de conjuntos
⟹(∃x∈X∧∃x∈Y)∧(f(x)=y∧f(x)=y), por ley lógica de idempotencia de la conjunción
⟹∃x∈X∧(∃x∈Y∧f(x)=y)∧f(x)=y, por ley lógica asociativa de la conjunción
⟹∃x∈X∧(f(x)=y∧∃x∈Y)∧f(x)=y, por ley lógica conmutativa de la conjunción
⟹(∃x∈X∧f(x)=y)∧(∃x∈Y∧f(x)=y), por ley lógica asociativa de la conjunción
⟹ y∈f(X)∧y∈f(Y); por definición de imagen
⟹ y∈[f(X)∩f(Y)]; por definición de unión de conjuntos
∴f(X∩Y)⊂f(X)∩f(Y), por definición de inclusión de conjuntos∎

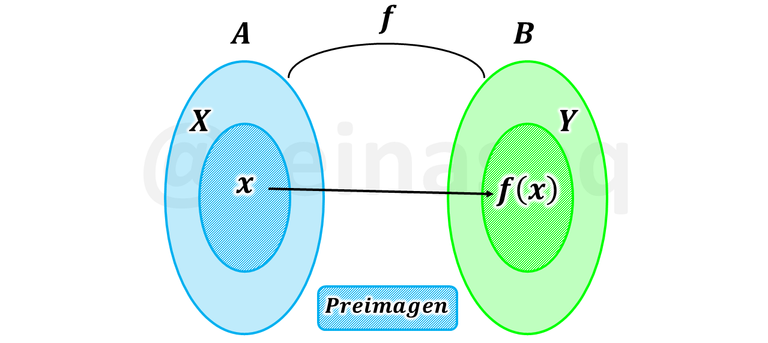
Hablar de preimagen es hacer alusión al elemento a partir del cual se originó la imagen, es decir, a los elementos que pertenecen al dominio de la función que mediante la misma se convierten en algún elemento del codominio o conjunto de llegada. En este sentido, se define formalmente como sigue
Sea la función f:A⟶B, X⊂A y Y⊂B se define la preimagen o la imagen inversa como el conjunto que contiene a todos los elementos del dominio de la función que tienen su imagen respectiva en el conjunto Y⊂B. En símbolos es
Lo cual indica que
Gráficamente tenemos

Considerando la función f:A⟶B, X⊂B y Y⊂B la preimagen verifica las siguientes propiedades:
- La preimagen de la unión es igual a la unión de las preimágenes, lo cual puede expresarse simbólicamente como sigue
Demostrando
Por tratarse de una igualdad de conjuntos, debemos demostrar la doble inclusión. Procedamos:
i) f-1(X∪Y)⊂f-1(X)∪f-1(Y)
∀x∈f-1(X∪Y)⟹f(x)∈(X∪Y), por definición de preimagen
⟹f(x)∈X∨f(x)∈Y, por definición de unión de conjuntos
⟹x∈f-1(X)∨x∈f-1(Y), por definición de preimagen
⟹x∈[f-1(X)∪f-1(Y)], por definición de unión de conjuntos
∴f-1(X∪Y)⊂f-1(X)∪f-1(Y), por definición de inclusión de conjuntos
ii) f-1(X)∪f-1(Y)⊂f-1(X∪Y)
∀x∈[f-1(X)∪f-1(Y)]⟹ x∈f-1(X)∨x∈f-1(Y), por definición de unión de conjuntos
⟹f(x)∈X∨f(x)∈Y, por definición de preimagen
⟹f(x)∈(X∪Y), por definición de unión de conjuntos
⟹x∈f-1(X∪Y); por definición de preimagen
∴f-1(X)∪f-1(Y)⊂f-1(X∪Y), por definición de inclusión de conjuntos
∴f-1(X∪Y)=f-1(X)∪f-1(Y), por definición de igualdad de conjuntos∎
- La preimagen de la intersección es igual a la intersección de las preimágenes, lo cual se expresa simbólicamente como sigue
Demostrando
Procederemos de manera similar a la demostración anterior por tratarse de una igualdad de conjuntos, debemos demostrar la doble inclusión. Comencemos:
i) f-1(X∩Y)⊂f-1(X)∩f-1(Y)
∀x∈f-1(X∩Y)⟹f(x)∈(X∩Y), por definición de preimagen
⟹f(x)∈X∧f(x)∈Y, por definición de unión de conjuntos
⟹x∈f-1(X)∧x∈f-1(Y), por definición de preimagen
⟹x∈[f-1(X)∩f-1(Y)], por definición de unión de conjuntos
∴f-1(X∩Y)⊂f-1(X)∩f-1(Y), por definición de inclusión de conjuntos
ii) f-1(X)∩f-1(Y)⊂f-1(X∩Y)
∀x∈[f-1(X)∩f-1(Y)]⟹ x∈f-1(X)∧x∈f-1(Y), por definición de unión de conjuntos
⟹f(x)∈X∧f(x)∈Y, por definición de preimagen
⟹f(x)∈(X∩Y), por definición de unión de conjuntos
⟹x∈f-1(X∩Y); por definición de preimagen
∴f-1(X)∩f-1(Y)⊂f-1(X∩Y), por definición de inclusión de conjuntos
∴f-1(X∩Y)=f-1(X)∩f-1(Y), por definición de igualdad de conjuntos∎
- La preimagen del complemento es igual al complemento de la preimagen. Simbólicamente es
Demostrando
Se observa que al igual que en el caso anterior estamos en presencia de una igualdad de conjuntos, así que debemos demostrar la doble inclusión. Procedamos:
i) f-1(X')⊂[f-1(X)]'
∀x∈f-1(X')⟹f(x)∈X', por definición de preimagen
⟹f(x)∉X, por definición de complemento de un conjunto
⟹x∉f-1(X), por definición de preimagen
⟹x∈[f-1(X)]', por definición de complemento de un conjunto
∴f-1(X')⊂[f-1(X)]', por definición de inclusión de conjuntos
ii) [f-1(X)]'⊂f-1(X')
∀x∈[f-1(X)]'⟹x∉f-1(X), por definición de complemento de un conjunto
⟹f(x)∉X, por definición de preimagen
⟹f(x)∈X', por definición de complemento de un conjunto
⟹x∈f-1(X'); por definición de preimagen
∴[f-1(X)]'⊂f-1(X'), por definición de inclusión de conjuntos
∴f-1(X')=[f-1(X)]', por definición de igualdad de conjuntos∎
Las nociones de Imagen y Preimagen en el contexto de las funciones representan conceptos que en general se explican sólo mediante su definición y se pasa a la concreción de las mismas mediante el cálculo porque generalmente lo que interesa es su aplicación en casos concretos, lo cual, no solamente con esta noción sino con muchas otras, reduce el estudio de la Matemática a una perspectiva utilitarista, que en nada favorece la promoción de su estudio en las noveles generaciones. Si bien es cierto, que ser útil al ser humano es una de las aristas más importante de esta ciencia, también es cierto que debe garantizarse su compresión y valoración más allá de los procesos mecanicistas y es allí donde creo que el álgebra como subárea de la misma puede coadyuvar de forma significativa tanto al desarrollo de los procesos de abstracción como al logro de la máxima comprensión.
En este sentido, y como ya es costumbre en mis publicaciones, se enfoca las concepciones de Imagen y Preimagen con la especificidad del caso, a partir de la perspectiva algebraica apoyada en visualizaciones gráficas, lo cual muestra algo diferente a la forma como eventualmente se presentan estos saberes en los textos de Matemática Básica o Cálculo.
En las próximas publicaciones, seguiremos avanzando hacia una temática de estudio diferente, saludos y éxitos para todos los lectores y académicos de esta comunidad.

Para asegurar el estudio de la Matemática por las nuevas generaciones de científicos, la misma ha de ser explicada y promovida desde sus más intrincados y detallados procesos con la mayor claridad posible – Reina Sequera
Para asegurar el estudio de la Matemática por las nuevas generaciones de científicos, la misma ha de ser explicada y promovida desde sus más intrincados y detallados procesos con la mayor claridad posible – Reina Sequera

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia diseñadas en el editor de presentaciones Microsoft Powerpoint 2013, ajustadas y recortadas en Paint.
Publicaciones Relacionadas
Si estás interesado en contenidos sobre Ciencia, Tecnología, Ingeniería y Matemática, consulta las etiquetas #STEM-Espanol y #SteemSTEM, las cuales puedes utilizar para realizar tus publicaciones en esas áreas. Puedes unirte al servidor de Discord de STEM-Espanol para participar en nuestra comunidad y consultar los reportes semanales publicados por @STEM-Espanol. Te esperamos!!
Si estás interesado en contenidos sobre Ciencia, Tecnología, Ingeniería y Matemática, consulta las etiquetas #STEM-Espanol y #SteemSTEM, las cuales puedes utilizar para realizar tus publicaciones en esas áreas. Puedes unirte al servidor de Discord de STEM-Espanol para participar en nuestra comunidad y consultar los reportes semanales publicados por @STEM-Espanol. Te esperamos!!
- Normas STEM-Espanol
- Directrices sobre normas de derechos de autor
- Servidor Discord #STEM-Espanol
- Para unirte al trail de STEM-Espanol
- Vota por @stem.witness como Testigo aquí





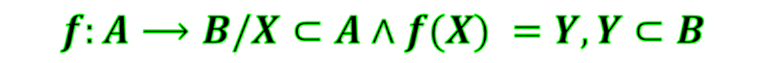
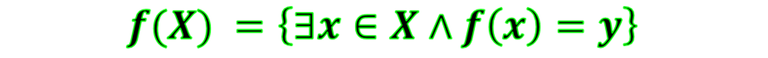
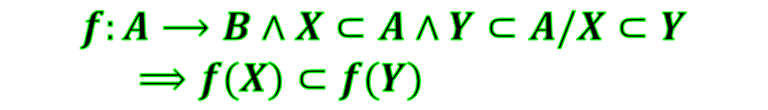
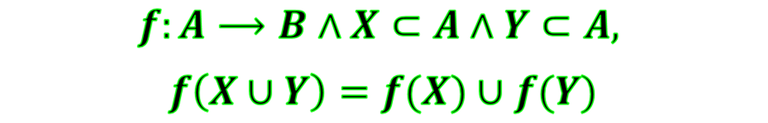
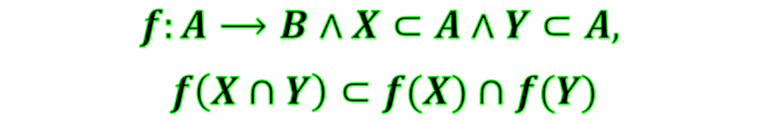
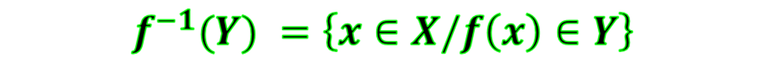
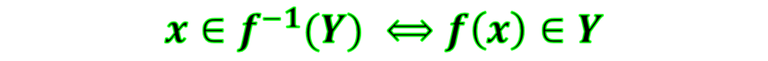
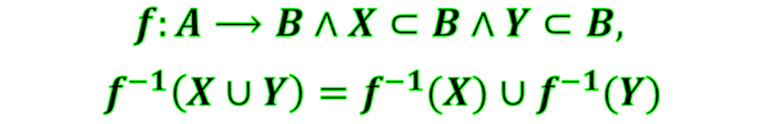
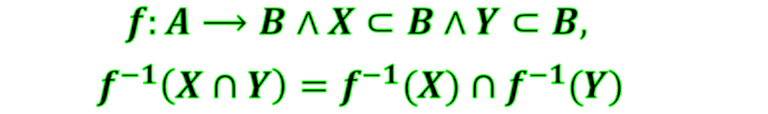
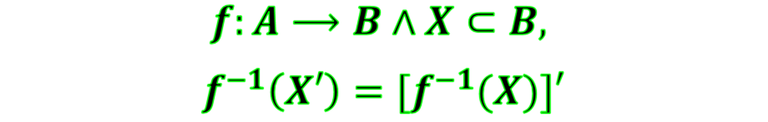

Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
¡Felicidades, #proconocimiento te valoró!
Has sido reconocido(a) por tu buen post por el Comité de Arbitraje y Valoración del Proyecto Conocimiento @proconocimiento.
Apoyamos y valoramos tu esfuerzo...

Proyecto Conocimiento es parte de la comunidad @provenezuela.
Pioneros en la plataforma #steemit en el reconocimiento y valoración a la Producción Intelectual en habla hispana.
Congratulations @reinaseq! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Congratulations @reinaseq! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Muchísimas gracias @rbalzan79, esa es precisamente la búsqueda de los educadores en alguna ciencia específica, presentar los saberes conocidos de tal forma que el estudiante pueda aprender por ellos mismos al leer estas publicaciones, en las mismas tratamos siempre de ser mucho más específicos y detallistas de lo que se presenta en los textos preservando la formalidad del lenguaje matemático, ese precisamente viene a ser nuestro valor agregado!! Gracias por su visita, abrazos fraternos!!
Congratulations @reinaseq! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Congratulations @reinaseq! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @reinaseq! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Congratulations @reinaseq! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard: