
Saludos a la comunidad de Steemiana interesada en los temas matemáticos y científico en general, en la publicación anterior comenzamos a conocer de forma introductoria el saber referido a las Relaciones Binarias haciendo especial énfasis en sus nociones fundamentales, presentándolas en detalle de manera que se pueda comprender la importancia del mismo rumbo al estudio algebraico de las funciones. Asimismo se presentaron argumentos que enfatizan la vinculación del referido concepto en la vida diaria de los seres humanos, a manera de recordatorio
En la realidad humana es posible percibir relaciones entre todo lo que existe de acuerdo a cualidades, propiedades, condiciones, entre otros, que permiten al menos vincular dos situaciones, personas, animales, cosas; es típico en nuestra expresión verbal utilizar frases como
“es amigo de”, “es jefe de”, “vive en”, “obtuvo la calificación”, “su salario es”, “se desempeña en”, “su profesión es”, “se alimenta con”, “es novia de” Fuente
Lo citado nos mantiene en sintonía con el hecho de que las Relaciones Binarias son parte de nuestra habla, nuestra realidad inmediata y en general todo el quehacer humano, se trata de una concepción inevitable en el comportamiento humano.
Adicionalmente, se estableció que éstas se pueden definir en un Producto Cartesiano de dos conjuntos diferentes así como el caso de un mismo conjunto, esto sería decir en símbolos que R⊂A×B o también puede darse el caso de R⊂A×A. Para el caso de relaciones definidas en un conjunto es posible clasificarlas de acuerdo al hecho de si cumplen o verifican algunas propiedades que dotarían a éstas de cualidades especiales y de gran importancia en el ámbito matemático. El conocimiento y comprensión de tales propiedades es el centro de la presente publicación y se detallan en lo sucesivo.

De la misma forma en que es posible definir Relaciones en un Conjunto cualquiera subconjunto del Conjunto Universal asimismo existe la posibilidad de clasificarlas, verificando que las mismas cumplan o no con algunas propiedades, las cuales permiten particularizar tales relaciones con denominaciones específicas (algunas de las cuales se estudiarán en las próximas publicaciones). No obstante, no es obligante ni está garantizado que las cumplan todas a la vez, en todo caso el conocimiento de las mismas nos permite estudiarlas y precisar el alcance de las mismas. En este sentido las propiedades que puede verificar una Relaciones definida en un Conjunto R⊂A×A son:
- Reflexividad
- Simetría
- Transitividad
- Antisimetría
A continuación las conoceremos en detalle una a una. Procedamos:

Esta propiedad nos indica que todo elemento perteneciente al conjunto A está relacionado consigo mismo, esto es que todos pares ordenados de componentes iguales formados a partir de los elementos de A al tiempo que pertenecen al producto cartesiano A×A de igual forma pertenecen a la relación R⊂A×A. Ahora bien, esto nos permite presentar el concepto de Diagonal del producto cartesiano A×A, la cual es un conjunto formado por todos los elementos de A que están relacionados consigo mismo o también se puede decir que es el conjunto de todos los pares ordenados de componentes iguales. En símbolos la Diagonal es
En este sentido, es posible presentar las diferentes alternativas que definen la Reflexividad de una relación R⊂A×A como sigue:
En la primera, la definición alude a la pertenencia de los pares ordenados de componentes iguales, la segunda nos dice que se cumple la reflexividad cuando todo elemento del conjunto está relacionado consigo mismo y la tercera está asociada al concepto de Diagonal. Cuando una relación R⊂A×A es reflexiva se verifican las tres alternativas. Lo indicado se puede visualizar en el siguiente ejemplo:
Dado el conjunto A={a,b,c} y la Relación R={(a,a),(b,b),(c,c),(b,c)} comprobar si es Reflexiva.
Al graficar
En la visualización gráfica nos damos cuenta de que las tres definiciones de la reflexividad se cumplen, esto es, los pares de componentes iguales pertenecen a la relación lo que indica que todo elemento del conjunto A está relacionado consigo mismo y de igual forma la Diagonal del producto cartesiano A×A es subconjunto de R.
Ahora bien, es posible que la reflexidad no se cumpla, es decir, que en una relación dada no se verifique la definición, en este caso se podrían presentar alguna de las siguientes alternativas:
No Reflexividad: Esta opción se da cuando existe algún elemento del conjunto A dado que no está relacionado consigo mismo, o dicho de otra forma que algún par ordenado de componentes iguales no pertenece a la relación, por lo cual también se puede afirmar que la diagonal no es subconjunto de la relación. Simbólicamente tenemos que
Gráficamente sería
Como puede observarse existe un par de la *diagonal que no pertenece a la relación, en consecuencia R es no reflexiva.
Arreflexividad: Esta alternativa es tajante, esto es, ningún elemento del conjunto A está relacionado consigo mismo, por lo cual los pares ordenados de componentes iguales no pertenecen a la relación, por ende, la Diagonal no está incluida en la misma. En símbolos es
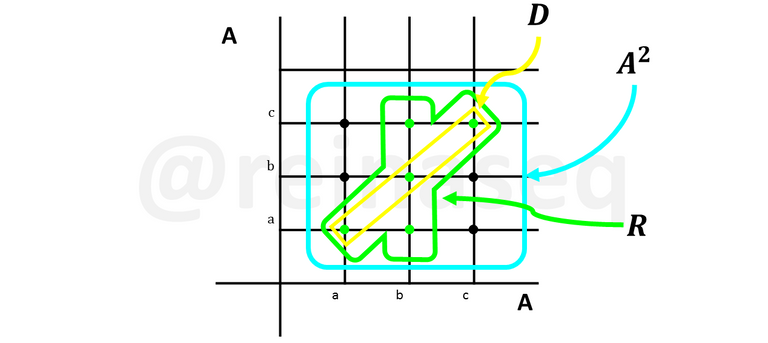
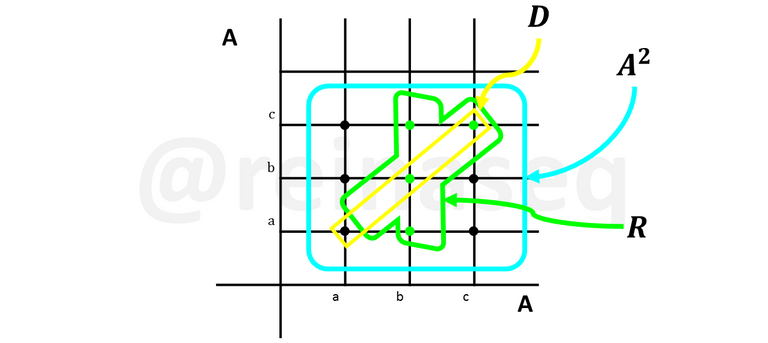
Esto se puede ejemplificar en el siguiente gráfico
En el gráfico puede observarse que ningún elemento de la Diagonal pertenece a la relación, por lo tanto, R es arreflexiva.

En relación a esta propiedad, se afirma que el gráfico debe ser simétrico respecto de la Diagonal, esto es, si una relación la cumple se tiene que si un par ordenado pertenece a R su permutado también debe estar en la misma, vale decir que al referirnos a los pares ordenados que forman parte de la diagonal se dice que son simétricos porque cumplen con la definición, por lo cual se acostumbra a comprobar esta propiedad en los pares ordenados de componentes diferentes. Definiendo formalmente, tendríamos lo siguiente: Dada una relación una relación R⊂A×A se dice que es simétrica si cumple lo siguiente
Visualicemos esta propiedad en el siguiente ejemplo:
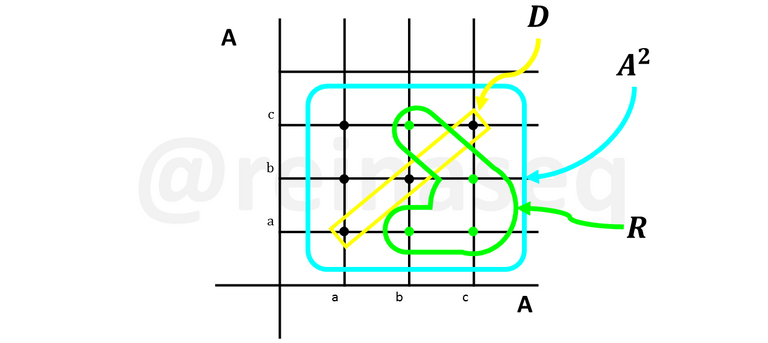
Dado el conjunto A={a,b,c} y la Relación R={(a,a),(b,b),(c,c),(a,b),(b,a)} comprobar si es Simétrica.
Graficando tenemos
Como se puede observar, la relación dada es simétrica al comprobar que (a,b)∈R y su permutado (b,a)∈R. Tal como habíamos indicado, los pares de la diagonal de hecho cumplen con la definición de simetría.
Así como ocurre con la propiedad anterior, es posible que la simetría no se cumpla, hecho que se detalla en dos alternativas que se presentan a continuación:
No Simetría: Para este caso tenemos que puede existir uno o más pares ordenados que estén en la relación pero sus permutados no se encuentran en la misma, esto es, un elemento del conjunto A está relacionado con un segundo pero el segundo no lo está con el primero, de cualquiera de las dos formas se concluye que la relación es no simétrica. Lo afirmado se representa como sigue
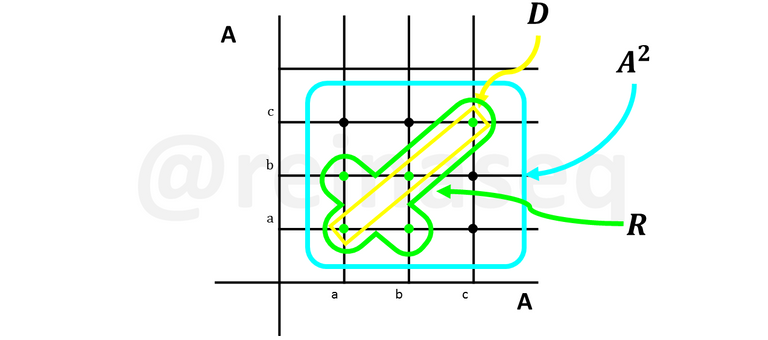
Visualizando en una representación gráfica
Se observa que el par ordenado (b,a)∈R pero su permutado (b,a)∉R, luego la relación R es no simétrica.
Asimetría: Esta alternativa señala que para todos los elementos de A se cumple que si un par ordenado pertenece a la relación su permutado no está en la misma, por lo cual es claro que los pares ordenados de la diagonal no pertenecen a la relación. En símbolos
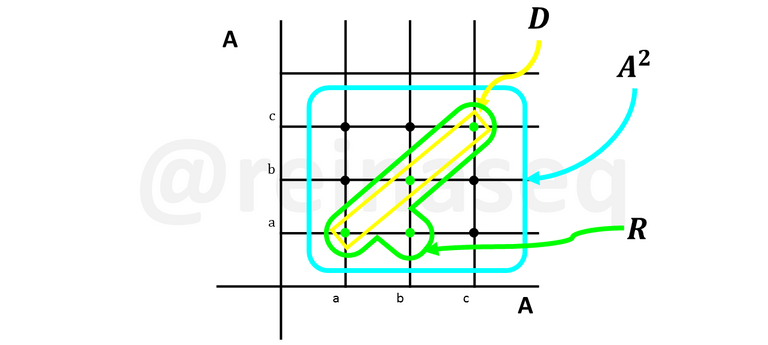
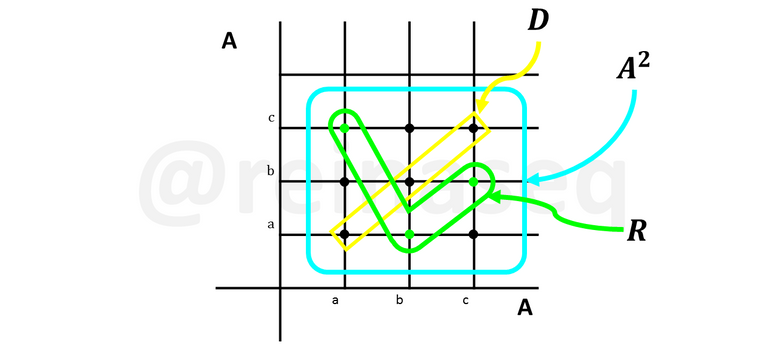
Gráficamente
Se puede apreciar que ningún par ordenado de la diagonal pertenece a la relación y adicionalmente tenemos en los pares ordenados de componentes diferentes que si alguno pertenece a la relación su permutado no está, esto indica que R es asimétrica.

Esta propiedad se requiere al menos tres elementos de un conjunto A cualquiera para establecerla y a partir de allí es posible ampliarla a más elementos. La misma señala que si un elemento está relacionado con un segundo y el segundo relacionado con un tercero se concluye que el primero está relacionado con el tercero. Expresado simbólicamente tenemos
Para el caso de la no transitividad (es decir, cuando no se cumple la propiedad en algunos casos) tenemos la siguiente definición simbólica
Al referirnos a la atransitividad (cuando no se cumple la propiedad en todos los casos) se tiene lo siguiente
Evaluemos esta propiedad y sus alternativas en los ejemplos que se muestran a continuación
- Dada la relación R={(a,a),(b,b),(c,c),(b,c)} comprobar si es Transitiva.
Para evaluar en este caso, es claro que debemos considerar los pares para los cuales se cumpla que la segunda componente del primer par es la primera componente del segundo par tal como lo solicita la definición y luego verificar si hay un par ordenado conformado con la primera componente del primer par y la segunda componente del segundo para poder afirmar que se cumple la transitividad. En efecto, tenemos que (b,b)∈R y (b,c)∈R luego es evidente que el par ordenado (b,c)∈R, por lo cual concluimos que R es transitiva.
- Dada la relación S={(a,b),(b,c),(a,c),(c,a)} verificar si es Transitiva.
En este caso basta con plantear el siguiente contraejemplo, aunque vale destacar que si hay algunos pares transitivos, no obstante
(b,c)∈S y (c,a)∈S pero (b,a)∉S
- Dada la relación T={(a,b),(b,c)} verificar si es Transitiva.
(a,b)∈T y (b,c)∈T sin embargo (a,c)∉T

Esta propiedad establece que si un par y su permutado pertenecen a la relación, las componentes de dichos pares se identifican, esto es, son iguales. Simbólicamente
Esta propiedad sólo admite dos opciones: una relación es o no es antisimétrica, en cuyo caso la posibilidad de no ser se representa como sigue
Analicemos los siguientes ejemplos:
- Dadas las relaciones R={(a,a),(b,b),(c,c),(b,c)} y S={(a,a),(b,c),(c,b)} estudiar en ambos casos la antisimetría.
Para el caso de la relación R nos damos cuenta de que los pares reflexivos cumplen con la definición de antisimetría y el par de componentes diferentes no tiene a su permutado en el conjunto razón por lo cual no se considera para el estudio, luego se concluye que R es antisimétrica.
Ahora estudiemos la relación S, como en ésta sólo hay un par reflexivo que sabemos que si cumple, nos ocuparemos de los pares de componentes diferentes, por lo cual nos damos cuentes de que (b,c)∈S y (c,b)∈S sin embargo b≠c esto nos lleva a concluir que la relación S no es antimétrica.

Hemos estudiado en un nivel teórico comprensivo las Propiedades que se pueden cumplir en una Relación definida en un Conjunto, cada una con alternativas y posibilidades de cumplirse o no, todo dependiendo como esté definida la relación. Esta exposición de saberes es de gran importancia, en tanto que nos van a permitir estudiar y profundizar en casos particulares de gran importancia en este universo algebraico y que eventualmente se estarán publicando y explicando con los detalles del caso. Como es claro, todo conocimiento teórico requiere ejercitación que permita afianzar y dominar adecuadamente para afrontar con éxito los retos académicos futuros, es por ello que la próxima publicación tendrá una connotación práctica para lo cual será necesario tener repasados los conocimientos d ésta y la publicación inmediata anterior.
Nos estamos leyendo en otra oportunidad, saludos y éxitos para todos los lectores y estudiosos de esta comunidad.

Comprender las cosas que nos rodean es la mejor preparación para comprender las cosas que hay más allá - Hipatia de Alejandría.

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia.
Artículo Anterior


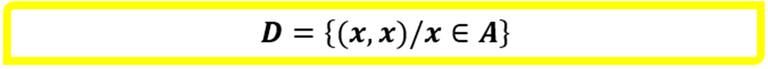


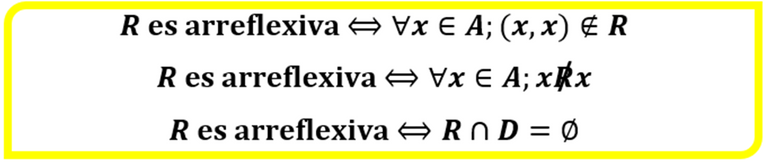
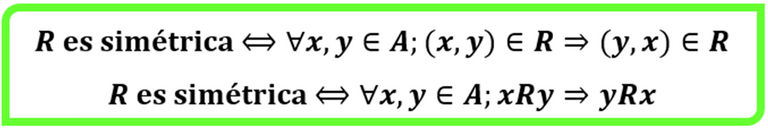

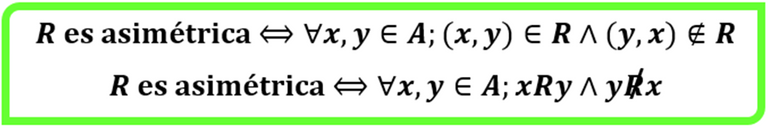
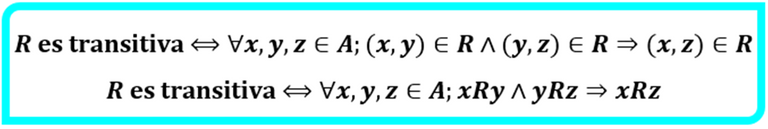
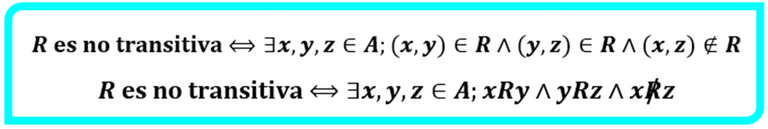
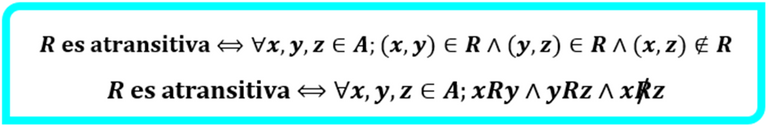
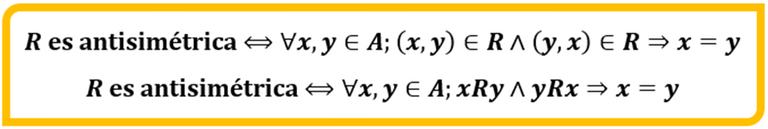
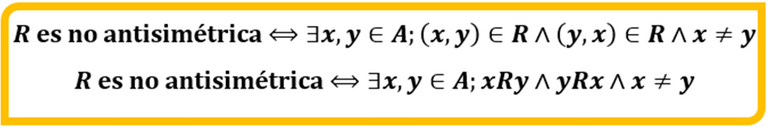
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Thank you, I am very happy and grateful for such important support, they are great!
Agradecida con tu aporte @eniolw, cada comentario de este tipo enriquece las publicaciones que hacemos y los autores aprendemos e intercambiamos con otros expertos!! Abrazos!!
Muchísimas gracias por el apoyo, grandes abrazos para ustedes!!