Saludos a todos los lectores de la comunidad de Steemit, en esta oportunidad les presentaré el inicio de una nueva temática propia del Álgebra Abstracta y tan interesante y apasionante como los temas presentados en anteriores publicaciones, se trata de las Relaciones Binarias las cuales en general se mencionan someramente en el universo matemático antes de pasar a las Funciones, sin embargo, los interesados suelen sumergirse en las profundidades, reconociendo la importancia que tienen tanto en el escenario de la Matemática como de nuestra vida diaria, en la cual solemos utilizarlas de forma muy frecuente sin darnos cuenta de que lo hacemos.
En la realidad humana es posible percibir relaciones entre todo lo que existe de acuerdo a cualidades, propiedades, condiciones, entre otros, que permiten al menos vincular dos situaciones, personas, animales, cosas; es típico en nuestra expresión verbal utilizar frases como
“es amigo de”, “es jefe de”, “vive en”, “obtuvo la calificación”, “su salario es”, “se desempeña en”, “su profesión es”, “se alimenta con”, “es novia de”,
entre muchas otras, razón por la cual observamos que uno de los saberes matemáticos más habituales es precisamente el que presentamos en esta oportunidad. Ahora que ya hemos introducido intuitivamente las Relaciones Binarias corresponde definir de manera formal el referido concepto.
Dados dos conjuntos A⊂U y B⊂U dos conjuntos cualesquiera y una propiedad P(x,y) que permite vincular los elementos x∈A y y∈B en ese orden. Ahora bien, consideremos el Producto Cartesiano A×B, el cual por su definición está conformado por pares ordenados (a,b), luego la relación R se define de la siguiente manera
En este sentido podemos plantearnos el siguiente ejemplo: Supongamos que tenemos un conjunto A conformado por letras que identifican hombres y un conjunto B integrado por letras que identifican mujeres como sigue
A={a,b,c,d}
B={x,y,z,w}
Se puede plantear una propiedad P(x,y) que vincula los elementos de dichos conjuntos tal como “es amigo de”. Es claro que entre los conjuntos dados se genera un Producto Cartesiano A×B, sin embargo, no todos los pares ordenados de dicho conjunto cumplen con la propiedad indicada (esto podría ser bien sea porque las personas involucradas no se conocen o porque apenas son conocidos).
El conjunto que define el Producto Cartesiano A×B representado por extensión es
A×B={(a,x),(a,y),(a,z),(a,w),(b,x),(b,y),(b,z),(b,w),(c,x),(c,y),(c,z),(c,w),(d,x),(d,y),(d,z),(d,w)}
La relación R⊂A×B podría ser
R={(a,x),(a,w),(b,x),(b,y),(d,z)}
Esto indica que sólo los pares ordenados que pertenecen a la relación R⊂A×B satisfacen la propiedad P(x,y) “es amigo de” dada.
Desde la perspectiva gráfica, las Relaciones Binarias pueden ser representadas de tres formas posibles: Diagrama de Venn (ya conocida en anteriores publicaciones), Gráfico Cartesiano y Matriz. A continuación se explica y muestra cada uno:
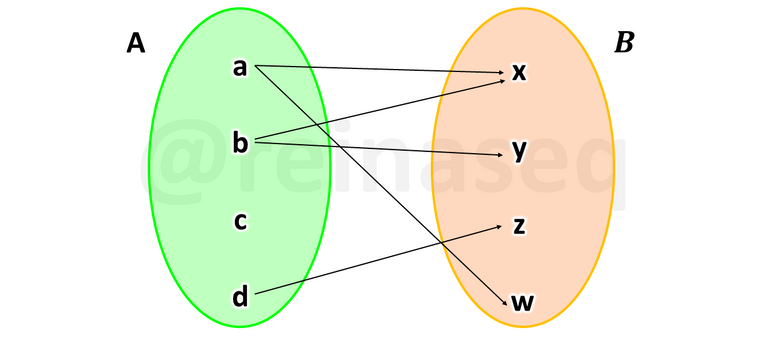
- Diagrama de Venn: En esta representación generalmente se dibujan dos formas ovaladas una al lado de la otra las cuales representan la de la izquierda el primer conjunto o de partida y la de la derecha el segundo conjunto o de llegada, en cada uno en su interior se escriben los elementos que pertenecen a los mismos en detalle, adicionalmente, del primero se acostumbran a dibujar flechas que salen de los elementos de éste hacia los del otro conjunto siempre y cuando los mismos estén vinculados o relacionados. Lo dicho puede visualizarse en la siguiente imagen en la cual se ilustra lo referido al ejemplo dado anteriormente
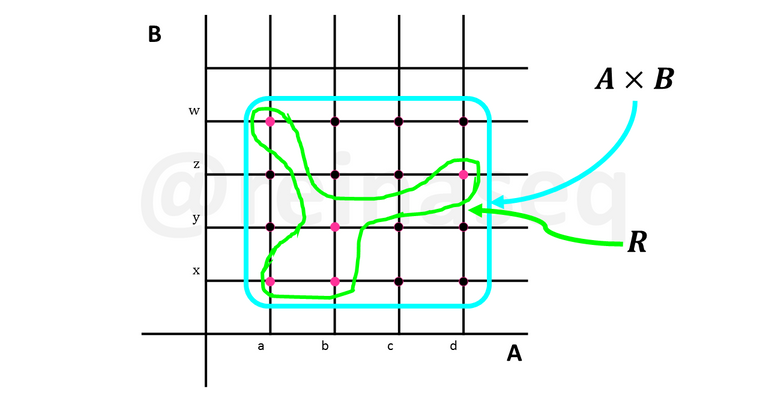
- Gráfico Cartesiano: Esta representación es muy conocida en el ámbito de la Matemática, la misma consiste en la intersección en el plano de dos ejes mutuamente perpendiculares (es decir, entre sí forman ángulos de 90 grados), de los cuales el eje horizontal se le denomina eje de las abscisas y en él se ubican los elementos del primer conjunto y el vertical se conoce como eje de las ordenadas en el cual se sitúan los elementos del segundo conjunto. Posteriormente, se trazan paralelas de cada uno de los elementos representados en los ejes lo cual forma cuadrícula, de la misma los diferentes vértices que unen los elementos de los conjuntos dados son los pares ordenados que forman parte del Producto Cartesiano entre los mismos. De este, se destacan de alguna forma particular los elementos o pares que integran la relación R. La representación sería como se muestra a continuación
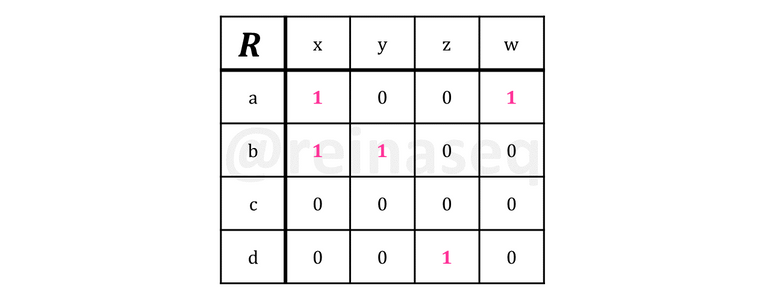
- Matriz: En esta forma, se acostumbra a dibujar una tabla de doble entrada ubicando en la primera columna de la izquierda los elementos del primer conjunto y en la fila superior los elementos que pertenecen al segundo conjunto. En el primer recuadro ubicado en la esquina superior izquierda se escribe la relación o propiedad que permitirá vincular los elementos de los conjuntos dados. A continuación se procederá a llenar los recuadros interceptores entre elementos de la siguiente manera: se escribirá cero “0” si no están relacionados y uno “1” si en efecto hay relación entre los mismos. A continuación se muestra la representación de esta forma gráfica
Por lo general, no todos los elementos de los conjuntos dados están relacionados sino algunos de ellos, en este sentido, se acostumbra representar los mismos en dos importantes conjuntos denominados Dominio de una Relación donde estarán los elementos del conjunto de partida que pertenecen a la relación e Imagen de una Relación en el cual se encontrarán los elementos del conjunto de llegada que forman parte de la relación. Matemáticamente hablando, se definen como sigue
Dados dos conjuntos cualesquiera A⊂U y B⊂U y una relación R⊂A×B se tiene que
Para el caso del ejemplo que se desarrolla en este trabajo tendríamos que los conjuntos Dominio e Imagen de una Relación de acuerdo a las definiciones dadas serían los siguientes
Si la relación R se define en el Producto Cartesiano A×B, su Relación Inversa se define en sentido contrario considerando como conjunto de partida a B y como conjunto de llegada a A, esto indica que
Y se define de la siguiente forma
En sintonía con la definición y considerando nuestro ejemplo, la Relación Inversa sería el siguiente conjunto
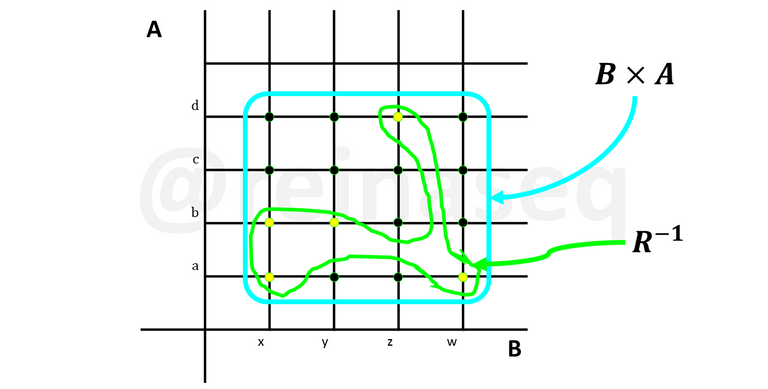
Claro está, como recordamos la relación R es la propiedad “es amigo de”, sin embargo, en el caso de la inversa, los conjuntos se intercambian y dado que el conjunto A dado es de hombre y el B es de mujeres, la propiedad de la relación inversa sería “es amiga de”. Su representación gráfica es
En ocasiones, los elementos de un conjunto de partida pueden estar conectados por más de una relación, como generalmente sucede en la cotidianidad. Para el caso de nuestro ejemplo una segunda propiedad podría ser “su salario es”, esto indica que cuando los elementos van de un primer conjunto a un segundo la característica que los vincula sería “es amigo de” y cuando van de un segundo a un tercero sería la que acabamos de precisar.
Ahora bien, esto es posible prolongarlo estableciendo otras propiedades hasta que no haya elementos que relacionar. Lo dicho, nos indica que se pueden componer relaciones con otras, lo que da cabida a definir matemáticamente esta concepción como sigue
En la Composición de Relaciones se verifican dos importantes propiedades
La primera es la Asociatividad
La segunda es: la relación inversa de la composición de relaciones es igual a la composición de relaciones inversas en orden permutado, como se escribe a continuación
Las mismas serán demostradas en posteriores publicaciones. En lo que respecta a nuestro ejemplo recordemos lo siguiente
A={a,b,c,d}
B={x,y,z,w}
C={1,2,3} (El conjunto adicional necesario para poder referirnos a una Composición de Relaciones)
R={(a,x),(a,w),(b,x),(b,y),(d,z)}
S={(x,1),(x,2),(w,3)} (Relación adicional por extensión)
Por definición, para que un elemento pertenezca a la relación compuesta debe poder transitar desde el primer conjunto al tercer conjunto, en el caso de nuestro ejemplo quedaría
S∘R={(a,1),(a,2)}
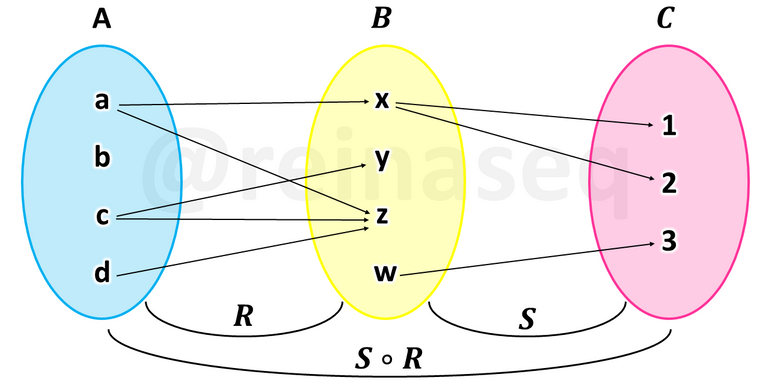
La Relación Compuesta se representa gráficamente como se muestra a continuación
Como se ha indicado anteriormente, una Relación Binaria puede definirse entre conjuntos iguales o diferentes, en este sentido ya nos hemos referido genéricamente a relaciones definidas en conjuntos diferentes, para el caso de conjuntos iguales valen las definiciones y propiedades anteriormente mencionadas, bajo las siguientes condiciones
Sea R⊂A×B en la cual A=B, al ser iguales los conjuntos nuestra relación estaría definida así
Lo que indica que la relación dada está definida sobre el mismo conjunto. Ahora bien, todos los posibles subconjuntos del Producto Cartesiano A×A se consideran posibles relaciones definidas en el mismo, para lo cual existen dos casos triviales: el conjunto vacío y el mismo A×A.
Adicionalmente, para conocer todas las posibles relaciones definidas en A×A se estima de la siguiente forma: Si el conjunto A dado posee n elementos entonces
Como ejemplo, podríamos tener lo siguiente:
Dado A={a,b} identificar todas las posibles relaciones que son subconjunto del Producto Cartesiano A×A.
Solución:
Si el conjunto A tiene 2 elementos el Producto Cartesiano A×A tendrá 4 elementos como se muestra a continuación:
A×A={(a,a),(a,b),(b,a),(b,b)}
Las mismas se especifican a continuación:
En la próxima publicación estaré ampliando y detallando otros aspectos de la temática Relaciones Binarias, nos leemos.

“No podemos enseñar nada a nadie. Tan sólo podemos ayudar a que descubran por sí mismos” - Galileo Galilei .

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia.
Artículo Anterior








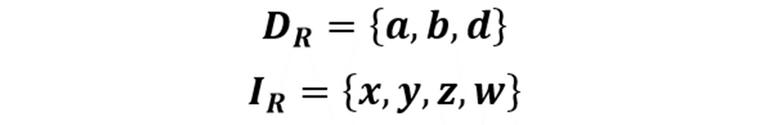

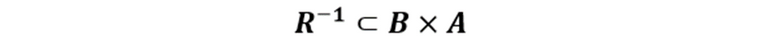
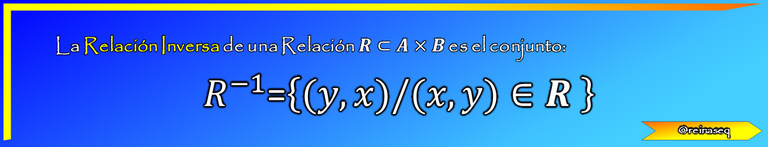
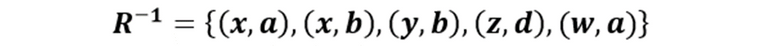

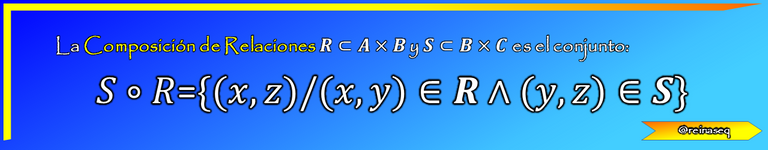
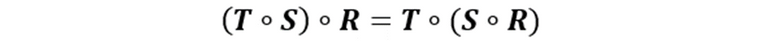
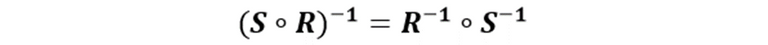

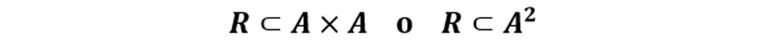
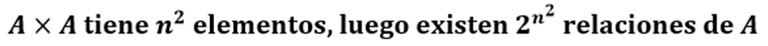


Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.