
Saludos a toda la comunidad de Steemiana, en esta oportunidad dando continuidad a la temática relativa a las Relaciones Binarias se estará desarrollando en detalle lo concerniente a las Relaciones de Equivalencia, concepto de gran importancia en el ámbito de la Matemática en tanto que le dan soporte teórico a nociones de mayor complejidad en el referido escenario, tales como, la existencia de conjuntos numéricos conocidos (los cuales no existen a capricho, sino que tienen su razón de ser debidamente justificada) y en este sentido como es el caso de todo conocimiento matemático, se pierden de vista los escenarios en los cuales están presentes directa o indirectamente esta concepción.
Para poder tener una fácil comprensión de los aspectos que se presentarán a continuación es necesario revisar las publicaciones anteriores de este blog vinculadas al tema las cuales estarán disponibles al final de este post a través de enlaces directos a las mismas.

Sea la relación R⊂A×A, la misma será de equivalencia si y sólo si cumple con las siguientes propiedades: Reflexividad, Simetría y Transitividad. En el caso de las relaciones de equivalencia, para denotar que dos elementos cualesquiera están relacionados se utiliza el símbolo ~ lo cual transforma la notación habitual aRb en a~b que se lee a y b son equivalentes o también a es equivalente a b, luego se puede afirmar que el par ordenado (a,b) pertenece a la relación.
En símbolos se expresa la definición como sigue
La notación a~b permite expresar las propiedades como sigue
Ejemplo
Dados el conjunto A={a,b,c} y la relación R={(a,a),(b,b),(c,c),(a,b),(b,a)} verificar si R es una relación de equivalencia
Solución
Para dar respuesta al planteamiento se debe comprobar si se cumple la definición de relación de equivalencia, esto es, se debe investigar si se cumplen las propiedades de Reflexividad, Simetría y Transitividad. Procedamos:
Reflexividad: Como se puede observar en el conjunto dado, todos los elementos de A={a,b,c} están relacionados consigo mismo, esto es: a~a, b~b y c~c, luego se puede afirmar que la relación R es reflexiva.
Simetría: En este caso, debemos recordar que los pares reflexivos son simétricos, luego comprobaremos la definición en los pares de componentes diferentes como sigue
(a,b) y (b,a) pertenecen a la relación, por consiguiente se cumple que si a~b⇒b~a lo que indica que la relación R es simétrica por definición.
Transitividad: en relación a esta propiedad procederemos con las siguientes comprobaciones
a~a∧a~b⇒a~b
a~b∧b~a⇒a~a
b~a∧a~b⇒b~b
a~a∧a~a⇒a~a
Como se puede evidenciar las proposiciones son verdaderas, esto nos lleva a afirmar que R es transitiva.
Una vez comprobadas las propiedades y darnos cuentan que todas se cumplen concluidos que R es ∼ y se lee R es una relación de equivalencia y el conjunto dado se puede expresar como sigue
∼={(a,a),(b,b),(c,c),(a,b),(b,a)}
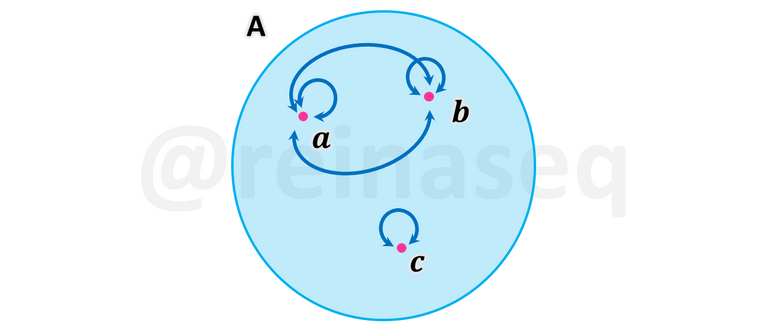
Gráficamente se representa de la siguiente manera
Diagrama de Venn
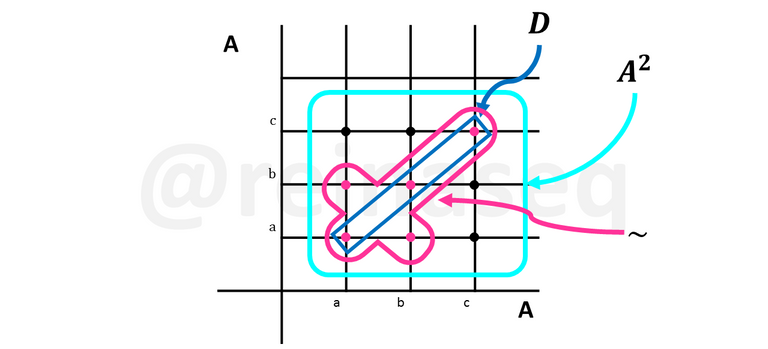
Gráfico Cartesiano

Al definir en un conjunto A cualquiera una relación y demostrar que la misma es de equivalencia, el referido conjunto se subdivide en ciertos subconjuntos los cuales tienen como elementos todos aquellos que son equivalentes con un determinado x∈A, tales subconjuntos se denominan clases de equivalencia y se definen matemáticamente de la siguiente forma
Sea el conjunto A y una relación de equivalencia ~ definida en dicho conjunto, la clase de equivalencia de un cierto elemento a∈A es en conjunto formado por todos los elementos que son equivalentes a él, lo cual se expresa en símbolos como sigue
Esto quiere decir que
En el caso del ejemplo que venimos desarrollando el conjunto A={a,b,c} tendría dos relaciones de equivalencia que se expresan como sigue
Gráficamente
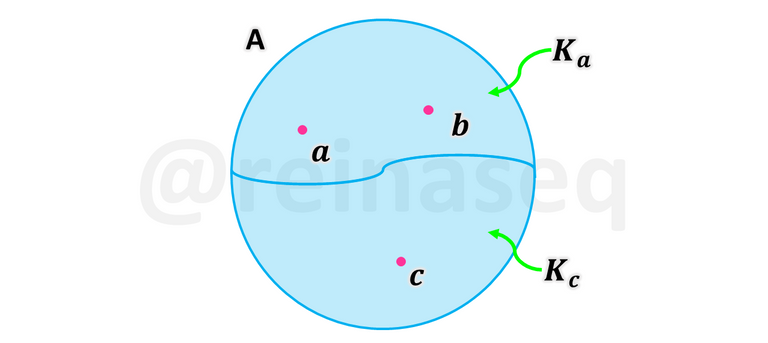
Ahora bien, en este momento nos damos cuenta que se estarían generando muchos subconjuntos de A de acuerdo a la definición anterior, lo cual nos lleva a un conjunto importante que estaría agrupando a todas las clases de equivalencia generadas el cual se denomina Conjunto Cociente de A. Adicionalmente, se estarán generando i clases de equivalencia por lo cual conviene tener en cuenta un conjunto de índices que tendrá la misma cantidad de elementos que clases generadas. Simbólicamente, el Conjunto Cociente de A quedaría representado como sigue
Es importante destacar que el elemento u∈I que identifica la clase de equivalencia se le denomina elemento canónico el cual representa el elemento más pequeño de la clase, es decir, si se tratase de números sería el menos de ellos y si son letras se considera la más inicial en relación a la secuencia del alfabeto.
Con el propósito de ampliar y comprender mejor estas nociones se realizará el estudio respectivo a la relación congruencia módulo n para lo cual en principio es conviene conocer cómo está definida y otros enunciados y propiedades vinculadas, luego procederemos a demostrar si la misma es una relación de equivalencia, en caso de serlo hallaremos las clases de equivalencia y el conjunto cociente.

La relación congruencia módulo n se define como sigue:
Sea R una relación definida en el conjunto de los números enteros Z, se dice que dos elementos con congruentes módulo n si y sólo si n es divisor de la diferencia de dichos elementos. Expresado en símbolos tenemos
Adicionalmente, se tiene que un número natural n cualquiera es divisor de un cierto número entero x si y sólo sí el entero es el resultado de multiplicar n por otro número entero k. En símbolos
Con respecto a la relación divisor de se presentan a continuación sus propiedades:
- Si un número natural n cualquiera divide a un número entero, entonces también divide al producto de éste por cualquier otro entero, esto es
- Si un número natural n cualquiera divide a otros dos números enteros, implica que también divide a la suma o diferencia de los mismos. En símbolos
- Si un número natural n cualquiera divide a un número entero cualquiera, también divide a su opuesto. Simbólicamente es
(La demostración de estas propiedades se desarrollarán en posteriores publicaciones).
Una vez que se conocen los aspectos teóricos inherentes a la relación congruencia módulo n, procederemos a demostrar si se trata de una relación de equivalencia, en caso de serlo, se determinarán sus clases de equivalencia y el respectivo conjunto cociente. Consideremos lo siguiente
Para demostrar si se trata de una relación de equivalencia debemos verificar si se cumplen las propiedades de reflexividad, simetría y transitividad de acuerdo a la definición.
Reflexividad:
∃0∈Z/n|0, por propiedad de la multiplicación en el conjunto de los números enteros Z
⟹n|a+(-a), por definición de elemento opuesto en el conjunto de los números enteros Z
⟹n|a-a, por convenio de notación x-x=x+(-x), ∀x∈Z
⟹ a es congruente con a módulo n, por definición de la relación congruencia módulo n
⟹ a~a, por definición i
∴ La relación congruencia módulo n es Reflexiva, por definición de reflexividad.
Simetría:
∀a,b∈Z,n∈N,a~b⟹n|a-b, por definición de la relación congruencia módulo n y definición i
⟹n|a+(-b), por convenio de notación x-x=x+(-x), ∀x∈Z
⟹n|-[a+(-b)], por propiedad 3 de la relación divisor de
⟹n|-a+b, por propiedad distributiva en el conjunto de los números enteros Z y regla de los signos para la multiplicación en el conjunto de los números enteros Z
⟹n|b+(-a), por propiedad conmutativa de la adición en el conjunto de los números enteros Z
⟹n|b-a, por convenio de notación x-x=x+(-x), ∀x∈Z
⟹b~a, por definición de la relación congruencia módulo n y definición i
∴ La relación congruencia módulo n es Simétrica, por definición de simetría.
Transitividad:
∀a,b,c∈Z,n∈N,a~b∧ b~c⟹n|a-b∧n|b-c, por definición de la relación congruencia módulo n y definición i
⟹n|(a-b)+(b-c), por propiedad 2 de la relación divisor de
⟹n|[a+(-b)]+[b+(-c)], por convenio de notación x-x=x+(-x), ∀x∈Z
⟹n|a+[(-b)]+b]+(-c), por propiedad asociativa de la adición en el conjunto de los números enteros Z
⟹n|(a+0)+(-c), por definición de elemento opuesto en el conjunto de los números enteros Z
⟹n|a+(-c), por definición de elemento neutro de la adición en el conjunto de los números enteros Z
⟹n|a-c, por convenio de notación x-x=x+(-x), ∀x∈Z
⟹a~c, por definición de la relación congruencia módulo n y definición i
∴ La relación congruencia módulo n es Transitiva, por definición de transitividad.
∴ La relación congruencia módulo n es una relación de equivalencia, por definición de relación de equivalencia.
Ya hemos demostrado que la relación congruencia módulo n es una relación de equivalencia, por lo cual se procederá a determinar las clases de equivalencia y el conjunto cociente respectivos.
Clases de Equivalencia
Para precisar las clases de equivalencia de la relación congruencia módulo n es necesario considerar ambas definiciones como sigue
Si aplicamos la definición de la relación congruencia módulo n tenemos
x~a⟹n|x-a, por definición de la relación congruencia módulo n y definición i
⟹x-a=n.k,k∈Z, por definición de la relación divisor de
⟹x+(-a)=n.k, por convenio de notación x-x=x+(-x), ∀x∈Z
⟹x+[(-a)+a]=n.k+a, sumando a a derecha en ambos miembros de la igualdad y por propiedad asociativa de la adición en el conjunto de los números enteros Z
⟹x+0=n.k+a, por definición de elemento opuesto en el conjunto de los números enteros Z
⟹x=n.k+a, por definición de elemento neutro de la adición en el conjunto de los números enteros Z
⟹x=a+n.k, por propiedad conmutativa de la adición en el conjunto de los números enteros Z
Lo anterior indica que las clases de equivalencia vienen dadas por la suma del elemento a∈Z con los múltiplos de n. Representando algunos casos por extensión tenemos lo siguiente
Los subíndices de las clases de equivalencia son los posibles restos de la división de un entero por n, es decir: 0, 1, 2, …, n-1, lo cual tiene plena justificación por el algoritmo de la división entera, esto indica que el resto es positivo y menor que el divisor. En este sentido las clases de equivalencia obtenidas reciben el nombre de clases de restos módulo n y suelen representarse como sigue
Esto quiere decir que el conjunto cociente viene dado por
De igual manera puede expresarse
O también
Es evidente que las clases de equivalencia son diferentes del conjunto vacío, disjuntas entre si dos a dos y la unión de todas nos resulta el conjunto de los números enteros Z.

La primera condición nos indica que las clases de equivalencia deben ser diferentes del conjunto vacío, en cuanto a la segunda es claro que las clases no pueden tener elementos en común por lo cual éstas son disjuntas, y en cuanto a la tercera nos señala que la unión de todas las clases de equivalencia nos da como resultado el conjunto A.

En esta oportunidad hemos estudiado y comprendido en concepto referente a las Relaciones de Equivalencia y nociones inherentes tales como las clases de equivalencia, el conjunto cociente y la partición de un conjunto no vacío, además hemos evidenciado en un caso concreto tales aspectos teóricos, en el caso específico de la relación congruencia módulo n, esto nos ha permitido evidenciar que tales aplicaciones ha derivado en conceptualizaciones matemática de gran importancia en ese ámbito y que encuentran soporte teórico en lo presentado en esta publicación.
En las próximas publicaciones, estaré ampliando otras conceptualizaciones vinculadas a las relaciones de equivalencia, de igual manera se mostrará otros ejemplos que permitirán visualizar otras derivaciones matemáticas que se dan a partir de las mismas. Esta temática es realmente fascinante, espero que se sigamos haciendo el seguimiento a lo que viene que de seguro será de gran deleite para los amantes de la Matemática.
Nos leemos en la siguiente publicación, saludos y éxitos para todos los lectores y estudiosos de esta comunidad.

“Aprende todo lo necesario para que tu vida sea más feliz” - Pitágoras.

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia diseñadas en el editor de presentaciones Microsoft Powerpoint 2013, ajustadas y recortadas en Paint.
Publicaciones Relacionadas





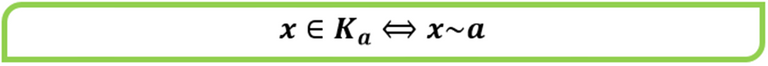
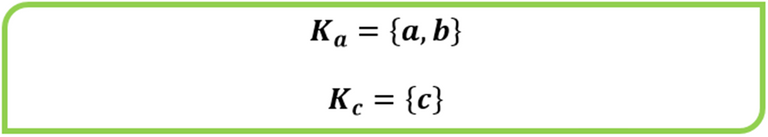
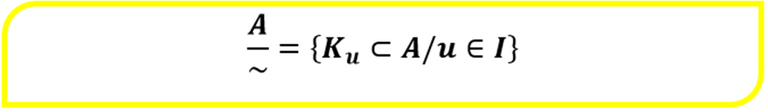

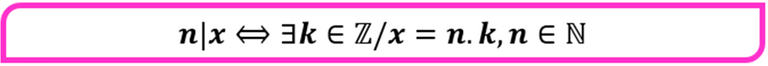

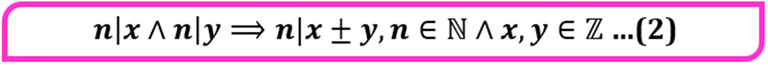
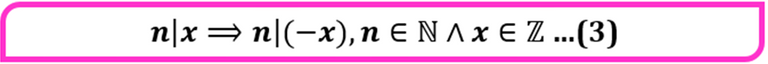
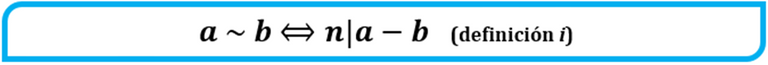
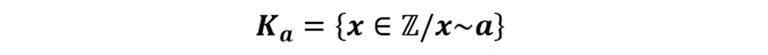

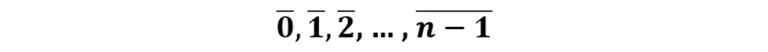
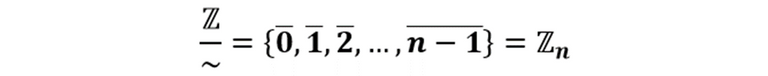
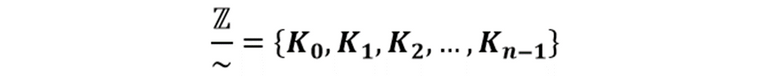
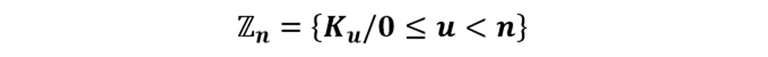

This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Wonderful, very grateful for the support, great hugs!!
Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Canal Discord ¡Te esperamos!Votado por el trail @team-mexico
Delegaciones para @team-mexico ¡Ayúdanos a crecer!
10 SP - 25 SP - 50 SP - 100 SP - 150 SP- Mas información.
.png)
Saludos y abrazos, gracias por el apoyo!!
posts sobre teoría de conjuntos. Saludos!Hola @ReinaSeq. Qué bueno que sigues con esta serie de
Hola @eniolw, la temática como sabrás es extensa y muy interesante, gracias por el seguimiento!! Saludos!!