
Saludos a toda la comunidad de Steemiana, en esta oportunidad en el marco de la temática relativa a las Relaciones Binarias y ya cerrando este emocionante capítulo de la Matemática, se presenta el tópico Relaciones de Orden, para el cual es de gran importancia tener presente los saberes compartidos en la publicación titulada Propiedades de las Relaciones definidas en un Conjunto.
En este sentido, antes de adentrarnos a los conceptos propiamente matemáticos, es pertinente reflexionar acerca de la noción de orden, en tanto que nos damos cuenta que la misma está íntimamente involucrada con el quehacer cotidiano del ser humano quien de manera natural siempre anda en la búsqueda de clasificar tanto objetos, animales, personas, así como los procesos humanos en general. Tal categorización generalmente se corresponde con criterios descendentes o ascendentes, es decir, lo que predomina en mayor o menor grado en los aspectos de interés de los individuos, tanto objetivos como subjetivos, los cuales serán ampliados en la presente publicación. Los invito a leer detalladamente la información que a continuación se presenta, con sentido reflexivo.

Como se ha indicado en las ideas previas, el ser humano tiene una notable tendencia a ordenar los elementos con los cuales interactúa en la cotidianidad, en general lo realiza considerando los aspectos que están antes de y luego los que suceden después de lo cual nos da la idea de orden cronológico. Asimismo, se tiende a clasificar los de menor valoración hasta los que tienen mayor valor, hecho que a manera de ejemplo nos invita a pensar en la noción de antecedente o precedente y consecuente o sucediente. Desde el punto de vista matemático, el orden se expresa genéricamente mediante el término preceder para indicar que ciertos elementos preceden a otros. Luego, cuando se afirma que un cierto x precede a y lo que se quiere indicar es que el par ordenado (x,y)∈R.
Es de hacer notar, que en el caso de las Relaciones de Orden la propiedad transitiva es fundamental considerándose la columna vertebral de esta noción, no obstante, el cumplimiento o no de otras propiedades permite distinguir los siguientes tipos de Relaciones de Orden
- Orden Amplio
- Orden Estricto
A continuación se detallarán las definiciones en cada caso.

Sea la relación R⊂A2, se dice que R es una relación de orden amplio en el conjunto A si y sólo sí cumple con las propiedades de reflexividad, antisimetría y transitividad, lo cual se expresa en símbolos como sigue
Las relaciones de orden amplio se clasifican a su vez en
- Orden Parcial
Una relación será de orden parcial si y sólo si existen pares de elementos incomparables. Esto es
- Orden Total
Una relación será de orden total si y sólo si existen pares de elementos comparables. En símbolos
Lo anterior nos indica que cuando se demuestra que una relación es de orden amplio en general, de forma adicional se debe comprobar si la misma es de orden parcial o total. A continuación se presentan ejemplos para ampliar estas concepciones.
Ejemplo 1:
En el conjunto de los números naturales N se define la relación divisor de, estudiar el tipo de orden que se verifica.
Solución
La relación R se define así
Recordemos como está definida la relación divisor de,
Lo primero que debemos comprobar es la definición de orden amplio, por lo cual procederemos a verificar las propiedades de reflexividad, antisimetría y transitividad.
- Reflexividad:
∀a∈N⟹a=a.1, por definición de elemento neutro para la multiplicación en el conjunto de los números naturales N
⟹a|a, por definición de la relación divisor de
⟹(a,a)∈R, por definición de la relación R
∴ La relación divisor de es Reflexiva, por definición de reflexividad.
- Antisimetría:
∀a,b∈N,a|b∧b|a⟹∃n,m∈N∧b=a.n∧a=b.m, por definición de la relación divisor de
⟹a=b.m∧b=a.n, ley lógica conmutativa de la conjunción
⟹a.b=(b.m).(a.n), multiplicando miembro a miembro
⟹a.b=(a.n).(b.m), por propiedad conmutativa de la multiplicación en el conjunto de los números naturales N
⟹a.b=a.(n.b).m, por propiedad asociativa de la multiplicación en el conjunto de los números naturales N
⟹a.b=a.(b.n).m, por propiedad conmutativa de la multiplicación en el conjunto de los números naturales N
⟹a.b=(a.b).(n.m), por propiedad asociativa de la multiplicación en el conjunto de los números naturales N
⟹a.b.1=(a.b).(n.m), por definición de elemento inverso en el conjunto de los números naturales N
⟹1=n.m, por propiedad cancelativa en el conjunto de los números naturales N
⟹n=1∧m=1, para que el producto de dos elementos sea 1 ambos deben ser iguales a 1
⟹n=1∧1=m, por simetría de la igualdad
⟹n=m, por transitividad de la igualdad
Retomando
a=b.m∧b=a.n⟹a=b.1∧b=a.1, por comprobación previa
⟹a=b∧b=a, por definición de elemento neutro para la multiplicación en el conjunto de los números naturales N
⟹a=b∧a=b, por simetría de la igualdad
⟹a=b, por ley lógica de idempotencia de la conjunción
∴ La relación divisor de es Antisimétrica, por definición de antisimetría.
- Transitividad:
∀a,b,c∈N,a|b∧b|c⟹∃n,m∈N∧b=a.n∧c=b.m, por definición de la relación divisor de
⟹b.c=(a.n).(b.m), multiplicando miembro a miembro
⟹b.c=(b.m).(a.n), por propiedad conmutativa de la multiplicación en el conjunto de los números naturales N
⟹c=m.(a.n), por propiedad cancelativa de la multiplicación en el conjunto de los números naturales N
⟹c=a.(n.m), por propiedades conmutativa y asociativa de la multiplicación en el conjunto de los números naturales N
⟹c=a.k, k=n.m, por clausura de la multiplicación en el conjunto de los números naturales N
⟹a|c, por definición de la relación divisor de
⟹(a,c)∈R, por definición de la relación R
∴ La relación divisor de es Transitiva, por definición de transitividad.
∴ La relación divisor de es de orden amplio, por definición de relación de orden amplio.
Ahora bien, recordemos que la relación está definida en el conjunto de los números naturales N, por lo cual mediante un simple contraejemplo se puede afirmar que la misma es de orden amplio y parcial en tanto que es falso que 5|4 ∨ 4|5.
Por otro lado, se puede afirmar que si la relación se define en el conjunto de los números enteros Z, no se cumpliría la propiedad antisimétrica, por lo cual no se verificaría el orden amplio.
Ejemplo 2:
Dado el conjunto A={a,b,c} y la relación S={(a,a),(b,b),(c,c),(a,b),(a,c),(b,c)}, estudiar el orden de S.
Solución
Como se puede apreciar, la relación es reflexiva en tanto que la Diagonal está contenida en la relación S, esto indica que todos los elementos del conjunto A están relacionados consigo mismo. En el caso de la asimetría observamos que los pares reflexivos cumplen con la propiedad y en el caso de los pares ordenados de componentes diferentes no se estudia ya que los pares permutados no pertenecen a la relación, esto implica que la misma es antisimétrica. Finalmente, para la transitividad se tiene que
aSa∧aSb⇒aSb
aSa∧aSc⇒aSc
bSb∧bSc⇒bSc
aSb∧bSc⇒bSc
Analizando las diferentes alternativas nos damos cuenta de que S es transitiva, por lo tanto se puede afirmar que la relación es de orden amplio.
Adicionalmente, nos damos cuenta de que S es de orden total ya que existen pares de elementos comparables tal como indica la definición.
∴ La relación S es de orden amplio y total

Sea la relación R⊂A2, se tiene que R es una relación de orden estricto en el conjunto A si y sólo sí cumple con las propiedades de arreflexividad, asimetría y transitividad, lo cual se expresa en símbolos como sigue
Es de hacer notar que de comprobarse que una relación es de orden estricto también puede ocurrir que verifique las definiciones de orden parcial o la de orden total.

Al definir una relación de orden R⊂A2, para el caso de pares ordenados que pertenecen a la relación o elementos del conjunto A que están relacionados por medio de la misma, es común indicar que el primer elemento precede al segundo. Tal afirmación se denota a≺b y el símbolo ≺ se conoce como el signo preceder. En este sentido, las propiedades vinculadas a las definiciones de relación de orden se expresarían como sigue
En el caso de una relación de orden amplio
Y en cuanto a la relación de orden estricto
Por otro lado, en cuanto a la propiedad de linealidad queda expresada como sigue
Vale destacar que la expresión

se lee a no precede a b.

En un conjunto ordenado A por medio de la relación ≺ es posible determinar los siguientes elementos distinguidos
En relación a estos elementos es importante destacar algunas precisiones importantes:
No necesariamente un conjunto ordenado posea primer o último elemento, puede pasar que tenga alguno o ninguno, en caso de tenerlos son únicos.
En cuanto a los elementos minimales y maximales, en el caso de que existan no necesariamente son únicos.
En el caso de las cotas inferiores o superiores, si existen puede que no sean únicas, no obstante el ínfimo y supremo puede que no existan aunque el conjunto en cuestión sea acotado.

Sea ≺ una relación de orden definida en un conjunto A, se dice que el referido conjunto está bien ordenado si y sólo sí se demuestra que en el mismo la relación es de orden total (es decir, que existen pares de elementos comparables por medio de la relación) y además todo X⊂A diferente del vacío posee primer elemento.
Se puede citar como ejemplo el conjunto de los números naturales N definiendo en él la relación de orden menor o igual, en este caso se evidencia que el orden es total y además todo subconjunto de N posee primer elemento, inclusive el mismo N cuyo primer elemento es el cero. Tal situación no ocurre en otros conjuntos numéricos definiendo la misma relación de orden.

Como se ha indicado en el preámbulo, las relaciones de orden tienen una gran aplicabilidad en la vida diaria de los seres humanos, en tanto que éstos las promueven de manera frecuente en todo su quehacer para categorizar todos los procesos en los cuales se ve involucrado. Específicamente hablando, tenemos por ejemplo la relación menor que la cual es ampliamente utilizada para ordenar todo tipo de medida: estatura, distancia, temperatura, edad, estatura, talla, entre otras.
Asimismo, esta misma relación es utilizada en el ámbito social y estadístico para determinar los diferentes estratos sociales y económicos por la cantidad de recursos que se disponen, así como la brecha salarial entre naciones y otras variables macroeconómicas. En este mismo orden de ideas, el valor de las diferentes monedas puede ser ordenado como de hecho ocurre, por su poder adquisitivo en comparación con otras.
En cuanto al ámbito de la salud, son de gran importancia para comprobar la presencia o no de enfermedades dependiendo de menores o mayores valores de un determinado indicador dentro de un margen de confianza.
Si evaluamos los conceptos presentados y los contrastamos con nuestra realidad nos daremos cuenta de que forma interactuamos con las relaciones de orden en la mayoría de los casos de forma natural e imperceptible, como toda noción de la matemática es cuestión de mirar más allá de lo evidente.
En la próxima publicación se estarán presentando como de costumbre, precisiones de naturaleza práctica con el propósito de seguir afianzando los aspectos estudiados en torno a las Relaciones Binarias, nos leemos en el siguiente post, saludos y éxitos para todos los lectores y académicos de esta comunidad.

“No hay rama de la matemática, por lo abstracta que sea , que no pueda aplicarse algún día a los fenómenos del mundo real” - Lobachevski.

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia diseñadas en el editor de presentaciones Microsoft Powerpoint 2013, ajustadas y recortadas en Paint.
Publicaciones Relacionadas



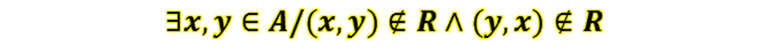
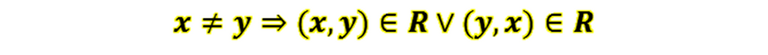
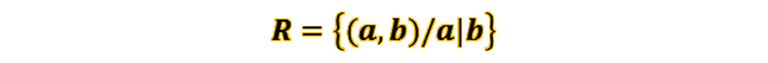
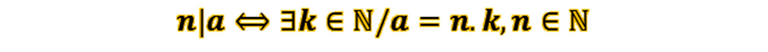

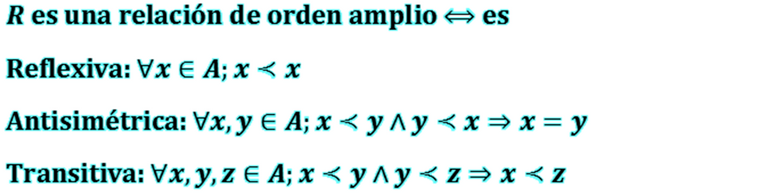

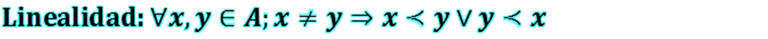

¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Entra aquí para más información sobre nuestro trail.Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Excelente y muy didáctico post @reinaseq, disfruté su lectura. Excelente tema. Mis cordiales saludos.
Muchas gracias @tsoldovieri, valoro que se tome la molestia de revisar la información que comparto y que tenga buenos comentarios del mismo!! Saludos fraternos!!
Buen post
Quiero sugerirte que uses la etiqueta HTML
para las expresiones y declaraciones matemáticas que haces. Podría hacer que luzcan un poco mejor a la vista del lector. Saludos., @ReinaSeq. Para aportar un ejemplo aplicativo de lo que planteas, esta "relación de orden" se hace evidente en el enfoque de Programación Orientadas a Objetos, donde hay que generar clases de objetos considerando su jerarquía, la agregación, composición, etc.Hola @eniolw, que buen ejemplo el que presentas, me alegra que evidencies la vinculación de los saberes que comparto con tu área de experticia, es muy motivador!! En cuanto a la sugerencia debo documentarme sobre la forma de utilizar el comando que me indicas, espero que se mantenga la fidelidad de las expresiones matemáticas al usarlo, gracias por los aportes!! Saludos cordiales!!
La etiqueta que te digo puedes usar es code.
@resteemator is a new bot casting votes for its followers. Follow @resteemator and vote this comment to increase your chance to be voted in the future!
Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!