Saludos a todos los lectores de la comunidad de Steemit que vienen haciendo seguimiento a mis publicaciones sobre Teoría de Conjuntos, en esta oportunidad es propicio presentar la demostración de algunos teoremas y propiedades a partir de la fundamentación teórica estudiada en mis post anteriores, los cuales se especifican a continuación (haciendo clic en cada título pueden acceder a la respectiva información):
Para tener una comprensión más clara es importante hacer revisión previa de los vínculos anteriores. Adicionalmente, es importante señalar que los planteamientos que se presentan a continuación son de la perspectiva algebraica, es decir, entendiendo que el Álgebra es una subárea de la Matemática que estudia y se enfoca en las generalidades de la misma, en este sentido se vale se letras que representan la generalidad del número con el propósito de comprobar que una determinada propiedad o teorema se cumple para todos los elementos de un conjunto o ámbito de la Matemática, y es, a partir de la referida comprobación que pueden utilizarse en situaciones particulares y concretas (ámbito numérico) con la certeza de que han derivado de un proceso de demostración satisfactorio. Generalmente se apoya de igual forma en las leyes de la Lógica Proposicional e Inferencial.
Es importante señalar, sobre todo a la población estudiantil que se forma en estos temas, que una demostración matemática no es un proceso forzado sino más bien sustentado en definiciones, leyes y axiomas, así como otras propiedades y teoremas que ya han sido demostrados, esto quiere decir, que el desarrollo de una comprobación fluye en la misma medida que existe un sustento teórico que le permite avanzar. Hay métodos de demostración directos (como los que se han venido presentando en publicaciones pasadas) e indirectos (como el contraejemplo, reducción al absurdo). A continuación comencemos con la selección de propiedades o teoremas a verificar:
Como podemos observar, el teorema presentado es una igualdad de conjuntos, esto indica que debemos aplicar la definición de Igualdad de Conjuntos y demostrar la doble inclusión. Procedamos:
i ¿[(A∪B)-C]⊂[(A-C)∪(B-C)]?
∀x∈[(A∪B)-C]⇒x∈(A∪B)∧x∉C, por definición de diferencia de conjuntos
⇒(x∈A ∨ x∈B)∧x∉C, por definición de unión de conjuntos
⇒(x∈A ∧x∉C)∨(x∈B∧x∉C), por ley lógica distributiva de la conjunción respecto de la disyunción inclusiva
⇒x∈(A -C)∨x∈(B-C), por definición de diferencia de conjuntos
⇒x∈[(A-C)∪(B-C)], por definición de unión de conjuntos
∴Se demuestra que [(A∪B)-C]⊂[(A-C)∪(B-C)], por definición de Inclusión de Conjuntos.
ii ¿[(A-C)∪(B-C)]⊂[(A∪B)-C]?
∀x∈[(A-C)∪(B-C)]⇒x∈(A -C)∨x∈(B-C), por definición de unión de conjuntos
⇒(x∈A ∧x∉C)∨(x∈B∧x∉C), por definición de diferencia de conjuntos
⇒(x∈A ∨ x∈B)∧x∉C, por ley lógica distributiva de la conjunción respecto de la disyunción inclusiva
⇒x∈(A∪B)∧x∉C, por definición de unión de conjuntos
⇒x∈[(A∪B)-C], por definición de diferencia de conjuntos
∴Se demuestra que [(A-C)∪(B-C)]⊂[(A∪B)-C], por definición de Inclusión de Conjuntos.
∴ Por i y ii se demuestra que (A∪B)-C=(A-C)∪(B-C), por definición de Igualdad de Conjuntos ∎
Al igual que el planteamiento anterior estamos en presencia de una igualdad de conjuntos, por lo cual nuevamente aplicaremos la definición de Igualdad de Conjuntos demostrando la doble inclusión. Llevemos a cabo el proceso de comprobación:
i ¿[(A-B)×C]⊂[(A×C)-(B×C)]?
∀(x,y)∈[(A-B)×C]⇒x∈(A-B)∧y∈C, por definición de producto cartesiano
⇒(x∈A ∧ x∉B)∧y∈C, por definición de diferencia de conjuntos
⇒x∈A ∧ (x∉B∧y∈C), por ley lógica asociativa de la conjunción
⇒x∈A ∧ (y∈C∧x∉B), por ley lógica conmutativa de la conjunción
⇒(x∈A ∧ y∈C)∧x∉B, por ley lógica asociativa de la conjunción
Ahora estamos en un punto en el cual se estaría requiriendo tener agregado con una disyunción inclusiva una expresión y∉C de manera que se pudiera aplicar una definición de producto cartesiano (cuando un elemento no pertenece a la misma) y obtener la segunda parte de la expresión a la cual queremos llegar, en este sentido, pareciera que no es posible justificar tal acción, no obstante, debemos recordar que para que una disyunción inclusiva sea verdadera basta con que al menos una de las proposiciones enlazadas con este conectivo lógico sea verdadera (de acuerdo a lo establecido en su Tabla de Certidumbre Fundamental), esto indica que por este motivo es posible adicionar lo que necesitamos sin importar su valor veritativo, en tanto que la disyunción inclusiva por su condición de veracidad lo permite. Asimismo, basado en estos principio teóricos existe la ley lógica de adición que respalda el procedimiento, esto es p≡p∨q, luego tenemos que
⇒(x∈A ∧ y∈C)∧(x∉B∨y∉C ), por ley lógica de adición y ley lógica asociativa de la conjunción
⇒(x,y)∈(A×C)∧(x,y)∉(B×C), por definición de producto cartesiano
⇒(x,y)∈[(A×C)-(B×C)], por definición de diferencia de conjuntos
∴Se demuestra que [(A-B)×C]⊂[(A×C)-(B×C)], por definición de Inclusión de Conjuntos.
ii ¿[(A×C)-(B×C)]⊂[(A-B)×C]?
∀(x,y)∈[(A×C)-(B×C)]⇒(x,y)∈(A ×C)∧(x,y)∉(B-C), por definición de diferencia de conjuntos
⇒(x∈A ∧ y∈C)∧(x∉B∨y∉C ), por definición de producto cartesiano
⇒[(x∈A ∧ y∈C)∧x∉B]∨[(x∈A ∧ y∈C)∧y∉C] ), por ley lógica distributiva de la conjunción respecto de la disyunción inclusiva
⇒[x∈A ∧ (y∈C∧x∉B)]∨[x∈A ∧ (y∈C∧y∉C)] ), por ley lógica asociativa de la conjunción
⇒[(x∈A ∧x∉B)∧ y∈C]∨[x∈A ∧ (y∈C∧y∈C')] ), por leyes lógicas asociativa y conmutativa de la conjunción y por definición de complemento de un conjunto
⇒[x∈(A-B)∧ y∈C]∨[x∈A ∧ y∈(C∩C')] ), por definición de diferencia de conjuntos y definición de intersección de conjuntos
⇒[x∈(A-B)∧ y∈C]∨(x∈A ∧ y∈∅), por propiedad de la intersección de conjuntos A∩A'=∅
⇒(x,y)∈[(A-B)×C]∨(x,y)∈(A×∅), por definición de producto cartesiano
⇒(x,y)∈[(A-B)×C]∨(x,y)∈∅, por propiedad de producto cartesiano se cumple la existencia del elemento neutro como sigue: ∀A⊂U, A×∅=∅×A=∅
⇒(x,y)∈{[(A-B)×C]∪∅}, por definición de unión de conjuntos
⇒(x,y)∈[(A-B)×C], por propiedad de unión de conjuntos ∀A⊂U, A∪∅=∅∪A=∅
∴Se demuestra que [(A×C)-(B×C)]⊂[(A-B)×C], por definición de Inclusión de Conjuntos.
∴ Por i y ii se demuestra que (A-B)×C=(A×C)-(B×C), por definición de Igualdad de Conjuntos ∎
La demostración que se acaba de realizar resulta muy interesante, en tanto que no es similar a anteriores comprobaciones que se han presentado en publicaciones anteriores en las cuales se visualiza que la segunda inclusión se resuelve devolviéndose por los pasos de la primera inclusión, en esta nos damos cuenta que tal situación no es posible y tuvimos que valernos de definiciones, leyes y propiedades en su mayoría diferentes en cada una de las comprobaciones i y ii. Lo ocurrido es muestra de la importancia de tener un buen dominio teórico para poder afrontar con éxito estas eventualidades, que para muchos representan retos que valen la pena afrontar. Continuemos con la siguiente demostración:
Esta expresión es diferente a las presentadas anteriormente, en tanto que el conectivo principal de la misma es un bicondicional. Estas situaciones nos recuerdan el siguiente polinomio lógico
La referida equivalencia nos muestra que comprobar un conectivo bicondicional pasa por demostrar p→q al cual se le llama Teorema Directo y q→p al cual se le conoce como Teorema Recíproco. Procedamos a la demostración:
i Teorema Directo: ¿A⊂B∧A⊂C⇒A⊂(B∩C)?
La forma lógica p→q nos indica que p es la hipótesis y apoya la demostración cuando se requiera y q es la tesis, es decir, lo que se quiere comprobar. En este caso, nuestra tesis es una inclusión, por tanto debemos demostrar que los elementos del primer conjunto pertenecen al segundo conjunto de acuerdo a la definición. Procedamos entonces:
¿A⊂(B∩C)?
∀x∈A⇒x∈B∧x∈C , por hipótesis tenemos que A⊂B∧A⊂C
⇒x∈(B∩C) , por definición de intersección de conjuntos
∴Se demuestra que A⊂(B∩C), por definición de Inclusión de Conjuntos.
ii Teorema Recíproco: ¿A⊂(B∩C)⇒A⊂B∧A⊂C?
En este planteamiento aplicamos el mismo razonamiento lógico referente a la hipótesis y la tesis, salvo que en este caso tenemos dos demostraciones en la tesis, a saber, dos inclusiones vinculadas con un conectivo conjunción, esto indica que si alguna de las dos inclusiones no es cierta entonces no se verificaría el teorema recíproco. Ahora vayamos al proceso demostrativo:
¿A⊂B?
∀x∈A⇒x∈(B∩C) , por hipótesis tenemos que A⊂(B∩C)
⇒x∈B∧x∈C , por definición de intersección de conjuntos
⇒x∈B, por ley lógica de simplificación p∧q≡p (o también p∧q≡q)
∴Se demuestra que A⊂B, por definición de Inclusión de Conjuntos.
¿A⊂C?
∀x∈A⇒x∈(B∩C) , por hipótesis tenemos que A⊂(B∩C)
⇒x∈B∧x∈C , por definición de intersección de conjuntos
⇒x∈C, por ley lógica de simplificación p∧q≡p (o también p∧q≡q)
∴Se demuestra que A⊂B, por definición de Inclusión de Conjuntos.
∴Por las demostraciones de los teoremas directo y recíproco se cumple que A⊂B∧A⊂C⟺A⊂(B∩C)
Demostraciones Propuestas
Con el propósito de ejercitar y/o apoyar el proceso formativo de los participantes de la comunidad de Steemit que estén cursando cursos donde estos saberes son pertinentes se dejan propuestas las siguientes demostraciones:
Como siempre, es un placer compartir saberes matemáticos con la audiencia, nos leemos en la próxima publicación.

La matemática es llave y puerta de la ciencia - Roger Bacon .

Referencia
Armando, R. (2001). Algebra I. Edición XX. Editorial El Ateneo.
Lipschutz, S. (1970). Teoría de Conjuntos y Temas Afines. Teoría y 530 problemas resueltos. Serie de compendios SCHAUM. Mc Graw-Hill.
Todas las imágenes, separadores y banners de este artículo son de autoría propia.
Artículo Anterior





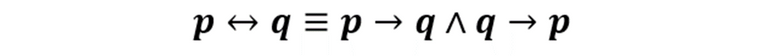
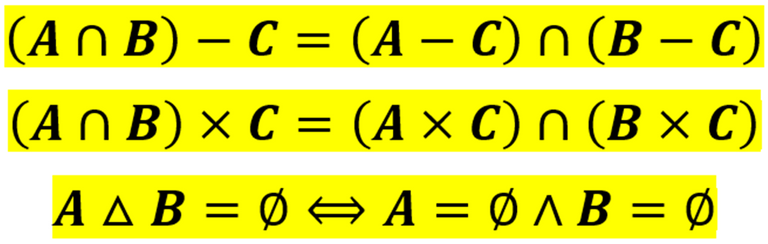
Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.Congratulations! This post has been upvoted from the communal account, @minnowsupport, by reinaseq from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Muy agradecida por el apoyo recibido, saludos cordiales y bendiciones!!!
Canal Discord ¡Te esperamos!Votado por el trail @team-mexico
Delegaciones para @team-mexico ¡Ayúdanos a crecer!
10 SP - 25 SP - 50 SP - 100 SP - 150 SP- Mas información.
.png)
Agradecida con @team-mexico, siempre atentos y diligentes a prestar su apoyo a la comunidad de Steemit!! Abrazos!!
Excelente, muchísimas gracias por valorar mi producción, son siempre bienvenidos!! Saludos cordiales!!