Hola amigos, hoy continuamos hablando sobre semiconductores. En esta ocasión se estará hablando sobre resistividad eléctrica.
Si no has visto la primera parte, la puedes ver aquí
Fuente de la imagen
La densidad de corriente debida a huecos (e) y electrones (-e) es igual al producto de su densidad de carga y velocidades respectivas. Por tanto, la densidad de corriente o la densidad de carga por unidad de tiempo transportada por huecos y electrones es:
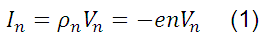
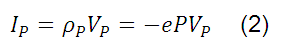
Donde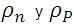 
se refieren a las densidades de carga asociadas con las densidades de electrones y huecos n y p. 
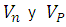son las velocidades vectoriales promedio de los electrones y huecos respectivamente.
Puesto que la velocidad electrónica promedio es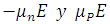 
para electrones y huecos, donde 
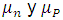son las movilidades del electrón y el hueco, y E el campo eléctrico; las ecuaciones (1) y (2) se pueden escribir de la siguiente manera:
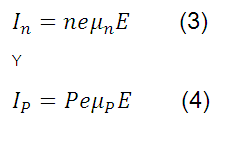
Entonces, la densidad total de corriente eléctrica I se puede expresar como:
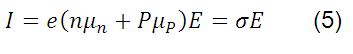
Donde la conductividad eléctrica σ está dada por:
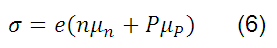
Entonces, la resistividad eléctrica (ρ) de un material viene dada por:
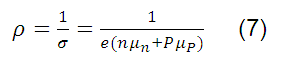
Donde las movilidades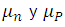 
se definen como:
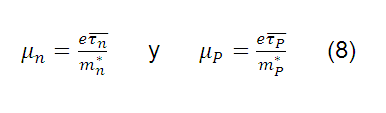
Donde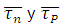 
son los promedios ponderados de los tiempos de relajación para electrones y huecos sobre la distribución Maxwell-Boltzmann. Los términos 
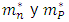representan la masa efectiva de los electrones y huecos respectivamente.
También se debe observar que n y p son los valores instantáneos reales de la concentración de huecos y electrones que no necesariamente son idénticos a las densidades de equilibrios de huecos y electrones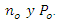 
Hasta ahora se ha supuesto que no existen gradientes de densidad de portadores que están relacionadas con el estado de equilibrio, de allí se deduce lo siguiente:
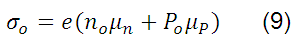
Donde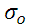 
es el valor correspondiente de la conductividad eléctrica.
Es necesario establecer esta distinción, porque es posible crear densidades de portadores en exceso de los valores de equilibrio en los semiconductores.
Para un semiconductor intrínseco con densidades de portadores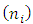 
iguales a los valore de equilibrio, 
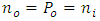, la ecuación (9) toma la siguiente forma:
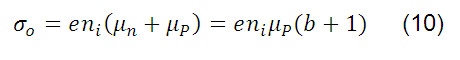
Donde b se define como la relación entre la movilidad de los electrones y los huecos, es decir:
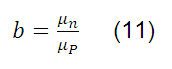
Para dicho semiconductor, su resistividad es la siguiente:
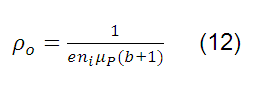
Si definimos 
, que representa el número de huecos o electrones por unidad de volumen dentro de una muestra intrínseca del semiconductor en función de la temperatura (T), por medio de la siguiente relación:
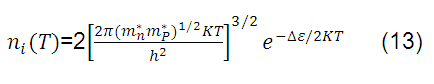
donde ∆ε es la brecha de energía prohibida del semiconductor, es decir, es la diferencia de energías entre la banda de conducción y la banda de valencia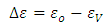 
El termino K es la constante de Boltzmann y h representa la constante de Plank.
Usando la ecuación (10), podemos escribir la ecuación (13) de la siguiente forma:
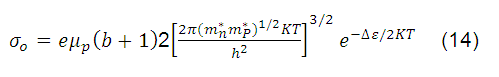
Puesto que la movilidad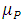 
tiene casi siempre una dependencia de la temperatura que anula en su mayor parte la variación de la temperatura 
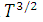del término que precede el factor exponencial y, puesto que b no depende mayormente de la temperatura, la variación anterior de 
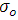como una función de 1/T es esencialmente exponencial.
Por otro lado, para un semiconductor que no es necesariamente intrínseco, es decir, extrínseco, la conductividad está dada por la ecuación (9).
Si usamos la ecuación (11) para eliminar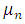 
, se obtiene la siguiente ecuación:
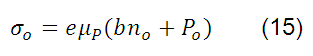
Luego, usamos las siguientes ecuaciones para sustituir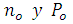 
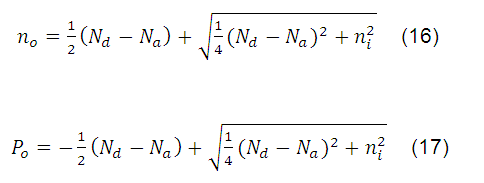
Donde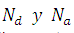 
son las concentraciones de donadores y aceptores respectivamente.
La conductividad se puede escribir como:
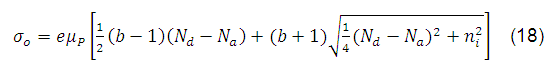
Finalmente, la resistividad del semiconductor extrínseco es:
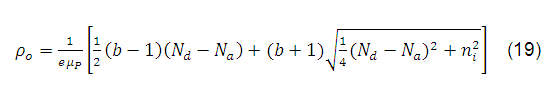
REFERENCIAS
Kittel, C. Introduction to solid state physics, John Willey & sons, INC. New York. 1954.
Mckelvey, J. Física del estado sólido y de semiconductores. Editorial Limusa. México D.C. 1976.
S.M. Sze. Physics of semiconductor devices, Weley-Interscience, second edition. 1981.
Hall, H. E. Física del estado sólido, editorial Limusa. México D.C. 1978.
Todas las ecuaciones aquí mostradas fueron escritas usando Microsoft Word 2010.
Saludos estimado @taborda-charrouf
Son bienvenidas tus contribuciones en la comunidad #stem-espanol.
Aquí puedes compartir tus conocimientos, análisis y discusión de este tema que me apasiona en lo particular, ya que tengo unos años trabajando en la caracterización eléctrica de materiales semiconductores y se que tu aporte será un beneficio para esta comunidad científica!
Hola @iamphysical. ¡gracias!
espero seguir compartiendo artículos de este estilo y poder aprender de los publicaciones de otros compañeros.
¡Saludos!