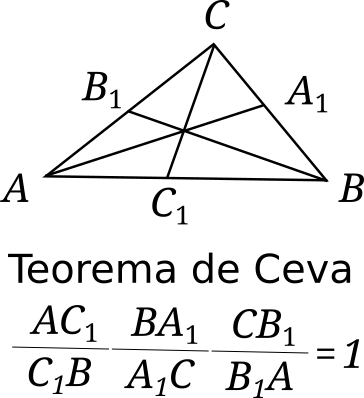
Las rápidas muestras de inclinación y genio del mozalbete hacia la disciplina conducen a los hermanos Ceva (Tomaso y Giovanni) a orientarlo por este camino. Ambos hermanos han ganado en el momento un sólido prestigio, y al tocayo de nuestro personaje lo conocemos hoy por un teorema, que establece una bella relación aritmética entre las rectas que concurren a ternas en el interior de un triángulo. Saccheri recibe de estos maestros los volúmenes de los Elementos de Euclides traducidos por el propio Clavius y pronto da cuenta de su lectura, con la publicación de su primer libro Quaesita geometrica, una colección de problemas de geometría en la que, aun cuando no expone su posterior creatividad, deja ver una penetración inusual en el tema.
Al año siguiente de esta publicación, en 1694, se ordena sacerdote y sus dotes pedagógicas le llevan a la enseñanza filosófica y a la lógica, caminando entre los rigurosos vericuetos euclidianos. Tres años necesita para producir una obra hoy reconocida como magistral: Logica demonstrativa en la que hace análisis y clasificación de las definiciones en general. Esta obra estuvo perdida durante muchos años, de hecho hasta 1903 cuando Giovanni Vailati la redescubre y exige para ella lugar preminente en la historia de la lógica.
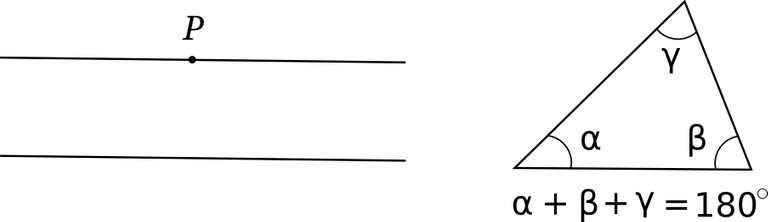
Pero su creación máxima estaba por venir y Logica demonstrativa apenas le servía de pórtico. El título de por sí es extraño: Euclides ab omni naevo vindicatus (Euclides liberado de todo error): denota profunda preocupación por el prestigio del maestro. Ocupa sus páginas un detalle de la gigantesca obra euclidiana, en la que ya había reparado la tradición: el quinto postulado... largo enunciado, carente de la "evidencia" y simplicidad de sus cuatro y únicos compañeros anteriores. Hasta el poeta Omar Khayyam le había dedicado sus Discusiones sobre las dificultades en Euclides, adelantando algo de la visión del italiano, pero no parece que éste haya tenido contacto con la obra del persa. En todo caso, el postulado contenía una rotunda afirmación sobre las rectas paralelas: por un punto que está fuera de una recta dada es dable trazar una paralela a ella, pero no podemos esperar más que esa paralela, no cabe otra por ese punto. (No redactó el griego su postulado de esta manera, pero estamos hablando de la esencia, no de la forma.) El quinto postulado obliga a que sucedan cosas muy interesantes, como que los ángulos intermos de todo triángulo suman 180 grados o el teorema de Pitágoras. Es más, esas afirmaciones son el quinto postulado expresado en otras palabras.
Lo cierto es que el dichoso quinto postulado era una piedra en el zapato (o la sandalia, si se quiere) para todo el que se ocupara en serio de la obra euclidiana. Su diferencia formal con los otros cuatro postulados lo hacían sospechoso de merecer ese nombre. Hay quienes dicen que la sospecha embargaba hasta al propio Euclides, y tratan de clasificar a éste como el primer geómetra no euclidiano, atribución algo excesiva a mi parecer. Pero si no es un postulado, es decir algo que ha de aceptarse sin demostración, entonces por fuerza es una proposición o teorema, es decir, algo que ha de demostrarse usando los otros postulados. Muchos lo intentaron, antes y después de nuestro Saccheri, y cantaron un ¡Eureka! que se disolvía apenas se comprobaba que en sus pretendidas demostraciones hacían uso del mismo postulado, pero escrito de otra manera.
El jesuita genovés emprende la tarea, al igual que sus predecesores, armado con una formidable herramienta griega: la reducción al absurdo, particular forma lógica de adquirir la verdad por el procedimiento de negarla, para que tal atrevimiento nos meta en aprietos al hacer aparecer la contradicción, esa mancha negra e indeseada del pensamiento matemático. Aun más: se trata de una doble reducción al absurdo. ¿Por qué? En toda situación de equilibrio, hay un centro y dos extremos. Al centro justo, los griegos le llaman parabolé, uno de los extremos es deficiente o eleipsis y otro es excesivo o hiperbolé. La geometría euclidiana es el centro justo para Saccheri, por lo cual al negar el quinto postulado se obliga a asumir por separado cada uno de los extremos y demostrar que ambos conducen a contradicción. La única opción entonces sería regresar al centro justo.
Para situarse en el extremo excesivo o hiperbolé, Saccheri adopta una suposición a la que llama hipótesis del ángulo obtuso; desplazado al extremo deficiente o eleipsis, bautiza a la nueva suposición como hipótesis del ángulo agudo. Moviéndose en ambas corrientes navega el río de la lógica y demuestra proposición tras proposición, deducidas de las suposiciones violatorias. Y lo hace con fluidez: la contradicción no aparece. Al menos no lo hace en un sentido estrictamente lógico, cosa que un lógico de la talla de Saccheri no debía haber pasado por alto: el genovés estaba haciendo nuevas geometrías.
Y he aquí el verdadero problema de nuestro pensador: la tradición, en su forma más nociva -el prejuicio-, se le imponía. Los siglos le daban al pensamiento euclidiano el rango de interpretación del universo, de manera que pensar en geometrías diferentes a las del alejandrino era casi como un atentado contra Natura. El prejuicio, cual Titán amenazado, le exige a Saturno que destruya su descendencia y éste obedece devorando a sus propios hijos: en la proposición 14 de su opus magnum Saccheri da cuenta del primero: La hipótesis del ángulo obtuso es absolutamente falsa, puesto que se destruye a sí misma, mientras que en la 33, engulle al segundo: La hipótesis del ángulo agudo es absolutamente falsa, puesto que repugna a la naturaleza de la línea recta.
Confiaba así el sacerdote jesuita, con estos dos dictámenes, haber librado al sabio alejandrino de la duda que la Historia le impuso. La misma Historia que sepultó su propia obra en el olvido, hasta el feliz día de 1883 en que Eugenio Beltrami redescubre su fallida vindicación. ¿Podríamos acusarlo de timorato o servil? Sería desconocer el peso de algunos imponderables. Bastaría observar la conducta del mismísimo Carl Gauss -el gigante Carl Gauss- quien, en poder de esta materia por genio propio, decidió mantenerla dentro de sus cuadernos por temor a "la gritería de los beocios", echando mano de Plutarco para aludir a los discípulos de Kant, defensores del apriorismo de las ideas de forma y espacio que, según ellos, se recogía en la geometría de Euclides. No obstante, también el ego es una fuerza muy poderosa y cuando Farkas Bolyai comentó, a su amigo Gauss, los descubrimientos de su hijo János en esta materia, el alemán se apresuró a aclararle que "felicitar a tu hijo es como felicitarme a mí mismo" y dio a sus anotaciones la luz previamente negada.

Excelente post @dougjim, pero veo que no es reconocido como tal; por ello te invito a usar nuestra etiqueta proconocimiento. Lee sobre nosotros en @proconocimiento, equipo que arbitra y valora contenido como el que tú nos presentas en tu post.... Una recomendación, coloca las fuentes de las imágenes y asegurate de que no estén sujetas a derecho de autor.
Gracias. Usaré la etiqueta para el próximo post. En este caso, excepto las fotos finales, todas las imágenes son mías.