The voting algorithm applies used_power both to the value rewarded and the draw-down from current_power.
Thus the total value which can be rewarded from any level of voting power is always the same for an equal sized section of the voting power drawn-down.
If we set a₁ to the value of a 100% vote and r to the factor that the voting power decreases for each 100% vote, then the total value of the maximum possible votes in rapid succession before any regeneration of voting power is an infinite geometric series:
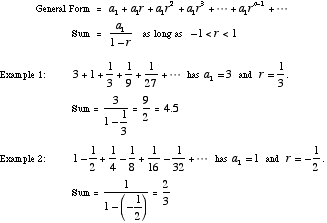
Thus if a₁is 100% of its value and r is 0.98, then total value of maximum possible votes is 50 times its value for a 100% vote. And if a₁is 80% of its value then total value of maximum possible votes is 40 times its value for a 100% vote. And ditto for a₁at 60%, 40%, 20% of its value then total value of maximum possible votes is 30, 20, 10 times its value for a 100% vote respectively. Thus we can see any sectioning of the voting power provides equal total value. This is because more votes can be made at the lower voting power levels because the voting power decreases slower.