😵
Use unicode. The above weird face is unicode 128565 and I added it by typing 😵 ; but here I added a space between the unicode and the semicolon so that you could see the format.
A super easy way to do this is to go here:
http://math.typeit.org/
And then enter the math and copy/paste it right into steemit.
∀∃⇒ηΦ¼∈√765→η∈ℂ
∑α
Compare:
∀(x, y ∈ A ∪ B; x ≠y) x² − y² ≥ 0
For all (x, y :- A u B; x != y) x^2 - y^2 >= 0
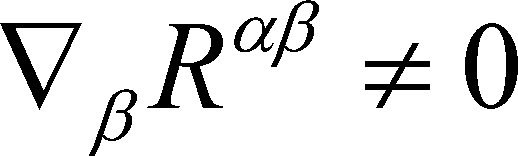
Steemit.chat has support for TeX equations using KaTex. Something like that or MathJax would have been terrific for Steemit, too.
I wanted to type the differentiation symbol and googled for it. Nice tool that will come handy. Bookmarking it now.
Check out my Math is Fun Series
Thanks! Now I can write math formulas in my posts! Planning on writing articles about Gödels incompleteness theorem and algorithmic information theory.
hey man Thanks for upvoting my friends @uncerntropy and his new post about Bitcoin and financial freedom, and yeah man Math is amazing look at how Math has changed the world with crypto currency and how simpole math algorithms have generated hundreds of billions of dollars out of the Aether but are now more real than dollars and more valuable than Gold
Wow Godel? incompleteness theorem?
https://en.wikipedia.org/wiki/G%C3%B6del%27s_incompleteness_theorems
"Gödel's incompleteness theorems
From Wikipedia, the free encyclopedia
Gödel's incompleteness theorems are two theorems of mathematical logic that demonstrate the inherent limitations of every formal axiomatic system containing basic arithmetic.[1] These results, published by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of mathematics. The theorems are widely, but not universally, interpreted as showing that Hilbert's program to find a complete and consistent set of axioms for all mathematics is impossible.
The first incompleteness theorem states that no consistent system of axioms whose theorems can be listed by an effective procedure (i.e., an algorithm) is capable of proving all truths about the arithmetic of the natural numbers. For any such formal system, there will always be statements about the natural numbers that are true, but that are unprovable within the system. The second incompleteness theorem, an extension of the first, shows that the system cannot demonstrate its own consistency.
Employing a diagonal argument, Gödel's incompleteness theorems were the first of several closely related theorems on the limitations of formal systems. They were followed by Tarski's undefinability theorem on the formal undefinability of truth, Church's proof that Hilbert's Entscheidungsproblem is unsolvable, and Turing's theorem that there is no algorithm to solve the halting problem."
hey and i upvoted all your recent comments! heres the screenshot proof!
Thanks for helping my new steemit user friend @uncerntropy he will keep posting good articles like that!
hey I followed you! I need to support more Math Enthusiasts with my steempower!
Good idea.
PS The x ≠y condition is unnecessary :^)
PPS There's a "howto" tag.
PPPS Ricci tensor, yay!
Wow! Someone who knows the Ricci tensor on Steemit! Do you study QED as your name suggests? Followed!
www.AxiomsOfChoice.org
COOL! I'm totally going after the howto tag. These equations are meaningless other than just demonstrating the method.
But now you have another tag open :)
Maybe...science?
x̂ is a unit vector in the x direction
ŷ is a unit vector in the y direction
x̂ŷ  =  i  =  √-̅1̅
Z Â = Â x + iy
x̂Z  =  x̂x + x̂iy  =  x̂x + x̂x̂ŷy  =  x̂x + ŷy
Cool, Thanks for the useful tip.
😵
Nice content, come on join a
Thanks - upvoted and resteemed. I'd like to include a link to this article in the next Math-Trail Magazine - hope that's OK with you!
!-=o0o=-!
To follow curated math content follow @math-trail.
If you wish @math-trail to follow you then read this article.
Click here for Mathematics forum on chainBB
Thanks for the tip.
This is pretty awesome, I've seen some math posts that doesn't look so good because of the lack of math symbols.
Wow this is awesome! Thanks for the advice! Only wish I caught it in time to upvote.
But I don't see how to write fractions. The slash like 2∕3 isn't the correct notation for a fraction. You cannot write the midnight formula to solve the quadratic equation with a slash!