Introduction
I would like to start this article from famous quote by brilliant mathematician.
The shortest path between two truths in real domain passes through complex domain.
Jacques Hadamard
Imaginary numbers are often suitable to use to solve the real problems. The extension of numbers from Natural to Complex number has always made real application wide and easy. The syllabus of high school mathematics for complex number is good for basic stuffs but for competitive exams and Olympiad,its necessary to have further knowledge on complex number. To introduce about applications of complex number beyond syllabus this article is written.
This article doesn't include full description of all applications yet it gives you enough introductory ideas and motivations to learn more and it endeavors to show you the magic of complex numbers.
Complex number in Exponential form:
Functions have different representations. They can be represented by infinite sum containing derivatives of function at a point x=a. It is called Taylor series. If the point is at x=0, then it is special case of Taylor series called Maclaurin series. With the help of Maclaurin series, we can prove Euler's Identity which is given below.

Proof:
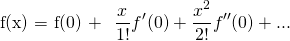
Here, f'(x) denotes derivative with respect to x.
If f(x) = cos x, f(0) = 1
f'(x) = sin x, f'(0) = 0
f''(x) = cos x, f''(0) = 1
f'''(x) =- sin x , f'''(0)= 0
so,
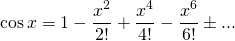

Similarly;

and,

or, 
or, 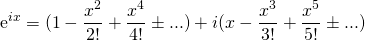
or,

Putting, x = θ
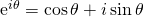
It is called Euler's Identity named after great mathematician Leonard
Euler.
This identity relates trigonometric functions and exponential function
with the help of complex number.
Let us put, x = π
then, the identity becomes:
 = cos π + i sin π
= cos π + i sin π
 = -1
= -1
 + 1 = 0
+ 1 = 0
(forget about application, Look! at this identity, it contains e,π,1,0 and i. Ponder, How beautifully they have placed themselves in this beautiful identity.)
- e is called Euler's number.
- It is irrational and Transcendental Number.
- It is defined as:
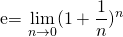
- π is defined as ratio of circumference of circle to the diameter of same
circle. - It is irrational and Transcendental Number.
(Transcendental numbers are those numbers which cannot be the solution
of algebraic equations. 2 is irrational but it isn't transcendental number.)

which is the expression of complex number in exponential form.

Solving,
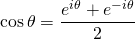

i) If f(x + y) = f(x) + f(y)
f(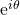 ) = f(cos θ ) + if (sin θ)
) = f(cos θ ) + if (sin θ)
If f(x) is function and f'(x) be its derivative w.r.t. x
= i(cosθ + i sinθ)
= - sin θ + i cos θ
comparing real and imaginary parts:f'(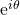 ) = f'(cos θ) + i f'(sin θ)
= i
) = f'(cos θ) + i f'(sin θ)
= i 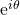
or, f'(cos θ) = - sin θ
or, f(sin θ) = cosθ
Exercise:
There is some transform(actually its Laplace) such that L(x+y) = L(x) + L(y).
Given that, e^it = cos t + i sin t. If Laplace transform of e^it is  , Find the Laplace transform of cos t and sin t.
, Find the Laplace transform of cos t and sin t.
It makes integration easy to evaluate.
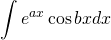
We know,
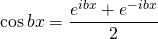
= 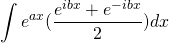
= 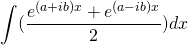
= 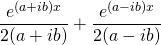
= 
= 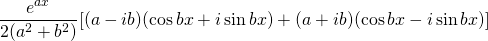
= 
Proving Trigonometric Identities:
Complex numbers can be used in exponential form to prove trigonometric identities.
Basic Trigonometric Identities:
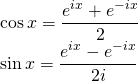
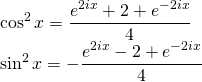
Adding we get,
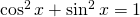
Exercise:
Prove that:
i) 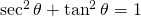
Expression for Multiple angles
Consider,

Comparing real and imaginary parts;

Formula for compound angles:
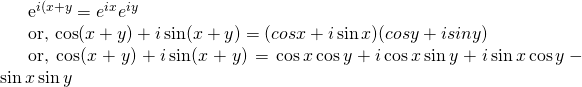
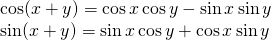
Exercise:
i. Find cos 5θ and sin 5θ in terms of sinθ and cosθ using de-Moivre
Theorem.
ii. Prove that: sin(x +y) = sin x cos y + cos x sin y
Relation Between Hyperbolic and Trigonometric functions:
Hyperbolic and trigonometric functions can be expressed in terms of exponential. So, they can be related with the help of complex number.
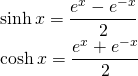
put x = i x

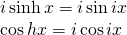
It enables us to use complex arguments:
consider:
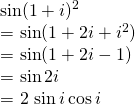

Also,
sin(x + iy) = sin x cos iy + cosx sin iy
= sin x cos hy + i cos x sin hy
Exercise:
i) sin(1 + i)^3
ii) sin(2 + 3i)
Logarithm of Negative Numbers:
Square root of negative number has no real solution but when we extended it to complex number, we defined it to have value. Similarly, log(x) has no real solution for x < 0. But, it has solution in complex domain.
we know,

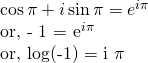
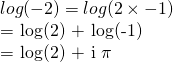
so in general:
If N is negative integer then,
log(N) = log|N| + iπ
Also,
-1 = e^iπ
taking square root on both sides,
i = e^{iπ/2}
Taking power i on both sides.
i^i = e^{- π/2}
It is real.
so, complex number powered to complex number may be real.
log (re^iπ)
= log r + iπ
for log (i + 1)

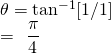
log(i +1) = 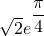
Exercise:
Write in terms of x + iy
i) log (i + 1)
ii)log (3i)
Solving Trigonometric Equations:
Since we entered the domain of complex number, many thing got extended. Here, I present one more. sin x = 2
Does it have real solution? Of course no since range of function f(x) = sin(x) in real domain is [-1,1] but in complex domain things are different. It has indeed solution.
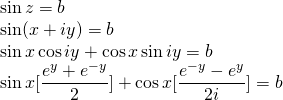
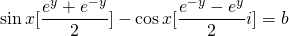
Comparing real and imaginary parts.

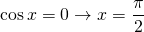
or,
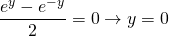
it implies, the complex number is purely real and holds for b in [-1,1].
But,
if x = π/2
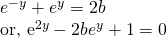
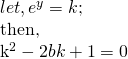
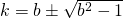
or, 
or, y = 
or, 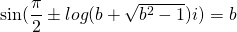
or, 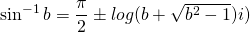
or, 
= 1.5708 + 1.31696 i
References:
i. Complex numbers from A to Z, Titu Andreescu
ii. Visual Complex Analysis, Needham
iii. Complex Functions: An Algebraic and Geometric Viewpoint. Gareth jones
Coded on:
i. www.quicklatex.com
Being A SteemStem Member
This post has received a 10.00 % upvote, thanks to: @bikkichhantyal.
2.01% @pushup from @bikkichhantyal
You got a 1.09% upvote from @postpromoter courtesy of @bikkichhantyal!
Want to promote your posts too? Check out the Steem Bot Tracker websitevote for @yabapmatt for witness! for more info. If you would like to support the development of @postpromoter and the bot tracker please
wowow
great post