Euler Identity: why is it beautiful?
Mathematics is a tool through which we understand nature. We may use the English language to communicate with each other. Likewise, the hidden workings of nature are expressed in terms of equations, numbers, identities, expressions etc. There are many of such kinds but some are particularly beautiful. The term beautiful can be subjective. In this article, I will try to explain why Euler’s identity is beautiful from my perspective.
.png)
The above photo is created by me in Adobe illustrator and it is a Euler identity. Identity in mathematics in simple term means equality. Like 1 + 1 is equal to 2. So, 1 + 1 = 2 is an identity. Well, this is reasonable and of course, numbers can be added. But, how can letters be added and multiplied?
I hope you already know about basic addition, subtraction, multiplication and division. So, let me start with power.
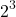 means to multiply 2 three times like
means to multiply 2 three times like  = 8 so,
= 8 so, 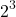 = 8
= 8
So, the above identity means multiplying e, iπ times when added to 1 results to nothing.
Now I would like to explain what these letters e, i and π represent.
The Euler Number(e)
The first constant in the identity 'e' is called the Euler number. It is by the name of great mathematician of 17th century, Leonard Euler. He was the one who named this constant. Though, it was named by him, it was actually discovered by Jacob Bernoulli (1655-1705) during the study of compound interest.
Consider a bank in which you get interest with 100% rate at the end of the year. If you invest 1 dollar in the bank, the amount you get at the end of the year is:
A =  = 2
= 2
If the bank pays the interest at the end of every six months. The interest you get from first six months will be added to the principle and in the next six months, the interest will be added from new principle. So, the amount of money at the end increases.
the amount of money you get at the end of the year is:
A =  = 2.25
= 2.25
If the bank pays interest making more intervals, the amount of money you get is increasing. Let's find out if the interest paid is monthly.
A =  = 2.613...
= 2.613...
If interest paid is daily;
A =  = 2.714567482 ...
= 2.714567482 ...
There is growth in the amount but with the increasing intervals, the amount growth is not proportional. Finally, let's check what if the interest is paid secondly;
A =  = 2.7182817813
= 2.7182817813
Now, the amount is approaching towards a finite value. In this case, we say that it is converging. The finite value towards which it is converging is Euler number(e). The value is 2.71828.... In calculus, it is defined in terms of limit as;
 = e
= e
Properties of Euler number:
i. It is an irrational number that means it cannot be expressed in the form of p/q where p and q are integers and q not equal to 0. That equivalently means, its decimal is non-terminating and non-repeating.
ii. It is a transcendental number that means it cannot be the solution of algebraic equations.
iii. Another interesting thing about an exponential function is, the differential of the function is the function itself.

iv. The exponential function can be expressed as Taylor series.

The magical imaginary unit (i)
In 1545, Cardano encountered with the complex number in his book Ars Magna while solving general cubic equation. Bombelli later introduced the procedure to solve an equation.
The imaginary unit is the square root of -1. If a^2 = b, then a is the square root of b. From the definition,i^2 = -1.
The square of the positive number is positive, i.e. 2^2 = 4, 5^2 = 25 etc.
The square of the negative numbers is positive, i.e. -1^2 = 1, -5^2 = 25 etc.
Then, how can the square of something be negative? Particularly -1 in this case?
At first, only counting numbers were in use. The counting numbers like 1,2,3 … are called natural numbers. Let’s do the subtraction of larger number from the smaller number.
1-3 =?
You may say its easy -2. But, when we didn’t have the proper notion of negative numbers, it was strange like above question. The result was not in the natural number system. We resolved this situation by extending number system to integer number system.
The division took number system to rational number system. Then came square root of 2. The decimal was non-repeating and non-terminating. So, number system extended to set of rational and irrational number formed. We called that real number system.
Let do the similar thing in above case. Then, the magical complex unity 'i' was introduced and defined as the square root of -1. This increased the scope of mathematics and opened the door for further manipulations. Analytical continuation, residue theorem, solving complex equation etc. may be some magic which I would cover in later posts. Let me give you simple mathematical magic.
“We can find cube root, 999th root, πth root even ith root. Whatever complex root we chose and whatever complex number we apply it to.”
(Roger Penrose)
The glorious Pi(π)
π pronounced as pi is the sixth letter of Greek alphabet which is the symbol for the ratio of circumference to the diameter of the circle.This ratio doesn’t depend upon the size of the circle. So, π is constant. The circumference of the circle is the linear distance around circle and the diameter of circle is the linear distance across circle passing through center of circle.
π is known to human for 4000 years. The ancient Egyptians and Babylonians had roughly estimated its value. The value of π was improved by Archimedes. He circumscribed and inscribed different polygon to improve value. Now with the help of computer, its value has been calculated up to trillion digits. Actually, we don’t need all digits. 39 digits are enough to calculate circumference of observable universe with in a hydrogen atom. It is used to check the computing power of super computers.
The value of π is 3.1415926535897… It is an irrational number. It is a transcendental number. Its value is calculated by following relation.

[PS: The above relation comes from Taylor series expansion of arc tan(x)]
Now, with the values;

Conclusion:
i. e, i, π, 1 and 0 are fundamental constants which are themselves beautiful. The implications of these in mathematics is profound. It is described by the history and importance of these numbers.
ii. These constants are from different fields of mathematics. Pi(π) is from the geometry. Iota(i) is from the complex number system. e is from the analysis(limit) and 1,0 are from number theory. These important numbers from different fields have arranged themselves in harmony in Euler Identity.
iii. The irrational number multiplied to irrational times imaginary numbers when added to 1 results in nothing. This is strange and strange is beautiful.
iv. At last but not the least, the existence of this identity is itself beautiful.
Citations: