Here are some examples of "Logistic Growth" models used to predict the population of different organisms over time.
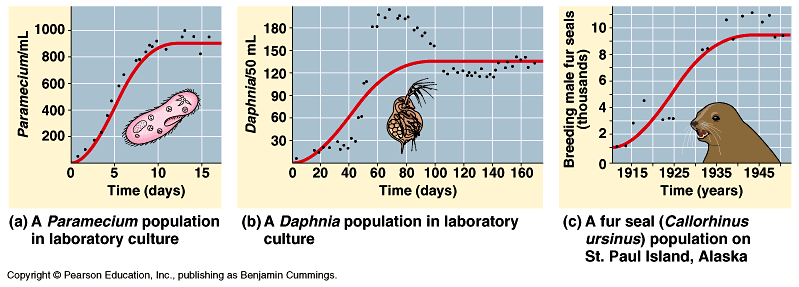
As you can see, according to this model, a population grows fast initially, but slows and approaches a certain "cap" called the carrying capacity.
We've seen in a previous post that a basic model for population growth is the rate of population increase is proportional to the current population, or...
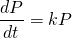
This differential equation describes exponential growth, where the growth rate dP/dt increases and the population P increases.
It might be a reasonable model if a species is given ideal growth conditions such as:
- Unlimited resources and space
- No predators
- Adequate nutrition
- Immunity from diseases
However, as we can clearly observe around us, no such conditions exist for any species, for if they did, it would be to the detriment of other species given the world's finite resources.
The exponential model of growth may be a good approximation initially, as displayed by bacterial cultures in a petri dish. However, the growth starts to slow and population levels off when it reaches a level that can no longer sustain an increasing growth rate.
We need a model that can approximate the declining rate of growth. What if we set up the differential equation as follows...
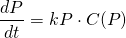
...where C(P) is a coefficient that depends on the population P, such that:
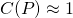
...in the initial stages, when the population is low.
And in the later stages,
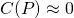
...when population growth can no longer be sustained.
This way, in the beginning, the model for population growth in the early stages is an approximation of the exponential model...
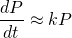
And at a time when growth can no longer be sustained, the growth rate is...
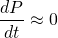
Such a coefficient may be described by
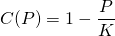
where K is called the carrying capacity for a given population - which is the maximum number that a species can be maintained at. As you can see, when P is low, at the beginning of growth, the ratio P/K is sufficiently small such that C is approximately equal to 1. When P is close to K, the ratio P/K is approximately equal to 1, so C approaches 0.
Let's call the function C(P) the "logistic coefficient". And thus we have the logistic equation...
...which was first published by Dutch mathematical biologist Pierre Verhulst around 1845. The logistic differential equation separable, and thus we can derive an explicit analytical solution.
So by rearranging and separating, we get...
On the left hand side, we can separate the term into partial fractions...
And thus we can rewrite the differential equation and integrate both sides...
And thus we have derived the general solution for the logistic differential equation.
Ok, we'll leave it here for now. In the next tutorial, we will look at a specific example of applying the logistic equation to model the progressive growth of a population.
Below is a list of tutorials I've created so far on the subject of Differential Equations:
First-Order Differential Equations with Separable Variables - Example 1
Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky
The Logistic Model for Population Growth
Please give me an Upvote and Resteem if you have found this tutorial helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
I would really appreciate any small donation which will help me to help more math students of the world.
Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu
Great post on applications of differential equations. This is very useful in various fields such as ecology, biology, machine learning, chemistry, neural networks, medicine, physics and many more.
Thank you @mathfortress. Good to see another mathematician on Steemit!
Very nice, thank you
Thanks for stopping by!
@originalworks
The @OriginalWorks bot has determined this post by @masterwu to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!