In part 1 I covered my initial idea, which I failed to complete. Now I'll cover my submission - Mindbender
Failing is fine
Failing to make your intial jam idea is fine, it happened to me in the past, and I had a really nice result regardless. In fact, it is one of the better games I've made.
This time was no different, I had a big idea, and I didn't have the time, and couldn't connect the working pieces. I came up with an alternate idea, one that I could definitely do in the remaining time.
Non-euclidean space
The first time I've encountered non-euclidean space was in the game Antichamber. I liked the idea of not really knowing the rules of the world and having to discover them, unfortunately "walking simulator" type games make me nauseous. Couldn't finish it, and couldn't finish The Stanley Parable either. Though I recommend giving both a try.
Antichamber kind of sparked my interest in it, but it was HyperRogue that really got me interested in it, mostly because it was 2D, which is my preference when making, and playing, games. HyperRogue implemnets a hyperbolic plane, it connects more rooms than are possible to connect on a plane, the geometry would never work in a 2D space, but by stretching and shrinking the horizons, you can make it look like it works. The 2D space in hyperrogue can be displayed, with some trickery, but I felt there wasn't any point in trying to do that. I wanted a non-euclidean maze, and I would make it so only the connecting rooms are visible.
This endeavor was actually a pretty cool experience from a programming perspective, so I'm going to throw in some algorithmic ideas here. You can follow along even if you don't know how to code, but if you don't want to, you can skip ahead to "What else can be done?" to read about other ideas I've had.
Coding fun!
So the first thing I wanted to do is not break the player. Yes, I want to introduce them to some unknown, but not break them complete. If I made a hyperbolic plane from square rooms, it would look something like this:

If you stand in a room in the center, and take a left, you would need to do so 5 times to get back to the same room.
So I decided on some ground rules, to keep the player sane.
Rooms will always retain their orientation, top is top, and bottom is bottom.
Rooms will always connect to the opposite side of another room, the left side of one room will connect to the right side of another room.
This will keep players from completely losing all sense of direction. Downside is, that this increases connectivity, which isn't something very desirable in a maze. Because of this, I decided that instead of "find your way out" I will make a maze that would require going through all rooms.
My starting algorithm was very simple, start with a root room, then create more rooms and attach it to one of the existing rooms in any direction that is unoccupied. This will make sure that you have a way to reach every room from the root room.
This however would make it extremely obvious to visit all rooms, so why not add some further connectivity. I iterate over all the rooms and randomly connect them to more rooms, sometimes even to themselves. Connecting the left side of a room to the right side of the same room is fun.
I played around with this maze a bit, and soon figured out it's a bit too easy to visit all the rooms, since they are hyperconnected, so I added a level of difficulty. Go through all the rooms without going through the same room twice.
This makes for an interesting puzzle. I could play around more with the amount of connectivity I add, see what makes the most interesting puzzle. As always, it's never the extreme. Full connectivity and least amount of connectivity both make it too easy. Need some moderation.
What else can be done?
I've wondered what other games could be played on this non-euclidean maze, and the first two that popped into my mind were Snake, and Sokoban.
Problem with both though, is that they're very hard to play without seeing the entire map, and well, I have no idea how I would display that map. It could be displayed as a sort of graph.
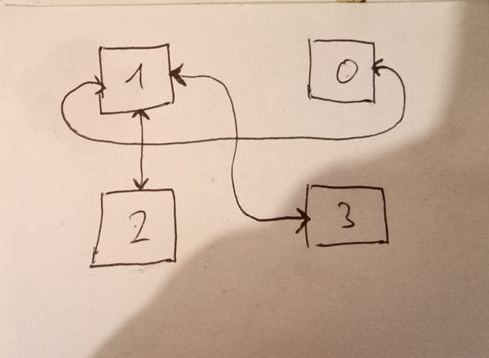
But really, who wants to look at that mindbendy thing.
Other options would be to find keys to open doors, which would be a bit more interesting I think, so it'll have more of a sense of exploration.
Another option is have a simon says kind of game, where you are shown a sequence of colors, and you need to pass through the rooms in that sequence of colors. Could be fun? no idea.
Summary
I enjoyed playing with non-euclidean geometry, and I enjoyed the theme of this jam.
I'd like to explore some non-euclidean geometry games, but I'll need to bite the bullet and find a way to display them more coherently to the player. At least, for a 2D game.
Thanks to @loomy for running it. If you're interested in joining the jam, it's held on the first Friday of every month, and you can follow @loomy or @steemitjam for updates.
Next up I'm going to take the time to play the other two entries, and write about them.
