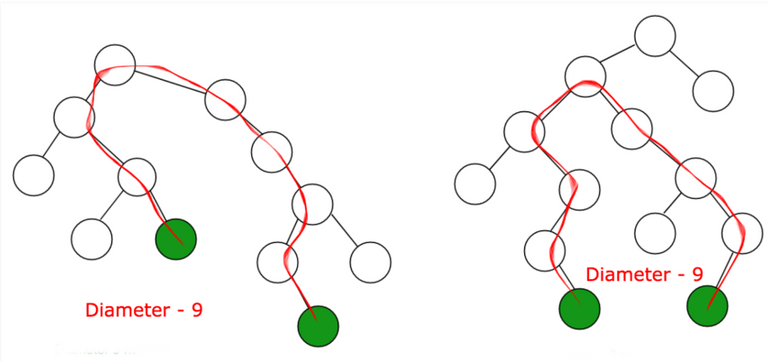
Problem statement:-
Given a binary tree, you need to compute the length of the diameter of the tree. The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.
Example:
Given a binary tree
1
/ \
2 3
/ \
4 5
Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].
Note: The length of path between two nodes is represented by the number of edges between them.
Algorithm:-
The diameter of binary tree can be defined as max(Length of left subtree, Length of right subtree, Longest path between two nodes that passes through the root).
Steps:-
- Find the height of left subtree.
- Find the height of right subtree.
- Find the left diameter.
- Find the right diameter.
- Return the Maximum(Diameter of left subtree, Diameter of right subtree, Longest path between two nodes which passes through the root.)
Option 1:- O(N2) time complexity
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public: int findDiameter(TreeNode * root, int & h) {
if (root == NULL) {
h = 0;
return 0;
}
int h1 = 0, h2 = 0;
int d1 = findDiameter(root -> left, h1);
int d2 = findDiameter(root -> right, h2);
h = max(h1, h2) + 1;
return max(h1 + h2, max(d1, d2));
}
int diameterOfBinaryTree(TreeNode * root) {
if (root == NULL) return 0;
int h;
return findDiameter(root, h);
}
};
Option 2:- O(N) time complexity
In below example, we are doing 2 things in one pass , viz. finding the heights of left and right subtrees , computing the max of the left and right heights combined and returning the max of left and right subtree heights + 1 (for the root node)
class Solution {
public: int diameterOfBinaryTree(TreeNode * root) {
int diameter = 0;
depth(root, diameter);
return diameter;
}
private: int depth(TreeNode * root, int & diameter) {
if (!root) return 0;
int left = depth(root - > left, diameter);
int right = depth(root - > right, diameter);
diameter = max(diameter, left + right);
return max(left, right) + 1;
}
};
Posted from my blog with SteemPress : https://www.golibrary.co/finding-diameter-of-a-binary-tree/
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
https://www.geeksforgeeks.org/diameter-of-a-binary-tree/