Ecuaciones no Lineales y Optimización | 6ta Parte

[abdulmath]

Saludos queridos lectores, bienvenidos nuevamente a mi Blog. En la ciencia, como en la Ingeniería, las ecuaciones no lineales, es un tema de gran interés, ya que las mayoría de los fenómenos físicos o de la vida real, están modelados por ecuaciones no lineales; estos fenómenos naturales por lo general se dicen que están fuera de equilibrio es estos casos y las ecuaciones dependerán de la naturaleza del fenómeno, es decir, discretas o continuas, en cuyos casos se representan por mapeo o ecuaciones diferenciales respectivamente. En esta publicación continuaremos tratando el tema de las Ecuaciones no Lineales y Optimización, en su quinta entrega. En esta ocasión desarrollaremos algunos aspectos sobre la mínimización de las funciones multivaluadas, y como desarrollar los script, la función objetivo y mucho más para que puedan trabajar con ellos si es de su interés profesional. La misma está dirigida a profesionales e investigadores con algunas destrezas en temas de análisis real, cálculo avanzado, entre otros. Al final, les dejare una corta bibliografía, donde podrán consultar algunos tópicos especiales para los interesados. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.

La función vectorial

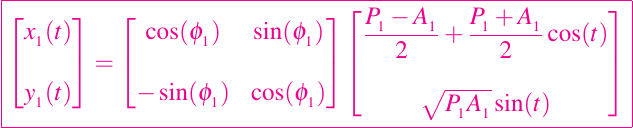
describe una órbita elíptica inclinada con un foco en (0, 0). Pensemos en el Sol como si estuviera situado en este punto. El parámetro φ₁ es el ángulo de inclinación. Si A₁ es mayor o igual que P₁, entonces A₁ y P₁ son las distancias máximas y mínimas entre el Sol y la órbita. Sea


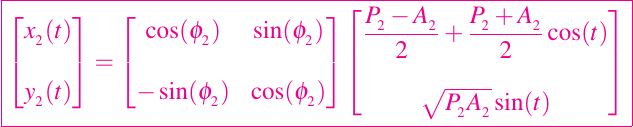
una segunda órbita de este tipo y la cual podemos visualizar en la gráfica siguiente.


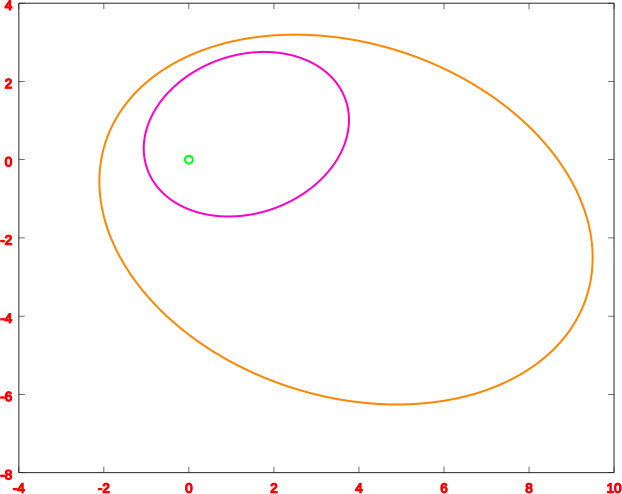
_{Gráfico de las órbitas. Elaborado con GNU Octave, por @abdulmath.}
donde (A₁, P₁, φ₁) = (10, 2, pi/8), y (A₂, P₂, φ₂) = (10, 2, pi/8).

Nuestro objetivo es encontrar la distancia mínima desde un punto en la primera órbita (A₁, P₁, φ₁) hasta un punto en la segunda órbita (A₂, P₂, φ₂). Para una medida de distancia, utilizamos la siguiente función

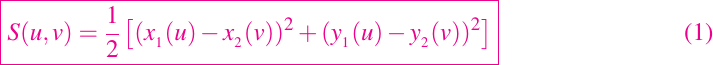
Esta es una función de dos variables, y de acuerdo como lo vimos en la publiación anterior (Ecuaciones no Lineales y Optimización | 5ta Parte), la función S es la función objetivo. Notemos que t₁ es un punto seleccionado en la órbita exterior y t₂ es un punto seleccionado la órbita interior. A continuación estudiaremos la mínimización de funciones multivaluadas como S(t).

---

---

La implementación de S(t) depende de otra función que llamaremos orbita, la cual mostramos a continuación:

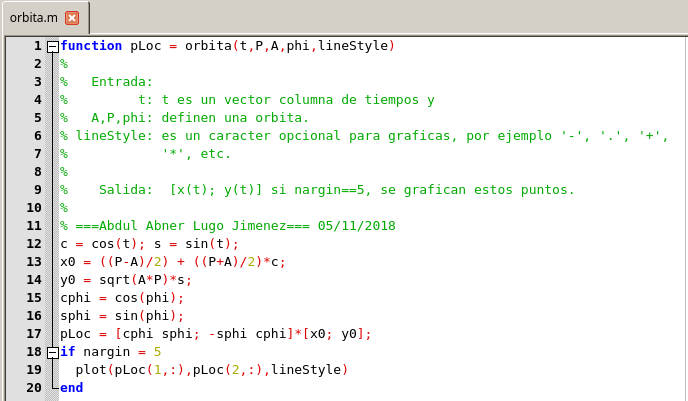
_{Función orbita. Elaborada con GNU Octave, por @abdulmath.}

Con esta función podemos fácilmente generar y gráficas y puntos en las órbitas. El script siguiente gráfica dos órbitas y traza una línea que conecta el punto t₁ = 3 en la primera órbita con el punto t₂ = 4 en la segunda órbita.

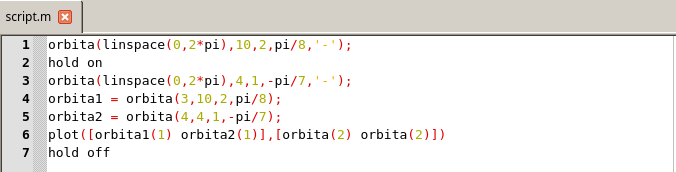
_{Script usando para gráficas las órbitas. Elaborada con GNU Octave, por @abdulmath.}

La separación entre estos dos puntos es una función de un vector de dos variables independientes y los parámetros A₁, P₁, φ₁, A₂, P₂, φ₂, el cual visualizamos en el siguiente funcion:

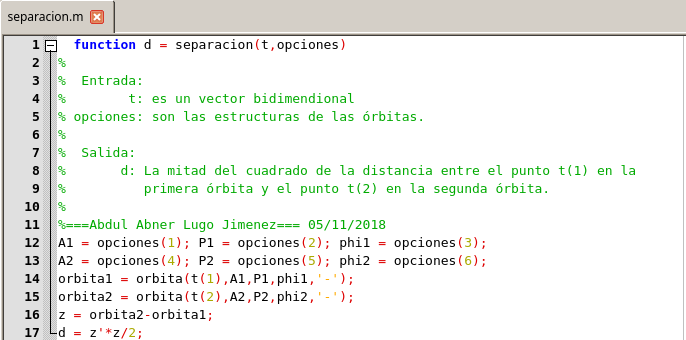
_{Función separacion. Elaborado en GNU Octave, por @abdulmath.}
Observemos cómo se empaquetan los parámetros de órbita en un vector de dimensión 6, y usando el siguiente script a continuación podemos ver como usamos la función que acabamos de mostrar separacion


_{Script para calcular la separación de las órbitas. Elaborado en GNU Octave, por @abdulmath.}
asigna a d el valor


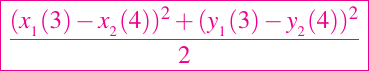
con

---

---

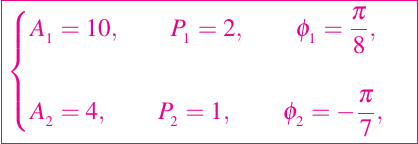
Supongamos que una persona se encuentra en un lugar nublado, y parada en una ladera sin un mapa. Si esta persona quiere dar un paso coherente con el objetivo de alcanzar de un valle, es razonable dar ese paso en la dirección más cuesta abajo. Matemáticamente, este hecho, dirigirse en la dirección del gradiente negativo.

Recordemos que el gradiente de una función

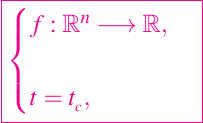
es un vector de derivadas parciales:


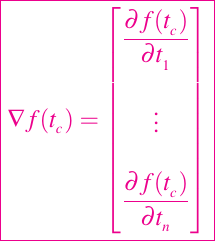
El gradiente siempre apunta en la dirección del mayor incremento y su negación apunta en la dirección de la mayor disminución. Tomando las parciales en t₁ y t₂ en la ecuación dada en (1), vemos que


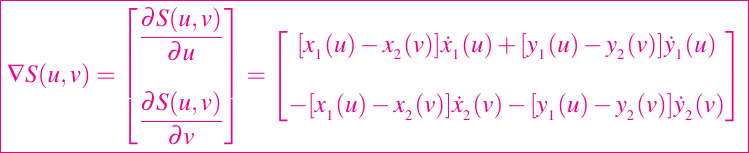
Sustituyendo las definiciones de las funciones de las componentes, llegamos a la siguiente implementación del gradiente:


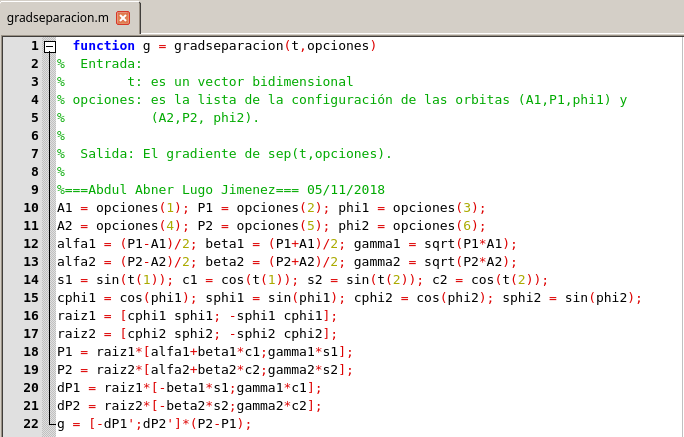
_{Función para calcular el gradiente de la función separacion. Elaborado con GNU Octave, por @abdulmath.}
La derivación no es importante. Pero lo que es importante es apreciar que la implementación de la función gradiente puede ser muy complicada y consumir mucho tiempo. Nuestro problema es pequeño (n = 2) y simple. Para aplicaciones de alta dimensión con funciones objetivas complicadas, a menudo es necesario usar algunos paquetes de diferenciación simbólica.

---

---

A partir de la teoría de aproximación de Taylor multivalorada, sabemos que si λ_c es real y s_c es un n-vector, entonces

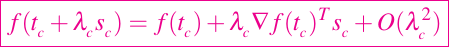
Por lo tanto, podemos esperar una disminución en el valor de f si establecemos que la dirección del paso s_c sea


y el parámetro de longitud de paso λ_c para que sea lo suficientemente pequeño. Si el gradiente es cero, entonces este argumento se rompe. En ese caso t_c es un punto crítico, pero puede no ser un mínimo local. Nuestra búsqueda del fondo del valle puede estancarse en ese lugar.

La determinación práctica de λ_c es el problema de la búsqueda de línea. Idealmente, nos gustaría minimizar f(t_c + λ_cs_c) sobre todo λ . Sin embargo, una solución aproximada a este problema de minimización unidimensional suele ser lo suficientemente buena y a menudo esencial si f es muy costosa de evaluar. Esto nos lleva al marco de descenso más empinado para calcular una mejora t₊ al minimizador actual:

• calcular el gradiente
  
  
  y sea s_c = - g_c.
• Elegir a bajo costo λ_c tal que f(t_c + λ_cs_c) es suficientemente pequeña como f(t_c).
• Sea t₊ = t_c + λ_cs_c.

El diseño de una estrategia razonable de búsqueda de líneas es una tarea no trivial.

---

---

Queridos amigos y lectores, espero hayan disfrutado de esta segunda entrega de este tan apasionante e interesante tema del cálculo numérico, Ecuaciones no Lineales y Optimización | 6ta Parte apoyado con el entorno GNU Octave, en esta oportunidad pudimos estudiar algunas detalles o aspectos importantes, acerca de la minimización de funciones multivaloradas. Espero que el mismo sea de apoyo a ustedes en sus trabajos, o quizás sirva de apoyo para sus hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

• Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
• Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
• Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, GNU Octave, , GIMP e Inkscape.

---

---

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

Comments

[ramonycajal]

[abdulmath]

Muchas gracias por el apoyo. Muy agradecido.

Saludos y Éxitos

[yetzysavir]

Bueno debo decirte que aunque lo mio no son las matemáticas, debo felicitarte por tu gran trabajo mi amor, muy buena tu explicación. Besos y saludos.

[abdulmath]

Muchas gracias cariño, es bueno que tengas una buena apreciación de mis aportes. Y que hayas tenido el tiempo de leerla.

Saludos y un abrazo.

[sandrag89]

Woou sin duda es impresionante tu capacidad de comprender las matematicas. Gracias por darle valor a la comunidad hispana con tu contenido.

[abdulmath]

Hola @sandrag89, muchas gracias por tus comentarios. Trato cada día de dar un pequeño aporte a todos los que se interesen por tan bonitos temas (para mi gusto).

Saludos Cordiales.

[minnowsupport]

Congratulations! This post has been upvoted from the communal account, @minnowsupport, by abdulmath from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.

If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.

[steemstem]

This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.

If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!

For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!