Tópicos Especiales de Interpolación Polinomial
Siguiendo con el tema de Interpolación Polinomial que hemos venido desarrollando, vamos a tratar algunos tópicos especiales donde hablaremos de propiedades y algoritmos asociados con diferencias divididas, la noción de interpolación inversa y los conceptos básicos de la interpolación lineal bidimensional.
Diferencias Divididas
Consideremos una vez más el problema de interpolar cuatro puntos, es decir, n = 4, entonces podemos expresar a las constantes c1, c2, c3 y c4 en términos de xi y f:
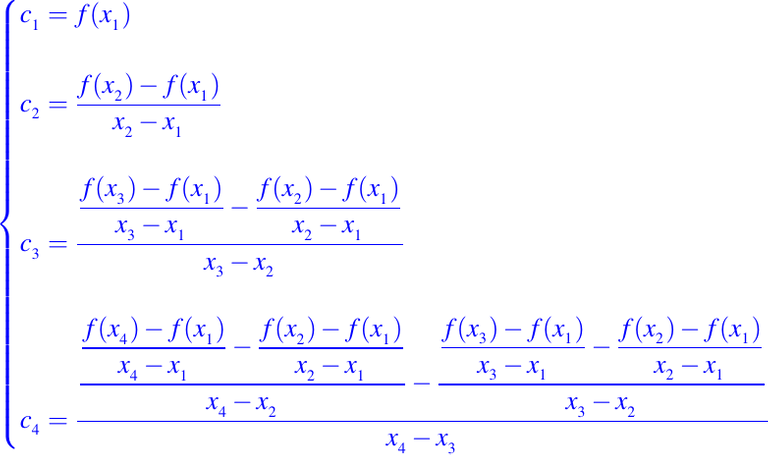
Los coeficientes los conocemos como diferencias divididas. Para enfatizar la dependencia de las constantes ck en f y x1, x2, . . . ,xk, escribimos
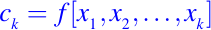
y se refieren a esta cantidad como diferencia dividida de k - 1 orden. Así
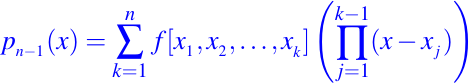
es el polinomio interpolante de n puntos de f en x1, x2, . . . ,xn,
Ahora establecemos otra propiedad recursiva que relaciona las diferencias divididas de f en los subconjuntos designados de {x1, . . . , xn}. Supongamos que pL(x) y pR(x) son los interpolantes de f en {x1, . . . , xk - 1} y {x2, . . . , xk}, respectivamente. Es fácil verificar que si
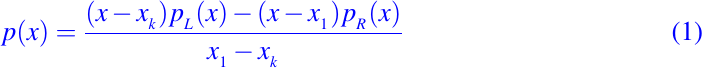
entonces p(xi)=f(xi), i = 1:n. Así p(x) es el interpolante de f en {x1, . . . , xk} y entonces

Notemos que
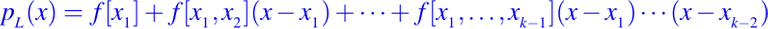
el coeficiente de xk - 2 esta dado por f[x1, . . . , xk - 1]. Del mismo modo,

el coeficiente de xk - 2 esta dado por f[x2, . . . , xk]. Comparando los coeficientes de xk - 1 en (1) y (2) concluimos que
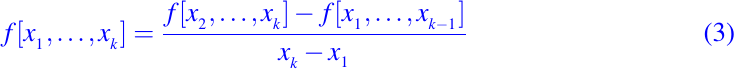
El desarrollo de diferencias divididas de orden superior a partir de diferencias divididas de orden inferior se ilustra a continuación
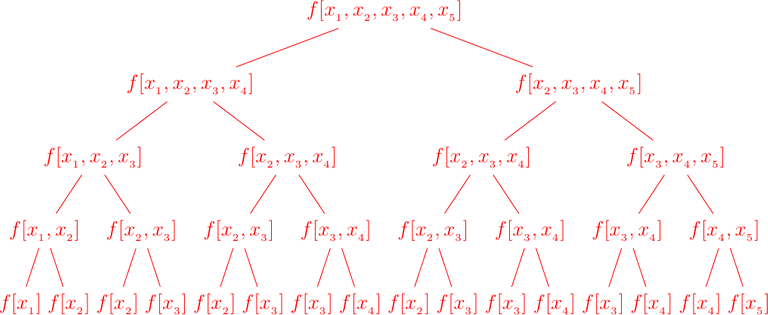
Esquema Diferencias Divididas.
Observemos que las diferencias divididas que buscamos están a lo largo del borde izquierdo del árbol. Al quitar el exceso, vemos que las diferencias divididas requeridas se pueden construir como se muestra a continuación

Esquema de cálculo eficiente de Diferencias Divididas.
Esto nos permite escribir la siguiente función en Octave de la siguiente manera:
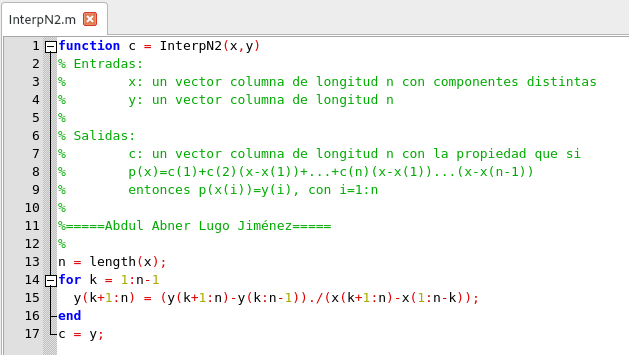
Función para la Interpolación de Newton optimizada. Elaborado por @abdulmath con GNU Octave.
Un numéro de simplificaciones resultan si xi son igualmente espaciados. Asumimos que

donde h > 0 es el espaciado. De la ecuación (3) vemos que
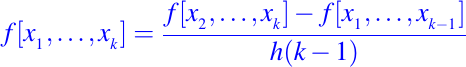
Esto hace que la diferencia dividida sea un ajuste de las diferencias
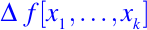
que definimos de la siguiente manera
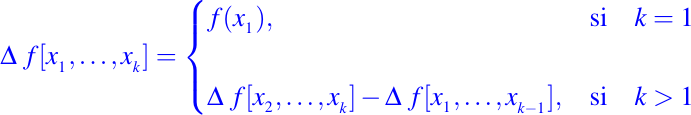
Por ejemplo,
| Orden 0 | Orden 1 | Orden 2 | Orden 3 | Orden 4 |
| f1 | ||||
| f2 | f2 - f1 | |||
| f3 | f3 - f2 | f3 -2f2+f1 | ||
| f4 | f4 - f3 | f4 -2f3+f2 | f4 -3f3+3f2-f1 | |
| f5 | f5 - f4 | f5 -2f4+f3 | f5 -3f4+3f3-f2 | f5 -4f4+6f3-4f2+f1 |
No es dificil mostrar que
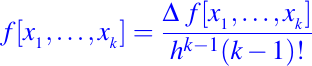
La función incorporada
diff se puede usar para calcular diferencias. En particular, si y es un vector de n componentes, entoncesd = diff(y)y
d = y(2:n) - y(1:n-1)son equivalentes.
Un segundo argumento se puede usar para calcular las diferencias de orden superior. Por ejemplo,
d = diff(y,2)calcula las diferencias de segundo orden:
d = y(3:n) - 2*y(2:n-1) + y(1:n-2)
Interpolación Inversa
Supongamos que la función f(x) tiene una inversa en [a, b]. Esto significa que existe una función g(x) tal que f(g(x)) = x para todo x en [a, b]. Por lo tanto, si g(x) = x1/2 la función inversa es f(x) = x2 en [0, 1]. Si

y yi = f(xi), entonces el polinomio que interpola los datos (yi, xi), i = 1:n es una interpolador de la inversa de f. Así tenemos el siguiente script
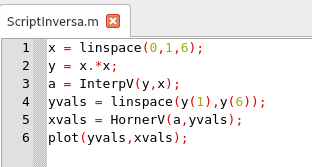
Script para interpolar la inversa de f(x). Elaborado por @abdulmath, en GNU Octave
el mismo gráfica un interpolador de orden 5 de la función raíz cuadrada. Esto es lo que conocemos interpolación inversa, y una de sus aplicaciones importantes, es para hallar los ceros de una función.
Supongamos que f(x) es una función continua y monótona creciente o decreciente en [a, b]. Si f(a)f(b)<0 entonces f(x) tiene un cero en [a, b]. Si g(y) es un interpolador inverso, entonces g(0) podemos considerarlo como una aproximación de una raíz de la función.

Interpolación en 2 Dimensiones
Supongamos que (u, v) esta dentro del rectangulo
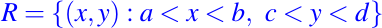
Supongamos que f(x, y) esta definida en R y que sus valores en las cuatro esquinas fac = f(a, c), fbc = f(b, c), fad = f(a, d), y fbd = f(b, d). Nuestro objetivo es usar un interpolador lineal para obtener una estimación de f(u, v). Supongamos que h esta en el intervalo [0, 1] con la propiedad que u = (1-h)a + hb. Resulta que
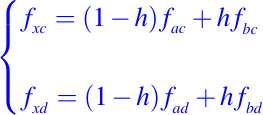
son estimaciones interpoladas linealmente de f(u, c) y f(u, d) respectivamente. En consecuencia, si s está en el intervalo [0, 1] con v = (1 - s)c + sd, entonces una segunda interpolación entre f1 y f2 da una estimación de f(u, v):

Juntando todo, vemos que
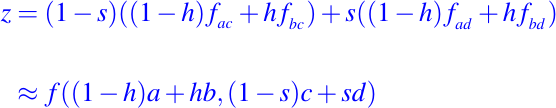
La siguiente figura nos muestra los puntos de interpolación.
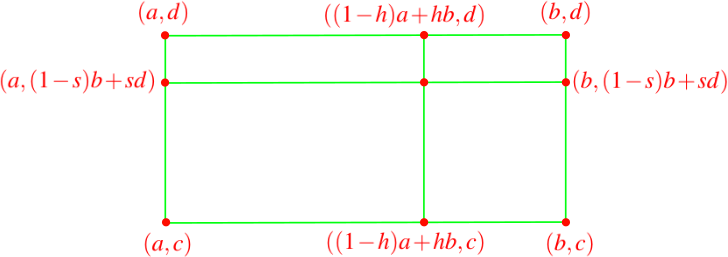
Interpolación lineal en dos dimensiones.
Para probar estas ideas, escribimos una función que almacena en una matriz los valores de una función específica de dos variables:
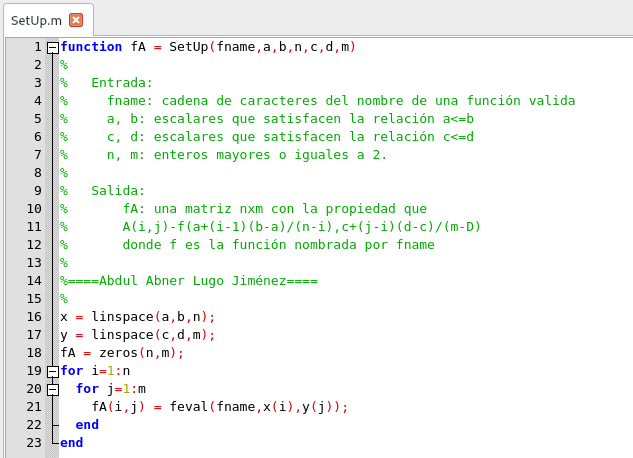
Función de almacenamiento de los valores de f(x, y). Elaborado por @abdulmath con GNU Octave
En general, la función pasada como
feval puede tener un número arbitrario de argumentos. Si n son necesitados, entonces estos deben ser especificados e la llamada de la función feval. Para interpolar los valores en una matriz calculada por SetUp, es necesario "localizar" el punto en el cual la interpolación es requerida. Los cuatro valores relevantes de la matriz deben combinarse como se describió anteriormente.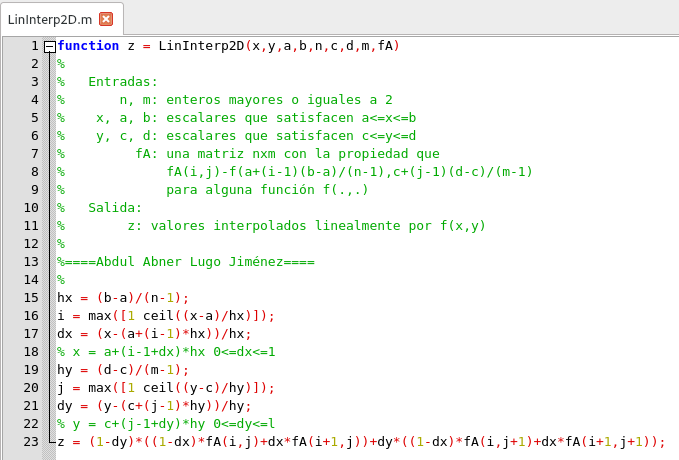
Función de Interpolación Lineal en dos dimensiones

Queridos amigos y lectores, espero hayan disfrutado y aprendido acerca de la Interpolación Polinomial usando el entorno GNU Octave | 2ra Parte y ultima acerca de este tema. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
- Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
- Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.
También los invito a leer las anteriores publicaciones de está serie de Introducción a las Ecuaciones Diferenciales Parciales, que estoy seguro serán de su interés:
| Interpolación Polinomial usando el entorno GNU Octave - 1era Parte. | Interpolación Polinomial usando el entorno GNU Octave - 2da Parte. |
|---|
Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, GNU Octave,  , GIMP e Inkscape.
, GIMP e Inkscape.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

Imagen diseñada con GIMP y elaborada por @abdulmath.
¡Felicitaciones!
Estas participando para optar a la mención especial, que se efectuará el 26 de Agosto del 2018 a las 8:00 pm (hora de Venezuela); donde el autor del artículo seleccionado recibirá la cantidad de 1 SBD transferidos a su cuenta.
Contáctanos en Discord: https://discord.gg/hkCjFeb
Apoya al trail de entropía y así podrás ganar recompensas de curación de forma automática, entra aquí para más información sobre nuestro TRAIL.
Puedes consultar el reporte diario de curación visitando @entropia
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Muchas gracias por el apoyo a mi trabajo.
Normalmente usamos la extrapolación en la mayoría de las investigaciones científicas, pero también es importante conocer la función de interpolación lineal o en este caso polinomial. Buen trabajo mi estimado @abdulmath
Lo que comentas es muy cierto, la interpolación polinomial es un tema de importancia, pero que para algunos casos no es tan útil, dependiendo del caso de estudio. Agradecido por tu comentario y pasar a visitar mi blog. Saludos y un abrazo fraterno @iamphysical
Congratulations @abdulmath! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPThis post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Thanks for the support
Hi @abdulmath!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Thanks for the support
Hola @selenyta, muy agradecido por tus lindos y apreciados comentarios. Pues la física y la matemática son dos ciencias hermanas que se retroalimentan constantemente. Saludos y un abrazo.