Esta publicación esta dirigida a estudiantes, profesionales e investigadores en específico en el área de las Matemáticas Aplicadas e Ingeniería, y público interesado en estos temas interesantes para el entendimiento de buena parte del medio que nos rodea día a día. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.
= (
, 
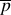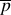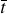, Re), y si posee una expansión asintótica en potencias de Re, entonces
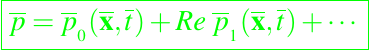
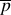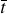(, , Re)Re cerca de Re = 0
En tal situación la expansión es singular, y se debe adoptar un procedimiento de perturbación singular. Un ejemplo es el problema visto en la publicación anterior (Modelos matemáticos aplicados a la Mécanica Aplicada - Introducción) cuando Re >> 1 de modo que una expansión regular sea potencia de 1/Re. Cuando 1/Re se toma igual a cero, el orden de la ecuación se reduce porque el término con derivada más alta desaparece y no todas las condiciones de contorno pueden ser satisfechas. Una declaración alternativa es que, adyacente a la abundancia en la que q es dada, algunos derivadas de q serán no acotadas y se crea una capa límite en la que las derivadas de q son grandes y el término omitido debe ser conservado.
El problema es determinar las constantes que describen la reacción, es decir, el calor de la reacción λ, la energía de activación E y la constante de velocidad A∗, a partir de estas observaciones. Para simplificar, consideramos sólo una única reacción de primer orden con una constante de velocidad, de modo que si α(t) es la fracción de masa del material activo, entonces de la Ley de Arrhenius
donde R es una constante conocida y T es la temperatura absoluta. También, por simplicidad, consideramos un modelo unidimensional, es decir, la muestra es un bloque infinito de ancho 2L, calentado por ambos lados sin transferencia de calor paralela a sus lados. Entonces α es una función de x y t y la derivada con respecto al tiempo en la ecuación (1) es la derivada parcial
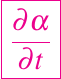
La reacción química, cuando ocurre, crea calor en la muestra de manera que un balance de energía o calor, da como resultado
Las condiciones de frontera son tal que no se haya producido ninguna reacción en t = 0 de modo que α = 1, y α es mayor o igual a cero, para todos los valores de t. También T = T0 cuando t = 0, y si suponemos una situación simétrica
Para el calentamiento debido al horno en x = L, un modelo simple es suponer que se conoce un coeficiente de transferencia de calor h∗ desde el horno a la muestra de modo que
donde TF es la temperatura prescrita del horno. De nuevo, para simplificar, consideramos un problema en el que el horno se calienta a una velocidad uniforme de β, de modo que TF(t) = T0 + βt donde β es conocido y puede ser variado.
Un perfil de temperatura típico que se observa en la práctica lo podemos ve en la figura siguiente
Perfil de Temperatura típico. Elaborado por @abdulmath en Inkscape.
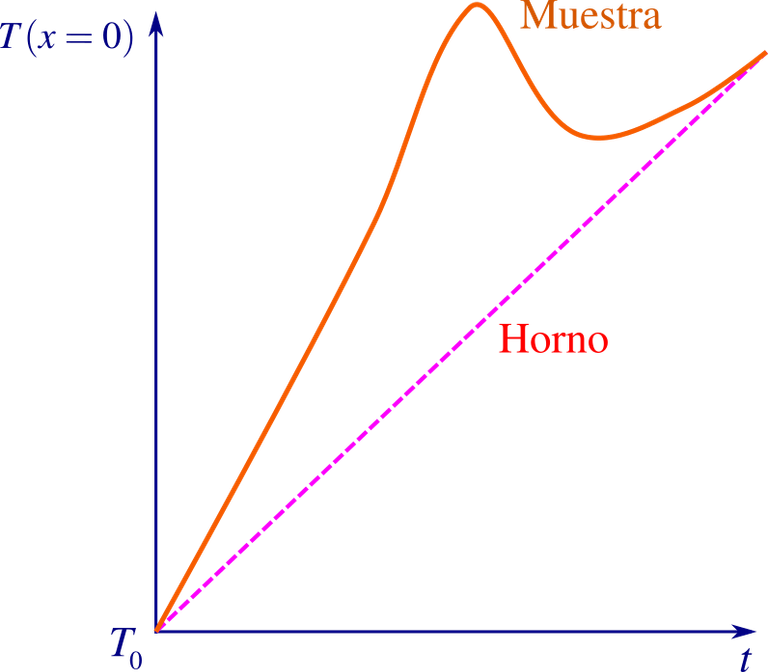
la primera tarea es determinar para qué rango de valores de las constantes podría predecirse dicho perfil mediante el modelo matemático. Para ello, primero normalizamos el problema, escalando las variables x con L, t con el tiempo de conducción L2/κ2, y T - T0 con λ/c. Las ecuaciones (2) y (1) se expresan ahora utilizando variables escaladas:
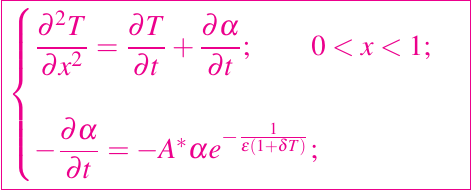
donde
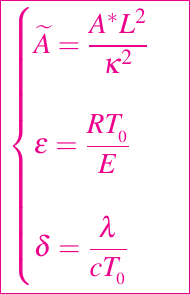
Las condiciones de contorno son
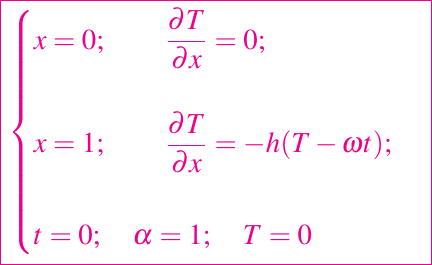
donde
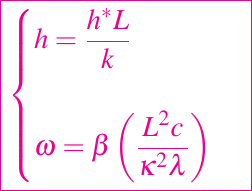
Hay cinco parámetros no dimensionales, tres de los cuales son constantes desconocidas, h dada, y ω que no se conoce pero que puede ser variable. Si todos ellos son de orden uno, el problema es claramente difícil y se puede avanzar muy poco en su análisis. Por lo tanto, consideramos las implicaciones de una situación en la que el ω << 1, es decir, el horno sólo se calienta lentamente en comparación con el tiempo de conducción. Para que el término de calentamiento del horno aparezca en las ecuaciones en el límite ω tiende a cero, el tiempo tiene que ser reescalado, así que finalmente escribimos τ = ωt para obtener un problema de valor en la frontera
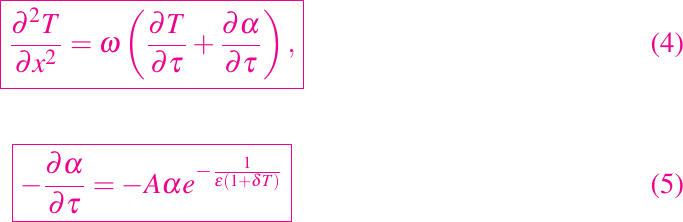
donde
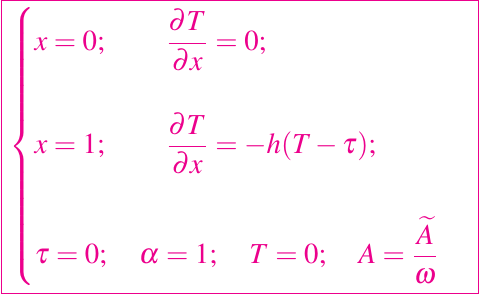
Ahora buscamos una expansión regular de T y de α en potencias de ω, y para mantener una relación no trivial para α requerimos que A sea de orden uno, y por lo tanto A es pequeño. Una simple integración da como resultado
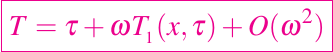
y por lo tanto
donde
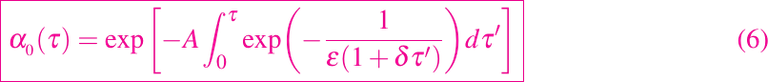
Sustituyendo estas expresiones en la ecuación (4) y omitiendo O(ω2) obtenemos:
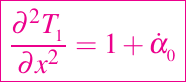
con condiciones de frontera
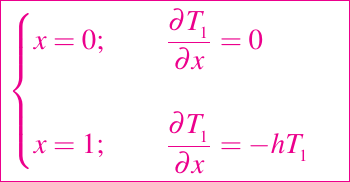
Desde una mayor integración
Esto da una expansión consistente para T si las constantes implicadas son todas de orden uno, excepto cerca de τ = 0 donde la condición de contorno T = 0 no se ha cumplido. Sin embargo, se satisfe α = 1 y podríamos reescalar para valores de τ pequeños con α = 1 para compensar esta deficiencia; sin embargo, no es de gran interés ya que en tales momentos la reacción apenas ha comenzado. La cuestión de interés es si la ecuación dada en (7) nos da una curva para T en x = 0 de la forma general mostrada en la figura mostarada anteriormente; es decir, si se pueden elegir las constantes A, ε y δ para que los resultados observados se ajusten por
Esta es una expresión bastante formidable que puede simplificarse, y aún así tener un perfil adecuado, en el caso de energía de activación pequeña y calor de reacción, es decir, ε y δ ambos de valores pequeños.
En general, sin embargo, se pueden construir perfiles para Tx = 0 - τ que tienen un valor máximo ωTm en τ = τm. Estos valores se miden fácilmente a partir de la evidencia experimental, y proporcionan dos relaciones que conectan las incógnitas A, ε y δ.
Queridos amigos y lectores, espero hayan disfrutado de una nueva publicación donde las matemáticas tienen sus aplicaciones en otros campos de la ciencia los cuales son de mucho interés en general. Espero que la misma haya sido de su agrado, y pueda servir de una ventana de apoyo para visualizar las estrechas relaciones que existen en particular entre las ciencias, así como se puede contextualizar las mismas teorías en la ingeniería, gracias por tomar un poco de su tiempo y poder disfrutar un poco más del maravilloso mundo de las matemáticas y las ciencias básicas. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Bender, C. M. and Orszag, S. A. Advanced mathematical methods for scientists and engineers. McGraw-Hill, New York. 1978.
- Courant, R. and Hilbert, D. Methods of mathematical physics, vol. I. Interscience, New York. 1976.
- Landau, L. D. and Lifshitz, E. M. Fluid mechanics. Pergamon, London. 1963.
- Stakgold, I. Green's functions and boundary value problems. Wiley-Interscience, New York. 1979.
La imagen de fondo de la portada es una imagen de libre uso tomada de 
@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.
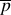(y también 
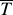y 
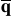) en el ejemplo depresentamos en la publicación ( es entonces 
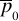, y se pueden obtener sucesivamente términos de orden superior. Este es un procedimiento de perturbación regular y puede ser usado si (y también 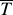y 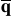) son funciones regulares de . Sin embargo, esto casi siempre no se sabe de antemano y el enfoque adoptado es intentar realizar una expansión regular y esperar que si no es válida habrá una clara inconsistencia en los primeros términos de la expansión. Esta inconsistencia puede surgir en la forma del problema para 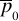esté mal planteado, como sucedió antes de que 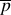fuera reescalado cuando no existia una solución para 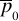. Alternativamente, las soluciones obtenidas pueden no estar limitadas en alguna región de las variables de espacio y tiempo y .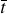
Excelente post, llamativo y pues si soy una a las que las matemáticas les da temor, menos mal ya pase todas las mates. Me llama la atención de este grupo de ciencias, por mi parte escribo sobre biología principalmente debido a mi carrera y experiencias en el laboratorio donde hago tesis. Un saludo.
Hola @vivokiwi, estas invitada a participar y a escribir acerca de biología, pasate por el canal de discord e intereactua por allá. Saludos espero pronto verte por allá compartiendo. Saludos cordiales
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
¡Felicitaciones!
Te participamos que puedes invertir en el PROYECTO ENTROPÍA mediante tu delegación de Steem Power y así comenzar a recibir ganancias de forma semanal transferidas automáticamente a tu monedero todos los lunes. Entra aquí para más información sobre cómo invertir en ENTROPÍA.
Entra aquí para más información sobre nuestro trail.Apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática.
Puedes consultar el reporte diario de curación visitando @entropia.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.Congratulations! This post has been upvoted from the communal account, @minnowsupport, by abdulmath from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Simplemente genial eres un genio.
Gracias amigo por tu valoración @stop40. Saludos y un abrazo.