Mathematical induction: Proving Gauss sum formula right

[aximot]

Hi everyone :)

Carl Friedrich Gauss (1777-1855), also called "the foremost of mathematicians", was once asked to add up the first 100 integers as a punishment during his elementary school time. Wolfgang Sartorius von Waltershausen (1809–1876) mentioned, Gauss was able to finish the task within seconds. Even though, we don't know if this story is really true, we know that the math behind it, is. 

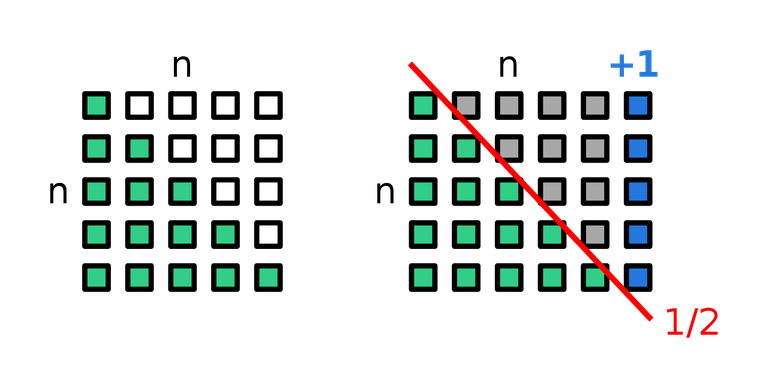
the geometric interpretation of the method

By splitting the numbers from 1-50 and 51-100, we can already see while the upper row increases in value, the lower decreases by he same amount. The result of an addition is constantly the same:

1      2    3   4    5 ... 48 49 50

100 99 98 97 96... 51 52 53

100+1=101

2+99=101

2+98=101

...

Adding up the first 100 integers, pairs of the sum "101" can be formed. As there are 50 pairs (100 numbers,  pairs= 100/2=50), each with the sum of 101 as shown above, the result is: 50*101= 5050. This brilliant strategy was probably used by young Gauss in his school lesson back in the days.

But how can this relate to mathematical induction?

Mathematical induction is a method of proving a statement true for every natural number bigger or equal to the starting value. It is easy to imagine it as a row of dominos. If we want to get them fall, two conditions have to be secured. The first domino has to fall and every other stone has to push the following one. In this case, the first stone is the smallest natural number (1). Another domino is the same as a random number n. Because stone n has to cause the fall of the next stone, the case n+1 has to be proven right, too. 

If we use the following formula:

n*(n+1)/2

How do we know, if it is right for every step of the sum from 1-100? We could add up all numbers and compare it to the result of the equation, but instead of testing it for every number, a much more efficient method is available:

Step 1: The basic case

First, the basic case is important. It is used to prove the statement right for the smallest number. Hence number 1 is the smallest natural number in this definition, we use it to prove:

The sum from 1 to 1 =1. Putting in 1 for n, we get 2/2=1.

As both sides are equal (1=1), the statement for n=1 is true. This calculation could be done with every other number from 1-100 too, but instead of wasting too much time, the next step plays out.

Step 2: The inductive hypothesis & the induction step

For the inductive hypothesis, we pick a random number declared with the variable n. Instead of using a specific natural number as above, we choose the general case for a random number n now. Looking at our dominoe example again, we pick a random stone in the row now.

The last step is the inductive step, where the statement is getting  proven for n+1 too. We put in (n+1) now for n and by replacing it, we receive the following equation:

Now we can use our previous results:

The term on the right side is substituted for 1+2+3+4+...+n, as we have already proven the statement right:

Using the same denominator and adding the fractures, we can see that the last step equals (n+1)*(n+1)+1). This is the same as (n+1)*(n+2). This is exactly what we wanted to prove. A true equation tells us, the formula is right and can be used to calculate the sum of every natural number for any natural number we put into it.

We have shown that our formula is true for =1, =n and =n+1. After we have completed these steps, the process of induction is finished, because we prove the term right for every sum we want to calculate.

Thanks for reading :)

Sources

Text

https://www.ck12.org/book/CK-12-Math-Analysis/section/7.3/

http://mathcentral.uregina.ca/qq/database/qq.02.06/jo1.html

http://www.math.kit.edu/iana2/~mandel/seite/schnupperkurs/media/induktion.pdf (translated)

https://www.arndt-bruenner.de/mathe/Allgemein/summenformel1.htm (translated)

http://www.math.uni-bremen.de/didaktik/ma/ralbers/Veranstaltungen/MaDenken1112/Material/SkriptWiSe_K2.pdf (translated)

https://de.wikipedia.org/wiki/Gaußsche_Summenformel (translated)

https://en.wikipedia.org/wiki/Mathematical_induction

Pictures

https://upload.wikimedia.org/wikipedia/commons/thumb/c/cb/Gau%C3%9Fsche_Summenformel_geometrisch.svg/1280px-Gau%C3%9Fsche_Summenformel_geometrisch.svg.png

All equations were made with Microsoft Word and were published on my imgur account

https://i.imgur.com/vXRlhuM.png?1

https://i.imgur.com/5wEqmnP.png?1

https://i.imgur.com/2Orckh7.png?1

https://i.imgur.com/DcqdmZz.png?1

https://i.imgur.com/WFjbpDt.png?1

https://i.imgur.com/uaG7UIn.png?1

Comments

[statistician]

You can even simply the thought behind this further by simply taking number 1 to n and listing each number in succession and then below each number list n to 1 (backwards). Then summing down the row. You'll notice that each number summed down is simply n+1. But because we've counted each column of numbers twice, we need to divide by 2 to "normalize" the results and get the correct answer. So for example take n = 4. Then write out:

1 2 3 4
4 3 2 1

And now add from the 4 columns:

1 2 3 4
4 3 2 1

---

5 5 5 5

Summing this is 5+5+5+5 or [5 x 4 or 5 x (n-1)] = 20. Since we've double counted each column, we need to normalize by dividing by 2, which results in 20/2 = 10.

Notice that 1 + 2 + 3 + 4 = 10.

[aximot]

Nice and simple explanation thanks for that :)

[statistician]

Yes, this is just like the method you initially mentioned, but without the geometry explanation. Nice post! Similar induction arguments can be made to obtain simple formulas for the sum of numbers squared, cubed, etc. There is a nice body of work around these methods.