In school level physics, the famous Newton's laws of motion came out of nowhere. We took those laws for granted and we used it to solve different mechanics problems. But you may have wondered where do these equations come from? Why do we need to make these equations valid even using constraint forces like a normal reaction, tension etc. though seems not intuitive? Does it have deeper fundamental meaning? Or at least how can this law be proven?. In this article, I will write about a deeper fundamental principle called the principle of least action in which both classical and quantum mechanical equations of motion are based on and will derive Euler Lagrange equation using this principle.
The principle of Least Action:
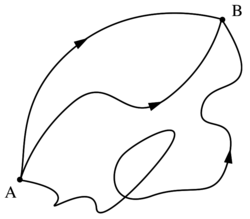
Consider a particle which is at point cell A at time t1 and it moves to point B at time t2. This can happen in many ways. It can follow paths 1,2,3 or any other paths as shown in the figure. But, the principle of least action tells that the particle follows the path in which the action is the least. So, you may wonder what is this action? At first, let's consider a function L which is the function of position and velocity. Why function of position and velocity? In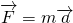 
, the acceleration is dependent on the force. So, we take the idea that the position and velocity are independent. For simplicity, I will consider single particle and one-dimensional coordinate system.
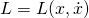
Then, Action is the sum of this function at different times. So, since the path is continuous.
Action(A) = 
This value of action differs from path to path. The path followed by the body is such that the value of Action is least.
=0
From experience, it is known that for the conservative mechanical system, the value of 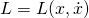is the difference between the kinetic and potential energy of the system.
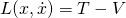
T is kinetic energy and V is potential energy of the particle.
= 
Euler Lagrange Equation:
Actually, the function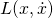 
is called Lagrangian. Since the t1 and t2 can be anywhere, the differential equation can be obtained from the least action principle.
A =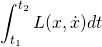 
The endpoints A and B don't change with time. So, taking differential under integral.
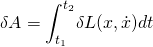
Using multivariable calculus; the calculus of variation;
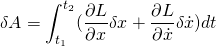
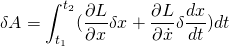
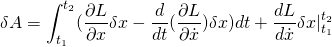
The endpoints are fixed so the last term integrated from t1 to is 0.
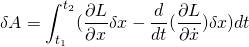
This is true for an arbitrary dx so,
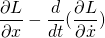= 0
This differential equation is for the single particle system in single coordinate. For general differential equation.
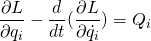
Example:
Consider a simple pendulum. The mass of the bob is 'm' and length of the string is 'l'. Let at any instant, it is making an angle of \theta with the vertical.
.png)
L= T - V
= 
= 
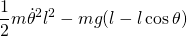
so,
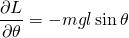
and,
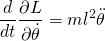
Using Euler Lagrange equation;
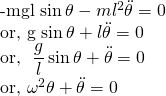
This doesn't look like the equation of motion. This is actually differential equation which should be solved to get an equation of motion in a usual form. This problem can also be solved using Newton's law. This solution is in coherence with the solution using Newton's law. So, the Lagrangian we took earlier is correct. Now, we can extend this process to find the equation of motion of the double pendulum or let's say triple pendulum. It is very difficult to find an equation of motion of these systems using Newtons laws. Euler Lagrange method seems tedious for simple problems but its really useful for the complicated problems. In the example above, the motion was known without the knowledge of constraint force i.e. Tension. The equation is in a generalised form which is convenient to solve problems consisting of many coordinates(degree of freedom). Not only this, this equation is equally important in other parts of classical mechanics. We can say that Euler Lagrange equation of mechanics is equivalent to Maxwell equations of classical electrodynamics.
References:
Images:
1.wikipedia.org/wiki/path_integral_formation
- www.aoengr.com
Post:
- Goldsteins Classical Mechanics
- https://ocw.mit.edu/courses/physics/8-01sc-classical-mechanics-fall-2016/
- https://onlinecourses.nptel.ac.in/noc17_ph07/preview
@bikkichhantyal Wow, Nice post. I Just loved to see your post. I have also recently posted some stuffs, have a look at my blog post.
Thank you!!
Ok I will check it out.
Congratulations @bikkichhantyal! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPThis is the topic we doing now but we are in dubois reymond related topic
I didnt understand. Pardon me?
amazingg post!!! :D
Thank you so much :D
This post has received a 5.29% upvote from @msp-bidbot thanks to: @bikkichhantyal. Delegate SP to this public bot and get paid daily: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP Don't delegate so much that you have less than 50SP left on your account.
You got a 5.88% upvote from @brupvoter courtesy of @bikkichhantyal!
You got a 1.47% upvote from @getboost courtesy of @bikkichhantyal!
You got a 0.91% upvote from @allaz courtesy of @bikkichhantyal!
You got a 12.50% upvote as a Recovery Shot from @isotonic, currently working as a funding tool, courtesy of @bikkichhantyal!
@isotonic is the Bid Bot of the @runningproject community.
Earnings obtained by this bot, after paying to the delegators, are fully used to increase the SP of the @runningproject from which all affiliated members are benefited.
Check @runningproject posts in order to know further about.
@masterbot has been called by @bikkichhantyal to give you 26.74% upvote!
Check this post for information about delegation. Make me strong!
You got a 3.85% upvote from @mercurybot courtesy of @bikkichhantyal!
This post has received a 7.27% upvote from @lovejuice thanks to @bikkichhantyal. They love you, so does Aggroed. Please be sure to vote for Witnesses at https://steemit.com/~witnesses.
You got a 0.76% upvote from @postpromoter courtesy of @bikkichhantyal!
Want to promote your posts too? Check out the Steem Bot Tracker website for more info. If you would like to support the development of @postpromoter and the bot tracker please vote for @yabapmatt for witness!
This post has received a 2.73% upvote from @aksdwi thanks to: @bikkichhantyal.