Motivation
Nature is dynamical. All the things are changing due to other things. The relation can be precisely expressed in terms of mathematics. It is called mathematical modelling. In doing so, many physical problems lead to differential equations. So, in this article, I will give a gentle introduction to the differential equation.
Think about this problem: If the velocity of body v(t) is given by; v(t) = t/5 . How does the position of body s(t) relates to the time? If you don't know this, then don't worry. You would be able to do it after studying this article. Here are some practical problems which will motivate you:
Example 1:
Consider a simple physical phenomenon in which a body is falling under the action of gravity. Let's neglect air resistance to make it simpler. Then, Only considerable force is gravity which is equal to weight.
F= W
F= mg
According to Newtons law, F= ma
ma = mg
a= g
We know that acceleration is constant.
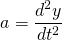
so, 
= g
It is a differential equation. Solving this differential equation, the position of the body at later time t can be known.
Example 2:
Consider another problem. A body at temperature T is cooling in the atmosphere of temperature 
.
According to Newton’s law of cooling, "The rate of cooling of the body is directly proportional to the temperature difference between body and surrounding."
Let,
T = temperature
t = time
k = proportionality constant
Then, according to law;
It is a differential equation. This equation can be solved to get the relation between temperature and time. The temperature of the body at later time t can be known.
Example 3
(https://physics.stackexchange.com/questions/133091/the-acceleration-vector-of-a-simple-pendulum)
Consider a simple pendulum as shown in figure, Then, mgsinθ = ma
g sin θ = a
from figure,
sin θ =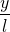 
we know, a =
So,
g() =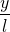
It is a differential equation. If we solve it, we can get a relation between displacement(y) at any time(t). Actually, y= r sin(wt) is obtained.
These are few examples of the application of differential equation.
It is also used in
i) Electrical engineering to obtain the relation between voltage and current with time.
ii) In mechanical engineering to obtain the equation for deflection of beams, heat conduction etc.
iii) In radioactivity, relates activity with the number of atoms remained.
iv) In the modelling of population growth, bacteria growth, predicting doubling time etc.
v) Deriving equations of motions, solving mechanics problems etc.
vi) Chemistry, chemical kinetics. etc.
There are many application of differential equation in physics, chemistry, engineering economics etc. So, it's very important for us to study differential equation and hence solve it.
History
The history of differential equation dates back to Newton-Leibniz year when calculus was invented. i. In around 1671, Sir Isaac Newton classified differential equations into three classes.
class 1:
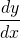= f(y)
Class 2:
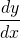= f(x,y)
Class 3:
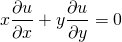
Classes 1 and 2 contain ordinary derivatives and are called ordinary differential equation.
Class 3 contains partial derivative term and equation is called partial differential equation.
ii. In around 1675 Gottfried Leibniz wrote the following:
Then, the study of the differential equation is said to have begun.
iii. In around 1675, Newton first solved the differential equation using infinite series.
iv. In 1692, the method to solve homogeneous differential equation was known to Bernoulli.
v. In 1691, Leibniz found out the method of separation of variables.
It wasn’t able to solve differential equation: x dy −ydx = 0 since it would lead to
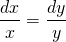
Logarithm wasn't known then. John Napier studied on Logarithms and its solution was made possible.
vi. in 1695, James Bernoulli proposed Bernoulli equation.
It is in the form:
vii. Leonard Euler found the way to reduce the second order differential equation to first and to find the solution using known solution. It also includes integrating factor.
viii. Alexis Clairaut used the method of differential to find particular solution of the differential equation of the form:
It is known as the clairaut equation.
ix. Lagrange work on determining the integrating factor for the general linear differential equation and in this process formalized the concept of the adjoint equation.
x. Later, the focus was given to special functions which are Bessel, Legendre, Hermite etc.
Introduction
The equation containing derivatives or differential term is called differential equation. eg.
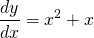
If the differential is ordinary then the equation is called ordinary differential equation.
eg.
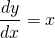
If the differential is partial then the equation is called partial differential equation. eg.
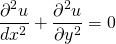
Order of the Differential Equation
The highest number of times the derivative on the term of the equation is called order of that differential equation.
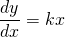
It is first order differential equation.
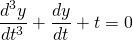
It is third order differential equation.
Degree of the Differential Equation
The power raised to the highest order differentiated term in a differential equation is called the degree of that differential equation.
eg.
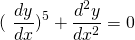
It is the first degree differential equation.
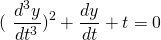
It is the second degree differential equation.
Solution of Differential Equation
The relation between the independent and dependent variable which doesn't contain the differential term is called solution of the differential equation.
In the differential equation:
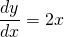
The relation between dependent variable y and independent variable x is the solution.
From the knowledge of derivative,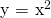 
is the solution because
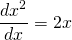
which satisfies the differential equation.
Also,putting
It also satisfies the equation.
In general, 
satisfies the differential equation. Here c is arbitrary constant.
It is called general solution. It gives the family of curves.
If the condition is given i.e. the curve passes through (1,1) ;
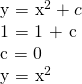
It is the particular solution. To know where a function y = f(x) is the solution of the differential equation or not, we put y= f(x) in the differential equation. If it satisfies equation, its the solution and if it doesn’t, it isn't the solution.
References
Thomas Calculus, Thomas and Finny
Advanced Engineering Mathematics, Erwin Kreyszig
A first course in differential equations, Dennis G Gill
This post has received a 4.33 % upvote from @aksdwi thanks to: @bikkichhantyal.
You got a 0.64% upvote from @postpromoter courtesy of @bikkichhantyal!
Want to promote your posts too? Check out the Steem Bot Tracker website for more info. If you would like to support the development of @postpromoter and the bot tracker please vote for @yabapmatt for witness!