Introduction
Triangle in a plane has three linear elements and three angular elements. Three linear elements are three sides and three angular elements are three angles of the triangle. When any three elements are given, we can find remaining three elements, this is called solution of the triangle.
Different cases under which triangle can be solved are as follows:
i) Three sides given (SSS)
ii) Three angles given or Two angles given (AAA)
iii) Two sides and included one angle given (SAS)
iv) A side, the angle opposite to it and an angle adjacent to it (AAS)
v) Two sides and angle not included is given (SSA)
vi) A side and the two angles adjacent to it (ASA)
In case (ii), when three angles of the triangle are given, we can find the infinite number of such triangles. These triangles are called similar triangles.
Relevant theorems
Consider a triangle with side a, b, c and corresponding angle A, B, C.
The theorems which are needed to solve triangle are described below.
i) Angle rule:
The sum of the angles of triangle is 180 
In triangle above,

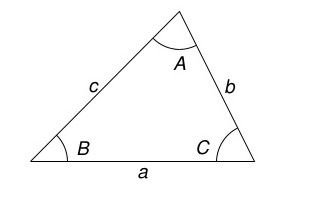
ii) Law of sine:
If A, B, C are three angles of triangle and a, b, c be three sides then,

iii) Law of Cosine:
If A, B, C are three angles of triangle and a,b,c be three sides then,

Case I: Three sides given (SSS)
Here, a, b, c are known. Then,
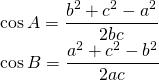
then,
We can find all the angles.
Example 1:
The sides of the triangle are 3, 4, 5 cm. Solve this triangle.
Solution:
Let a= 3 cm, b = 4 cm and c= 5cm. A,B,C be corresponding angles. Then,
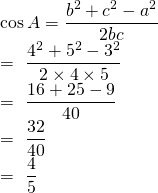
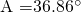
so,
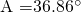
Again;

so,

Further,

Case II: Three angles are given
That means A, B, C are known.
From sine law;

It doesn’t have a unique solution. We can find an infinite solution. These solved triangles are called similar triangles.
If two angles are given, we can find the third angle using
 and sine law can be used.
and sine law can be used.
Example 2:
If three angles of a triangle are 30◦, 60◦ and 90◦, solve this triangle.
Solution:
Using Sine law:

So,
a = 2k
b = 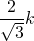
c = k
It is the solution. k is a constant number.
When k = 1;
a = 2 cm , b =  cm, c = 1 cm is one solution.
cm, c = 1 cm is one solution.
Case III: Two sides and included angle given:
That means, sides a, b and angle C are given
From cosine law;
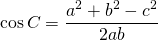
value of c can be calculated.
From sines law;

From this, the value of A can be calculated.
Also, 
From this, the value of B can be calculated.
Example 3
If a = 1, b = 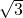
and C =  , Find remaining angles and sides.
, Find remaining angles and sides.
Solution:
From cosine law;
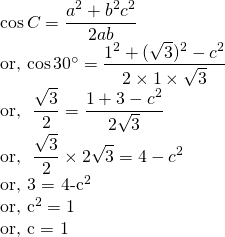
From sines law;
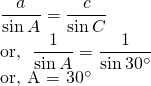
also,
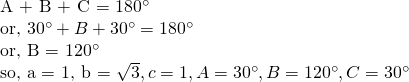
Case IV: A side, the angle opposite to it and an angle adjacent to it (AAS)
That means a, A, B is given;
From,  , C can be calculated.
, C can be calculated.
From sine law;

From a 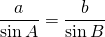 , b can be calculated.
, b can be calculated.
From  , c can be calculated.
, c can be calculated.
Example 4:
If A = 60◦,B = 75◦ and a = 2√3, solve the triangle.
solution:
we know;

From sine law;

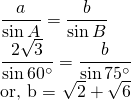
Again;
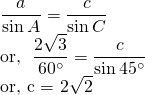
Case V: Two sides and angle not included is given (SSA)
That means sides a,b are given and the angle A or B is given( Consider A)
Then,
From sine law;

a, b, A are given so we can calculate, B from first two relations. ie.

Then, from  , C can be calculated.
, C can be calculated.
From 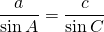
c can be calculated.
Example 5:
Given a = 3, b = 3 , A =
, A =  , solve the triangle.
, solve the triangle.
From sine law;

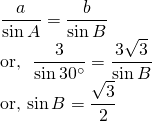
These take two solutions, B =  . Since it has more than one solution, it is called the ambiguous case.
. Since it has more than one solution, it is called the ambiguous case.
When B = 
or, c = 6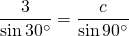
When B = 120
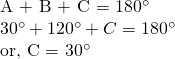
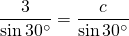
or, c = 3
Case VI: A side and the two angles adjacent to it (ASA)
That means a, B, C are given;
From  , A can be calculated.
, A can be calculated.
From sine law;
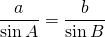
b can be calculated.
Again from sine law;

c can be calculated.
Example 6:
If  , Solve the triangle.
, Solve the triangle.
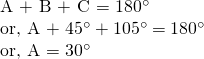
From sine law;
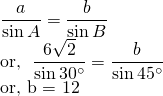
Again,
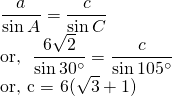
References
Basic Mathematics; DR Bajracharya
Algebra and Trigonometry; Ron Larson
Essential Trigonometry; Tim Hill.
Khan academy video lectures
quicklatex.com for the maths code
Release the Kraken! You got a 0.96% upvote from @seakraken courtesy of @bikkichhantyal!
Geometry is an really unusual, unseen topic on Steemit. Thanks for sharing!
Yeah.
Actually, there are few very posts about mathematics. I will be posting mostly related to it.
You got a 3.35% upvote from @mercurybot courtesy of @bikkichhantyal!