
In a previous post I detailed the kinds of calculations necessary for calculating accurate artillery fire in Arma 3 (using ACE for extra realism). While it's great to get a general estimate of how to aim using precise formulas, what if there are lots of unknowns that can affect the performance of the calculations? In the last post I mentioned--but did not correct for--air resistance. This single component significantly affects the usefulness of the model in my last post, not to mention wind and air temperature.
In this post I will use a few machine learning techniques implemented in Python to train a model capable of accurate artillery fire, without fancy physics formulas or rough estimates in the vanilla Arma 3 game, and a future post may describe this approach with mods such as ACE.
Collecting the Data
Before I could begin training a model for use in machine learning, I first had to collect data that could be interpreted by a learning algorithm. To that end I had to fire up Arma 3 and manually enter in my (eight-figure) coordinates, elevation, and the corresponding information about each target position.
I tried to get a varied group of target positions, so that our learning algorithms would be able to find the relationships between things such as distance and elevation. Once I selected a position to record, I also recorded what the in-game firing computer reported as the correct angle to aim at. This way we can use the results from the computer to train our model. In total I collected data from 29 target positions, which mind you, is not very many for most applications of machine learning.
I collected data from 7 different grids, four points from each grid, and used the "close" setting on the M4's firing computer.
For this run I played without the use of any mods that would affect the ballistics of shells in the game. I first wanted to get a sense of how to collect data, which data would be most useful, and how to transform it into a learner before I increased the complexity required to accurately aim shots.
The data corresponds to information from the M4 "Scorcher" NATO artillery platform in Arma 3. If you would like to peruse the data yourself, you can view it here.
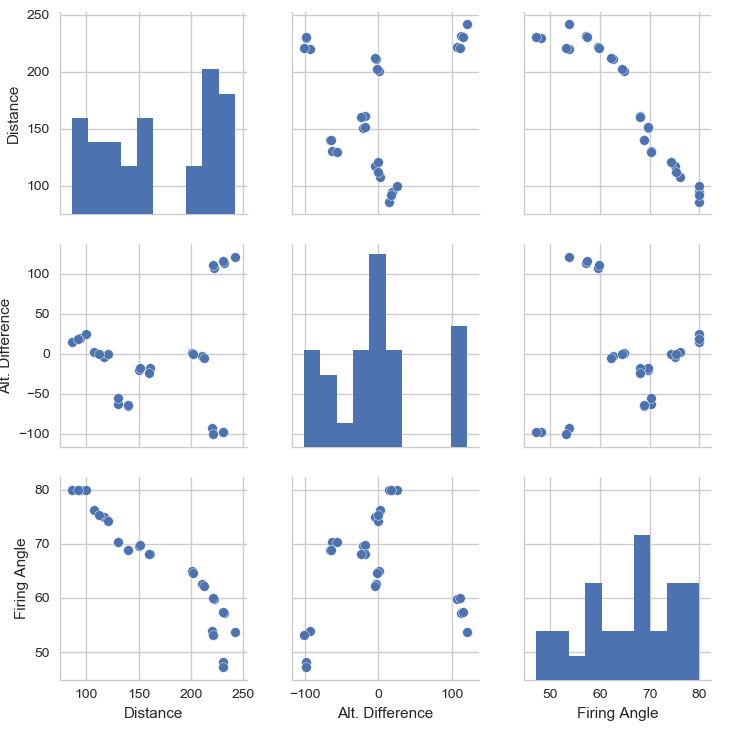
For the sake of visualization and gaining some intuition of our dataset, I decided it would be best to create a plot of three different components, the distance, elevation difference, and reported firing angle from the firing computer. This will allow us to see if any clear patterns are present.
As expected, it seems there is a clear relationship between distance and firing angle, however the relationship between elevation difference and firing angle is less clear.
Selecting Approaches for Machine Learning
There are many different machine learning algorithms one could use for this particular task, some more suited than others. The first thing I wanted was to select an algorithm suited for regression. In other words I need an algorithm that is just as capable of producing a result like 54.72° as 63.99°.
Regression algorithms work by attempting to fit a line, curve, plane, or hyperplane to the data while minimizing a cost function. The cost function can vary, but a popular cost function is the mean-squared error, which looks something like this:
We can use the cost function to help judge whether or not one model is better than another.
Random Forests and Decision Trees
Since I wasn't sure which factors were affecting the calculations needed for predicting the firing angle, my first thought was to use an ensemble of decision trees known as a random forest.

Not that kind of forest!
Decision trees are a simple idea, you have some choice, and you map out the possible outcomes for the choice. Repeat until you have covered all the choices and their resulting choices and you get something that vaguely resembles a "tree" of decisions (hence the name). If you are curious about more detail about how decision trees work, let me know in the comments and I'll consider making a post detailing their strengths and weaknesses. But for our purposes it is enough to know that decision trees can handle all kinds of weird cases and don't require us to modify our input data.
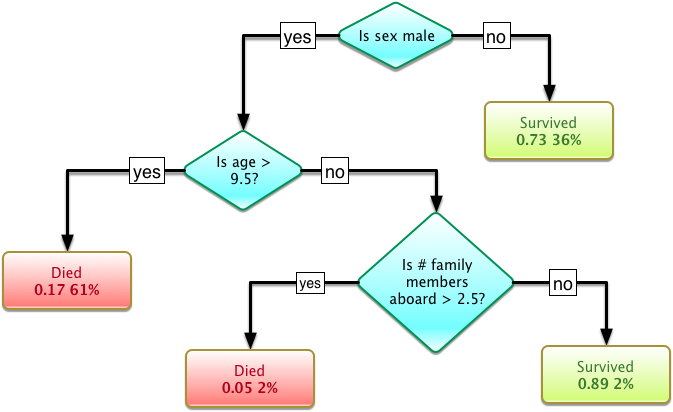
Wikipedia's rather morbid example of a decision tree of predicting whether or not a given passenger survived the Titanic.
If you combine a bunch of slightly different decision trees together, you can create a "random forest", where the final outcome depends on either a majority of the trees "voting" for a particular choice, or an average of all the reported choices.
Polynomial Feature Fitting
Despite random forests' ability to handle extremely complex cases, this can also mean that for sparse datasets on simple problems it can be prone to overfit the training data. Given that we have some reliable intuition that the shell will follow a ballistic trajectory, I decided that it would also be worth training a much simpler model to attempt to fit the data.
Another type of regressor is known as a polynomial regressor. Polynomial regressors work by fitting a line or plane to a dataset that minimizes its cost function. They create an equation which can be modified in degree to fit the presented data. The polynomial takes the form:
The degree of the polynomial defines how many terms it will have.
Polynomial regression can work well when our data is continuous and doesn't have abrupt jumps or changes and follow a more simple relationship. More complex data can also be fit with higher-degree polynomials, but we have to be careful as high-degree polynomials can really overfit the training data and fail to generalize to new situations.
Training Machine Learning Models for Aiming Artillery
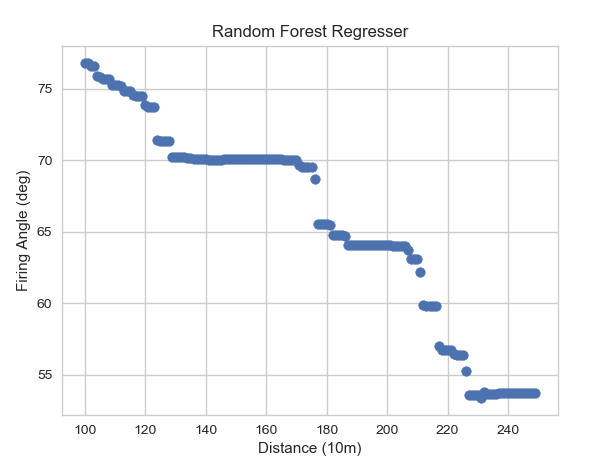
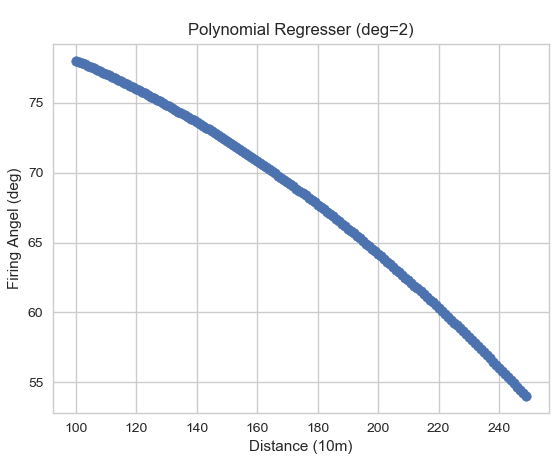
From our earlier visualization of the data, it seems that the most important features are the distance and elevation difference of the firing position and target. I trained two models, a random forest of 1000 small decision trees, and a two degree polynomial function and plotted their predictions for easy comparison. The figures below pit the models against each other assuming no elevation difference (data can be hard to visualize with more than 2 variables).
The random forest had an MSE of about .963 and an R2 score of 98% on test data.
The polynomial model had an MSE of about 1.466 and an R2 score of 97% on test data.
As you can see from the charts above, it is always important to visualize the data when possible. Though the random forest scores better in our cost function, it clearly does not seem like it would generalize well in situations outside its training set.
Putting the Models to the Test
After training the two models, I decided to put the models to the test in game and compare them against each other. And what better way to test the two models than to have them shoot at each other, and the model to inflict the most damage after 10 shots wins!
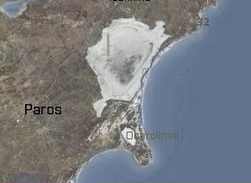
I chose the dried lake east of Paros as the location for the duel. The platforms were located at grid 23701880 and 23201730.
Each artillery piece was surrounded by 6-8 men, standing in formation around the piece.
An interesting fact about this test is that the distance between the platforms falls in the "gap" from our data, meaning that neither model has a reliable data point near this distance (about 1.7km). This allows us to get more insight into how well each model is at predicting the firing angle when it matters.
I can't say I would have wanted to be any of those brave men.
Results
After firing 10 rounds from each platform, it was quite obvious which model was better when pitted against the other. Each dot in the images below represents where a shell landed.

The results from team forest. You can see that it undershot the target by about 100m. The dots on target came from shots using the in-game artillery computer.
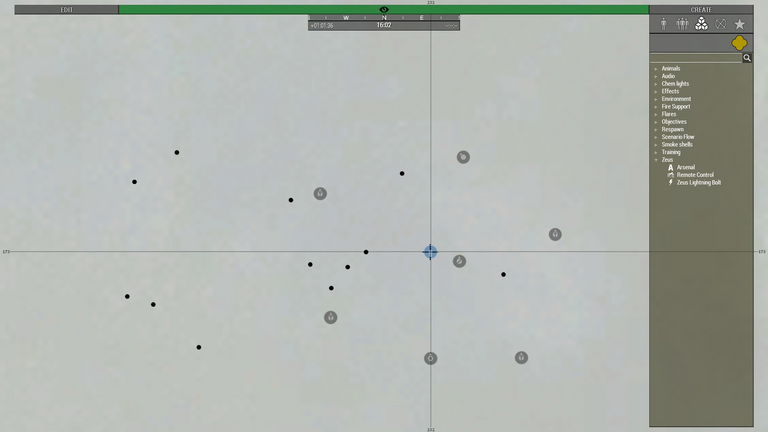
The results from team polynomial. For reasons unknown, shots seemed to land west of the target by about 10-20m, but the shots were much closer than team forest. The closest three dots came from the in-game artillery computer.
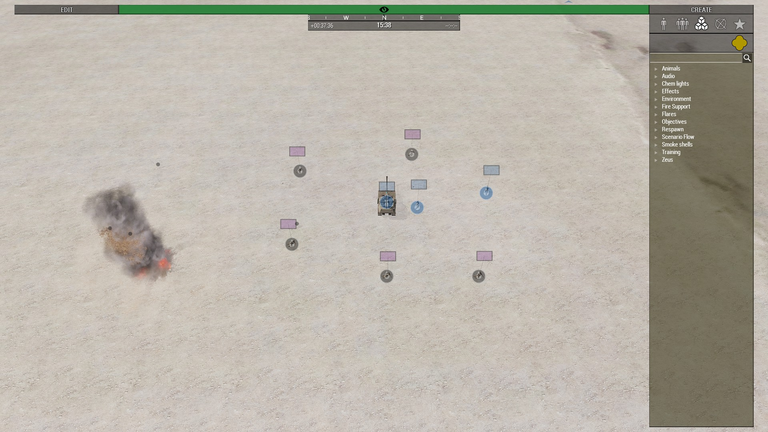
A single hit from team polynomial killed nearly all men standing around team forest.
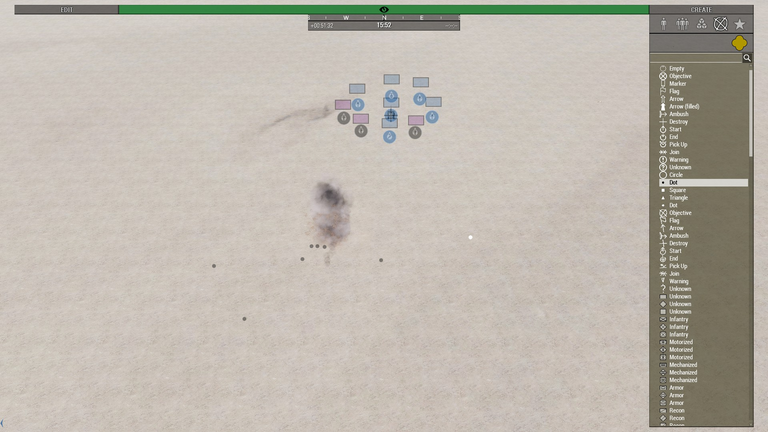
Despite undershooting, one shot from team forest managed to kill 3 men on team polynomial.
Conclusion
As expected, the polynomial model significantly outperformed the random forest model on even terrain at close distances. It remains to be seen how the random forest model would perform given a significant elevation difference, but this test suggests that the random forest does not seem like a good model for general use.
Future Plans
For a future post I plan to test these models against more varied conditions and collect more training data. Then I hope to introduce elements from the realistic ballistics calculations in ACE to train a model capable of accurately aiming even in windy conditions.
Let me know in the comments below what you would like to see and I may cover it in a future post!
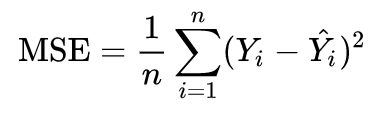
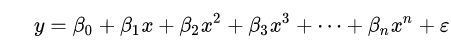
Your post was mentioned in the Steemit Hit Parade for newcomers in the following category:Congratulations @chosunone!
I also upvoted your post to increase its reward
If you like my work to promote newcomers and give them more visibility on Steemit, feel free to vote for my witness! You can do it here or use SteemConnect
I want to go to the trending page of Steemit and see content of this quality on diverse topics. But that is not obtainable right now. I don't know much about the subject, but boy am I impressed! Because I think this post deserves a lot more visibility, I just resteemed it to my 1k1 followers. And I added my 20 cent upvote. I hope that does anything ;-)
Just steem on.
Thanks a lot! I too want to see higher quality content and I'm honored to be considered quality.