Hi friends. So @dexterdev is back with another cool topic. Let us begin! I will start with a picture of a beautiful fish named Emperor Angelfish (Pomacanthus imperator). What interests me in this fish is its patterns. So beautiful right? The interesting part is that scientists have modeled these patterns mathematically!
 FIGURE 1 Image Source: Flickr, Uploader: Cliff, License: CC BY 2.0
FIGURE 1 Image Source: Flickr, Uploader: Cliff, License: CC BY 2.0Inspiration for this post
So last weekend I was visiting my hometown in Kerala. I was walking through the local fish market and saw some tuna (കുടുത pronounced ku-du-tha in Malayalam). Some snapshots below:


Do you see some patterns on these fish-skins? Something immediately struck my mind! Something which I have learned in past in my systems-biology classes. We were taught reaction-diffusion systems and about pattern formation etc in those classes. I have simulated patterns like this. You can see it here:
The above simulations are something called Gray-Scott reaction-diffusion model. I have written some articles in past about the reaction-diffusion systems. You may want to see those (The first link has a Matlab code to generate these patterns):
- An example of Reaction-diffusion process involving 2 species (Gray-Scott model).
- Explaining Reaction-Diffusion process (continued)
I agree that the patterns in the video are not exactly like the patterns on fish. But you can get very strikingly similar patterns with different parameters. You can explore the parameter space in this webpage. You just click a region of pattern, corresponding simulation can be visualized from youtube.
What did researchers modeled?
The history of Reaction-diffusion model traces back to the final paper by Alan Turing. Yes!

The great Alan Turing conceived the concept of reaction-diffusion. Was he interested in biology? Yes! The title of his last paper says it all. The Chemical Basis of Morphogenesis was an attempt to model a very complex biological process namely morphogenesis! Morphogenesis as per wikipedia goes like this:
Morphogenesis (from the Greek morphê shape and genesis creation, literally, "beginning of the shape") is the biological process that causes an organism to develop its shape. It is one of three fundamental aspects of developmental biology along with the control of cell growth and cellular differentiation, unified in evolutionary developmental biology (evo-devo).
So it is about how an organism attains its shape and patterns etc. His model was purely mathematical. Using two simple concepts like diffusion and reaction, he modeled a complicated process in a very minimal way. The idea basically was to model a PDE (partial differential equation) model which encompasses a chemical reaction term and particle diffusion term. The hypothetical particles were called morphogens for obvious reasons. Morphogens may be practically protein molecules etc. And the counterintuitive result was that diffusion which usually is a stabilizing process, in presence of reactions (with appropriate parameters of course) give rise to instabilities in the system which show up as oscillations in space and time.
The model is great! But the million dollar question is now Is there any real-life examples? So recently from Japan, Kondo et al (see references) came up with some real examples. Examples in the form of patterns in Emperor Angelfish (Pomacanthus imperator). See FIGURE 1.
The Kondo model
The Kondo model in equations is as below:
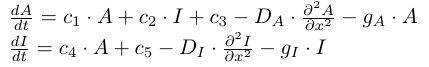
The second derivatives terms are diffusion terms. Diffusion is a simple concept and you may look up its wiki page here. Now coming to the reaction terms the subtracted terms are decaying chemicals and added (positive) terms are the addition of chemicals etc. And the single derivative terms, the rate of change with time is the sum of both reaction and diffusion terms.'A' and 'I' are the hypothetical activator and inhibitor molecules. 'x' is the one-dimensional space and 't' is the time. c1,c2,c3 etc are reaction rates. DA and DI are diffusion coefficients, the rate at which the reagents diffuse through space. For specific parameter values, the system mimics the pattern evolution on this particular fish very accurately! The concentration of 'A' molecule in space with time gives the evolution of pattern. Here is an approximate illustration based on the Kondo's paper:
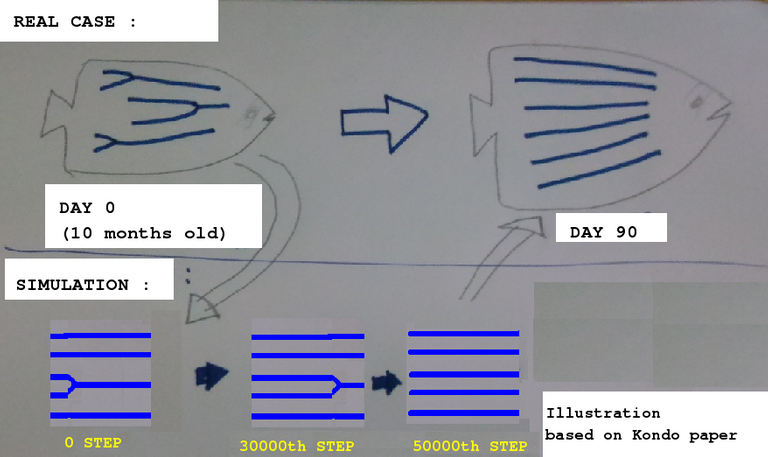
I think this is a very interesting aspect of mathematical modeling. I guess you enjoyed this article. I have attached links to relevant papers in the reference. By the way, there are multiple examples like this. But only in certain cases, we really get to know the real molecules in action. In most hypothetical-molecule models, the model is a dimensionally reduced representation of a complicated system with many participants but still reproduces the results very nicely.
My plan for future
I will once explain how to understand reaction-diffusion systems more nicely. Maybe in my Visually explained! series.
References
[1]: Turing, Alan Mathison. "The chemical basis of morphogenesis." Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences 237.641 (1952): 37-72.
[2]: Kondo, S. and Asai, R. (1995) A reaction-diffusion wave on the skin of marine angelfish Pomacanthus. Nature 376, 765–768
[3]: Watanabe, Masakatsu, and Shigeru Kondo. "Is pigment patterning in fish skin determined by the Turing mechanism?." Trends in Genetics 31.2 (2015): 88-96.
If you like my content please upvote and resteem it. Below are few of my recent posts, you may find interesting:
- Phospholipids: The unsung heroes in biomolecules!
- Information-driven processes versus Self-Organization processes in Biology
Join #steemSTEM
Join the active science community #steemSTEM at discord: https://discord.gg/BZXkmWw
And to steemSTEM Beginners: You can ask for help in our discord page. There are people ready to help you there.

All images without image sources are my creations :)
Follow me @dexterdev
____ _______ ______ _________ ____ ______
/ _ / __\ \//__ __/ __/ __/ _ / __/ \ |\
| | \| \ \ / / \ | \ | \/| | \| \ | | //
| |_/| /_ / \ | | | /_| | |_/| /_| \//
\____\____/__/\\ \_/ \____\_/\_\____\____\__/
Wouldn't think of mathematics to describe fish patterns, but then again, I'm not a world renown mathematician like Turning.
Great post and a very interesting subject @dexterdev!
I will be looking forward for your Visual Explained post about it too :)
I will surely do it once. The thing is the math is quite challenging. So for a wider audience, I have to come up with some easy and intuitive explanation. Let me think about how to make this concept more presentable. @katerinaramm : thank you for reading this.
Content type: Long, (mostly) popular




Awarded 4 out of 6 owls:
Great job!
Details: The spelling and grammar was not awarded since it contains a number of grammatical errors. No spelling errors were found. The clarity and completeness owl was almost awarded. It should be mentioned that in the case of the Zebra fish there is molecular evidence which indicates that the pigment patterning is determined by the Turing mechanism. In addition the mechanism discovered is different from what the mathematical model predicted Watanabe,2015
Amazing post! It's great how math and computational skills can be really useful in biology.
Thank you. Yeah math and computational skills can be really useful in biology. Especially these days biology is looking towards more quantitative style of problem solving. More engineers, More physicists and More computer scientists are starting to look into biology. This is an exciting time period.
Interesting one @dexterdev
Well, I only know about the developmental biology of an organism, how it attains its shape and development of organs. I didn't know that it can can be related mathematically....
Cheers
Good to know that you found it interesting. There are multiple examples. In my previous examples, I have more reaction-diffusion related articles. Even the chemical system Beluosov-Zabotinsky reactions are biologically inspired ones. Similarly, minD system which dictates the E. Coli bacterial division is also modelled via reaction-diffusion. But again there are a lot of criticisms too. Mainly from pure biologists.
I guess if you keep thinking mathematically, everything in nature can take a mathematical form. This is truly amazing. Some of us are not very good with math so than you for taking the pains to spare us that :)
I happy to hear that this helped. :) In fact, the math in notations may be difficult. But if we spare some time with the concepts they are not very hard to crack. :)
Good to see this paper of Turing's cited!
Many CS people don't know his contribution in this field. It is literally non-equilibrium statistical mechanics.
Very interesting article. It's also nice to see MATLAB used here. Sure brings back memories.
Following you now.
Do you use MATLAB. Matlab ruined me. :P It made me lazy. haha. I should have spent more time on python instead. But when I was beginning these things in 2006 or so I never knew about python. Later numpy gained popularity. :(
@mathowl
Congratulations @dexterdev! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPBeing A SteemStem Member
That was a great and quite informative post @dexterdev. Please keep up the quality posts. I will stay tuned in order to find out more about the different sorts of models used to classify fish.
Thanks
Thank you for the encouragement. :)
Hey, nice post! I like your content. Keep up the good work! It's always nice to see good content here on Steemit! Congratulations :)
Thank you. 😃