La enseñanza de la historia de la matemática enfrenta dos problemas fundamentales. El primero de ellos es el desinterés de los propios matemáticos por aprenderla. En su empeño de construir un edificio lógico sin fisuras, los conceptos nuevos superan a los viejos hasta el punto de eclipsarlos o desparecerlos por completo. La otra dificultad está relacionada con la anterior de formas muy sutiles: se refiere a la transmisión de la historia a través de medias verdades, lo que suele ser peor que la transmisión de mentiras. Como ejemplo de esto último, podemos mencionar que muchas veces hemos oído que los pitagóricos descubrieron la irracionalidad de la raíz cuadrada de 2, y la demostraron tal como la enseñamos hoy a los adolescentes: con la aritmética elemental.
En algún momento hablaré de este tema específico, pero lo que me interesa recalcar en este post es que los griegos no tenían ningún concepto de número racional y mucho menos irracional. Su concepto de número solo abarcaba lo que conocemos como número natural, con la deficiencia adicional de dejar por fuera al 1, al que no consideraban un número. Es decir, número para los griegos era lo que nosotros hoy sabemos incluído en el conjunto
No obstante, los griegos nos dieron el área de varias figuras planas importantes y el volumen de algunos sólidos notables. Pero para el matemático actual, las palabras área y volumen están indisolublemente ligadas al concepto de número real. Es más, los libros de geometría moderna definen el área como una función del conjunto de las figuras planas sobre el conjunto de los números reales no negativos, y el volumen de una manera similar en el espacio. ¿Cómo congeniamos entonces una cosa con la otra? Es decir, ¿cómo calza la verdad histórica con nuestra práctica actual?
Empecemos por los racionales. En los dos posts anteriores (primero y segundo) hablábamos de la fe inicial de los pitagóricos en la conmensurabilidad absoluta; esto es: dadas dos magnitudes A y B cualesquiera (podemos pensar en segmentos para simplificar) siempre encontraremos una magnitud menor a ambas que quepa también en ambas un número entero de veces. Si esta magnitud más pequeña cabía (por decir algo) 7 veces en la mayor A y 5 en la menor B, entonces se afirmaba que A es a B como 7 es a 5, frase que la posteridad abrevió con la siguiente notación
Si se observa bien, lo que hay allí es un proceso de comparación no uno de aritmetización. La frase dice que A está con B en la misma relación que 7 está con 5. Fue después del proceso de unificación cartesiana que pudimos escribir
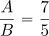
para que la razón 7:5 se convirtiera por fin en el número 7/5.
Comentemos ahora los irracionales. La esperanza en la conmensurabilidad absoluta se rompió con el cuadrado y el pentágono regular y los pitagóricos no pudieron definir las razones si no terminaban en razón de números, problema que resolvió Eudoxo algún tiempo después. Eso permitió luego a Euclides decir cosas como su proposición XII.2: Los círculos están entre sí como los cuadrados de sus diámetros, sin preocuparse de que las razones involucradas en esa afirmación pudieran expresarse mediante números. No podemos entrar por ahora en el análisis de la teoría eudoxiana, pero una analogía nos ayuda a entender la afirmación anterior sin usar números reales.
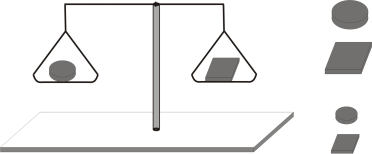
La ilustración anterior muestra una balanza de brazos desiguales que equilibra dos monedas del mismo material y del mismo espesor. La diferencia entre ambas monedas es que una es redonda y la otra cuadrada, con la particularidad de que el lado de la moneda cuadrada es igual al diámetro de la redonda. Pues bien, la proposición XII.2 de Euclides dice que esa misma balanza equilibrará cualquier par de monedas construidas con estas características, independientemente de sus tamaños. Es claro que esta analogía física nos explica el espíritu de la proposición sin necesidad de apelar a números reales. Hoy por hoy, esa proposición se escribe
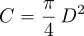
y la constante pi/4 es prácticamente la balanza de la figura.
Para poder continuar en el análisis es importante entender el alcance conceptual de las palabras usadas por Euclides en sus Elementos; por ejemplo, el manejo del adjetivo igual, sobre todo en relación a las figuras planas (entendiendo como tal lo que hoy llamamos región cerrada, un conjunto abierto conexo, incluyendo su frontera). De hecho, no se comparan figuras planas en esta obra hasta la cuarta proposición del primer libro, en la cual se demuestra nuestro actual postulado de congruencia LAL (Lado-Ángulo-Lado) sobre la base de transformaciones de movimiento en el plano. Pero la congruencia pareciera una característica que no da dificultades para admitir el uso de la igualdad; es decir, podríamos aceptar sin mayores trabas el llamar iguales a dos figuras congruentes. Pero, ¿cómo llamar iguales a un triángulo y un cuadrado?, ¿o un rectángulo y la mitad de un trapecio?, ¿o, más difícil todavía, un círculo y un cuadrado? ¿Cómo llamarlas iguales sin disponer de una referencia numérica que permita establecer el enlace?
Para resolver este problema Euclides apela a las nociones comunes: esas proposiciones aceptadas normativamente, dentro de una visión lo suficientemente amplia para que la geometría sea un campo particular de estudio. Son cinco u ocho en los Elementos: los eruditos aun discuten este número, pero nos interesan dos que se aceptan sin discusión como parte del corpus euclidiano, la 2 y la 3:
Si se añaden cosas iguales a cosas iguales, los totales son iguales.
Si de cosas iguales se quitan cosas iguales, los restos son iguales.

La figura anterior muestra cómo podrían usarse estas nociones comunes. Supóngase que partimos de las dos figuras A y B representadas en la parte superior de la ilustración. En la parte inferior, a la izquierda, tenemos dos copias congruentes (iguales) de A a las que hemos añadido B en sitios distintos, para crear las figuras C y D, que son iguales por aplicación de la noción común 2, aun cuando evidentemente no son congruentes. En la inferior derecha, a C y D les hemos restado B en sitios distintos, para obtener E y F, a las que también llamamos iguales por aplicación de la noción común 3.
Estos son los fundamentos. En la próxima entrega mostraremos cómo, en las diez proposiciones que van de la 34 a la 43 del primer libro, Euclides relaciona el triángulo con el paralelogramo para demostrarnos las diferentes formas en las que necesitaron interpretar lo que hoy abreviamos con

para el área de un paralelogramo y de un triángulo, respectivamente.
Nota aclaratoria: Las ilustraciones fueron realizadas por mí usando el programa de software libre Inkscape.
REFERENCIAS
Euclid. The thirteen books of the Elements. (Translated with introduction and commentary by Sir Thomas L. Heath. 3 volumes.) Edit. Dover. New York. 1956.
Euclides. Elementos. Traducción y notas de Marı́a Luisa Puertas Castaños. Edit. Gredos, Madrid, 1991. (Tres volúmenes).
Douglas Jiménez. El problema del área en los Elementos de Euclides. Boletín de la Asociación Matemática Venezolana, Vol. XVII, No. 2 (2010). Págs. 179-207.
Douglas Jiménez. Historia de la matemática: Pitágoras y el pitagorismo. CreateSpace.com. 2013.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Congratulations @dougjim! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
educativos acerca de la Historia de la Matemática en tanto que es muy importante conocer de donde proviene toda la maravilla que hoy enseñamos y que muchas veces nuestros estudiantes no entienden para que sirve ni de donde viene, lo peor es que muchas veces no tenemos respuestas lo cual es altamente lamentable, de allí que sus publicaciones puedan ser referencia para la comunidad de educadores en Matemática!! Mis felicitaciones y espero seguir leyendo sus detallados y nutridos aportes!! Saludos fraternos!!Hola @dougjim, creo que ha elegido muy bien un tópico de la Matemática que casi no se explora ni siquiera por los que la estudiamos y enseñamos, es precisamente su historia, creo que la comunidad de #stem-espanol de fortalece al tener un autor que desarrolle post
Gracias, @reinaseq. Tus palabras me acicatean y me comprometen.
Sí. Voy a seguir escribiendo sobre este tema que me apasiona desde mis años juveniles. La divulgación científica (en especial desde la matemática) se ha convertido prácticamente en mi actividad de trabajo.
Muy buen artículo @dougjim. Saludos.
Gracias, @tsoldovieri.