El número de oro, razón áurea o sección dorada es uno de los recursos de matemática divulgativa más manoseados. La literatura al respecto está llena de sus frecuentes apariciones en la naturaleza y sus relaciones con la sucesión de Fibonacci. Quiero dedicar entonces este post a un tema que poco he conseguido por allí: la relación de Euclides con el número de oro.
Por supuesto, me estoy refiriendo al trato que le da Euclides a este tema en sus famosos Elementos. En el post anterior hablamos del teorema de Pitágoras y de la forma en la que el alejandrino sorteó hábilmente las dificultades teóricas que tuvieron los propios pitagóricos para enfocar el teorema. Euclides lo necesitaba antes del libro V, que es donde toca el difícil tema de las razones y proporciones, pero la (supuesta) demostración original pitagórica precisaba de estos conceptos, así que Euclides hizo un hábil pase taurino que le permitió mantener el espíritu evadiendo los obstáculos. Pues bien, algo similar le sucedió con la razón áurea (de por sí una razón, tal como el propio nombre lo dice), quien hace su aparición en el segundo libro pues ha de usarse en el cuarto como ayuda para la construccion de un pentágono regular.
Este post analiza este proceso, pero primero pongámonos en autos. Un segmento cualquiera cortado en dos partes distintas de modo que el segmento total es a la parte mayor como dicha parte mayor es a la parte menor, se dice que está cortado en razón áurea. Para ser matemáticamente precisos, supongamos que (como en la figura siguiente)
el segmento original es AB y el punto de corte es C, entonces de acuerdo a la definición
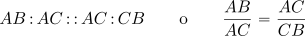
donde puedes ver, lector, que he usado la exposición euclidiana junto con su expresión algebraica actual. Esta última conduce a la famosa ecuación de segundo grado
x2 = x + 1,
cuya solución positiva es el número de oro
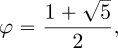
denominado con la letra griega phi en honor al arquitecto Fidias, que llenó al Partenón con este número. La razón áurea está relacionada con el pentágono regular pues sus diagonales se cortan en ella,
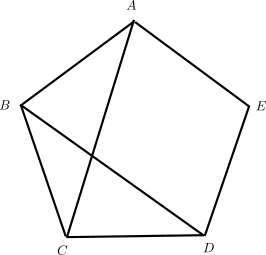
como puedes comprobar mediante semejanza de triángulos en la figura anterior.
Pero los pitagóricos demostraron que los segmentos del corte áureo eran inconmensurables, de manera que Euclides para poder entrar con esta razón en el libro II necesita recursos ajenos al concepto de razón. Por supuesto que los encontró. Veamos.
Las proposiciones de los Elementos se han clasificado en dos tipos: teoremas y problemas. Los primeros son afirmaciones apodícticas, mientras que los segundos proponen una actividad al lector, regularmente una construcción. La proposición II.11 -que es la que nos interesa- es uno de estos problemas. M. L. Puertas Castaño traduce su enunciado así:
Dividir una recta dada de manera que el rectángulo comprendido por la recta entera y uno de los segmentos sea igual al cuadrado del segmento restante.
(Observa que esto puede redactarse de manera apodíctica: "Toda recta puede dividirse en dos partes de manera que etc." Pero para Euclides la existencia de un objeto estaba ligada a la posibilidad de construírlo. Esa es la razón de los problemas. Otro detalle: la palabra recta en Euclides tiene el sentido que para nosotros segmento. La infinitud de la recta es una potencialidad de los segmentos: siempre son alargables, no importa su tamaño.)
La proporción que define a la razón áurea expresa al segmento mayor de la división como media geométrica (o media proporcional, para Euclides) entre el segmento total y la parte menor de la división; geométricamente eso significa que el cuadrado construído con el segmento mayor es igual (en área) al rectángulo construído con el segmento total y la parte menor de la división. Eso sería demostrado en las proposiciones II.14 y VI.13 posteriores, como puedes ver, a II.11. ¿Qué hace Euclides entonces para demostrar esta última? Pues... apelar al teorema de Pitágoras que, como ya vimos, era su proposición I.47. La demostración usa la figura siguiente:
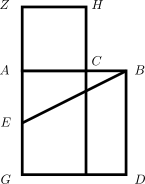
en la que AB es el segmento a dividir y ABDG es un cuadrado de lado AB. El golpe mágico de Euclides ahora es trazar el segmento BE, donde E es el punto medio del lado GA. Luego copia el segmento BE sobre la recta EA hasta Z y construye el cuadrado de lado AZ, cuyo lado AC es el segmento mayor de la división áurea buscada.
Por razones de espacio no voy a reproducir la demostración estrictamente geométrica de Euclides, más bien, te invito a leerla en la traducción de M. L. P. C. y te voy a mostrar su aritmética, tratando de que veas con ella la geometría. En primer lugar, dado que el triángulo BAE es rectángulo en A, el teorema de Pitágoras dice que
BE2 = AE2 + AB2,
pero, por la construcción hecha, es claro que
AC = AZ = EZ - AE = BE - AE,
de donde
AC2 = BE2 + AE2 -
2(BE)(AE),
que se transforma en
AC2 = (AE2 + AB2) + AE2 -
2(AE+AC)(AE),
que se reduce a
AC2 = AB2 - 2(AC)(AE),
y como AE es la mitad de AB, resultará que
AC2 = AB2 - (AC)(AB),
es decir
AC2 = AB(AB - AC),
y finalmente,
AC2 = (AB)(BC),
que es lo que dice el enunciado de la proposición.
Una observación cuidadosa muestra que el problema planteado por Euclides corresponde a una ecuación de segundo grado. En efecto, si AB = a, lo que se busca es el punto C, tal que AC = x, y
x2 = a(a - x)
o
x2 + ax = a2.
Esta última ecuación se puede convertir en la ecuación áurea, simplemente haciendo el cambio
a - x = 1.
Relación con el pentágono regular
Ya vimos que la razón áurea está relacionada con el pentágono regular, pues dos diagonales cualesquiera del pentágono se cortan en esta razón. Si te tomaste el trabajo de hacer la demostración, entonces tienes que haber observado que el segmento mayor del corte áureo de la diagonal es igual al lado del pentágono. Por esta razón (al igual que para el cuadrado) la diagonal y el lado del polígono son inconmensurables. Como ya dijimos, esto significó un fuerte golpe para la hermandad pitagórica por el sentido simbólico que, para ellos, tenía la estrella construída con las diagonales del pentágono.
Pero Euclides no tenía nada de pensamiento místico, al menos nada que pueda verse en los Elementos. Los libros III y IV están dedicados a la circunferencia (o el círculo) y la inscripción o circunscripción de polígonos a ellos. La proposición IV.10 es la primera aplicación de la razón de oro a la solución de un problema particular. (Por cierto, Euclides no usa la expresión razón de oro o nada similar relacionado con el metal amarillo. Esa denominación fue muy posterior. No es sino hasta el libro VI que el alejandrino la llama división en extrema y media razón.) ¿Qué dice la proposición IV.10? En realidad es un problema:
Construir un triángulo isósceles cada uno de cuyos ángulos de la base sea el doble del restante.
No usó Euclides elementos de precisión para referirse a los ángulos. Vale decir, no usó unidades; la metrización de la geometría fue un proceso muy posterior. Dos ángulos entre sí eran iguales o diferentes: uno mayor, otro menor. Por eso, no diría Euclides que estaba construyendo un triángulo 72-36-72, en referencia al valor en grados de sus ángulos. Ahora bien, nótese que si el ángulo de 36 grados está en el centro de una circunferencia, la base del triángulo es el lado de un decágono regular inscrito y de allí al pentágono hay un solo paso. Pero no asumamos para Euclides nuestro propio punto de vista, pues de lo que se trata es de comprender el de él.
En la demostración de este teorema Euclides necesita dos conceptos relacionados con la circunferencia, el primero de ellos es el que actualmente denominamos ángulo con vértice en la circunferencia, tal como el ángulo ACB de la figura siguiente
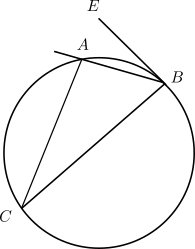
que subtiende al arco menor AB. Pues bien, en la proposición III.21 Euclides demuestra que sin importar la posición del vértice C, mientras subtienda al arco AB fijo, el ángulo resultante será igual (no variará su medida). De hecho, hoy sabemos que la medida del ángulo será la mitad del arco subtendido. Pero todavía hay más, pues en III.32 demuestra que el ángulo formado por la tangente EB y la cuerda BA es igual al ángulo en C.
Al otro concepto lo llamamos actualmente potencia de un punto respecto a la circunferencia y lo podemos ilustrar con la siguiente figura
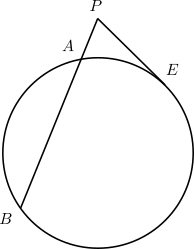
en la que se muestra un punto P externo a una circunferencia, desde el cual se trazan una secante AB a la misma y una tangente PE. El alejandrino demuestra en la proposición III.36 que el rectángulo construido con los segmentos PA y PB es igual al cuadrado de lado PE. En términos métricos y algebraicos eso significa que
(Nótese que esto implica la constancia del número (PA)(PB) independientemente de las posiciones de A y B sobre la circunferencia. Es a ese número que se llama potencia de P respecto a la circunferencia.) El recíproco del teorema también es cierto; esto es, si se cumple la igualdad, entonces PE es tangente a la circunferencia en E.
Regresemos entonces a la proposición IV.10 que nos ocupa. Lo primero que hace el sabio para la demostración es escoger un segmento cualquiera AB, que será uno de los lados del triángulo isósceles a construir. Se construye la circunferencia de radio AB y se corta este segmento según el procedimiento de II.10 (es decir, en razón áurea). Euclides se apoya en la siguiente figura:
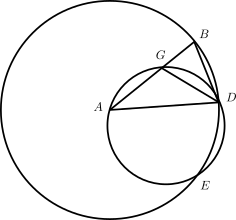
en la que el punto G es el punto de la división del segmento. A continuación se traza la cuerda BD igual a la recta (segmento) AG, se construyen los triángulos ABD y AGD y, finalmente, la circunferencia que pasa por los tres puntos A, G, D. Puesto que G es punto de división áurea en AB, entonces
y puesto que BD = AG
por lo cual, (BD)2 es la potencia de B respecto a la circunferencia menor y el segmento BD es tangente a dicha circunferencia.
Entonces, el ang(BDG) = ang(DAG), donde ang significa ángulo. Por lo tanto, podemos sumar a ambos el ang(GDA), para obtener
por lo cual, como muestra la figura,
Por otra parte, dado que ang(BGD) es externo al triángulo GAD, podemos escribir
por lo tanto
pero como el triángulo DAB es isósceles
en consecuencia
lo que significa que el triángulo GDB es isósceles, por lo cual
de donde se deduce que el triángulo AGD es isósceles, lo que lleva a
y finalmente
como queríamos demostrar.
En esta construcción el segmento BD es el lado del decágono regular inscrito en la circunferencia de radio AB, pero Euclides aún no podía decirlo de ese modo. De manera que dedica la proposición siguiente, la IV.11, justamente a la construcción del pentágono regular:
Inscribir un pentágono equilátero y equiángulo en un círculo dado.
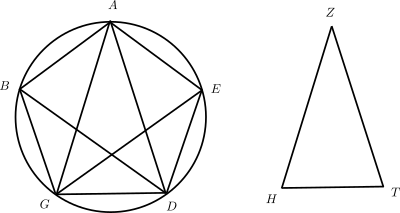
La circunferencia es dada, tal como establece el enunciado, así que Euclides contruye un triángulo ZHT con el procedimiento de IV.10, e inscribe dentro de la circunferencia otro triángulo AGD semejante a ZHT. (Procedimiento indicado en IV.2.) Luego biseca los ángulos de la base GD y con las bisectrices consigue los puntos B, E sobre la circunferencia, con lo que tiene cinco ángulos iguales, con cinco arcos consecutivos subtendidos también iguales entre sí, lo que produce cinco cuerdas consecutivas iguales entre sí: ¡Voilà! Pentágono regular.
Las tres proposiciones que siguen en el libro muestran formas distintas de inscribir y circunscribir pentágonos en la circunferencia. Estás invitado a leer.
Nota de protesta: Los desarrolladores de Steemit deben pensar en las personas que queremos escribir matemática. Hasta donde sé, el markdown debe permitir el uso de instrucciones LaTeX dentro de los documentos para producir textos matemáticos como Dios manda, pero en la realidad no conseguimos nada de esto y eso nos obliga a muchas maniobras que deberían ser innecesarias. Espero que mis lectores quieran hacer de esto una campaña, para que los desarrolladores nos faciliten la vida a los escritores de matemática.
Nota aclaratoria: Todas las ilustraciones fueron realizadas por mí con el programa de software libre Inkscape.
REFERENCIAS
Euclid. The thirteen books of the Elements. (Translated with introduction and commentary by Sir Thomas L. Heath. 3 volumes.) Edit. Dover. New York. 1956.
Euclides. Elementos (Tres volúmenes. Traducción de María Luisa Puertas Castaño). Biblioteca clásica Gredos. Madrid. 1996
Muy buen post, @dougjim. El número áureo es efectivamente una de las constantes matemáticas más famosas. Es la base de muchos patrones estéticos. Incluso, hay noticias sobre investigaciones sobre "el rostro humano estéticamente más perfecto" y lo es precisamente porque también cumple la razón aúrea en sus proporciones.
Sobre tu nota de protesta, efectivamente, este frontend de Steem aún no soporta la etiqueta math, apropiada para expresiones matemáticas. Esperemos que en el futuro las cosas sean diferentes. Saludos.
Gracias, @eniolw. Posiblemente me estés hablando de algo de lo que dice este artículo, que puse en otro de mis blogs.
Gracias también por compartir mi inquietud acerca de las facilidades para escribir matemática.
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @curie.
If you appreciate the work we are doing then consider voting both projects for witness by selecting stem.witness and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Congratulations @dougjim! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPArriba arriba @steemitvenezuela.
"Steemitvenezuela es una comunidad en crecimiento que apoya, educa y motiva a los autores con contenido en Español. Juntos somos más y con Steemit podemos lograrlo"
@erickyoussif - Equipo de curación de @SteemitVenezuela
Síguenos y apóyanos en los siguientes enlaces:
Chat de Discord | Grupo FB