The Chemistry of Music & Mathematics!-A story of their Entanglement

[etherealcreation]

The astronomer Galileo Galilei observed in 1623 that the entire universe "is written in the language of mathematics", and indeed it is remarkable the extent to which science and society are governed by mathematical ideas. It is perhaps even more surprising that music, with all its passion and emotion, is also based upon mathematical relationships. Such musical notions as octaves, chords, scales, and keys can all be demystified and understood logically using simple mathematics

The Connection Between Music and Mathematics

The famous Greek philosopher and mathematician Pythagoras once said, “There is geometry in the humming of the strings, there is music in the spacing of the spheres.” Although some may interpret this statement as mere poetry, Pythagoras was actually making a direct statement on the relationship between music and mathematics. You see, music is entirely intertwined with mathematics, so much so that even a basic major chord can be described mathematically.

History of Studying Music & Mathematics

It’s common knowledge that music has long played for performance and pleasure, yet the study of music, particularly its relation to mathematics, has been going on for equally as long as music for performance. From Greeks to Egyptians to Indians to Chinese, nearly every ancient civilized culture has examined the connection between music and mathematics. Famous philosopher Plato was known to have an extreme interest in music, particularly harmonies, and helped highlight their importance within both an individual and society. Plato wasn’t the only philosopher who found the importance of studying the relationship between music and mathematics – ancient Chinese philosopher Confucius is said to have stated that within music are a number of fundamental truths.

INTRODUCTION

Music theory has no axiomatic foundation in modern mathematics, yet the basis of musical sound can be described mathematically (in acoustics) and exhibits a remarkable array of number properties.

A little Physics! And some Musical Background

Pitch: Wave frequencies

Sound is a wave, and that the frequency of the sound is what defines the note. A sound wave creates minute pockets of higher and lower air pressure, and all the sounds we hear are caused by these pressure changes. With music, the frequency at which these pockets strike your ear controls the pitch that you hear.

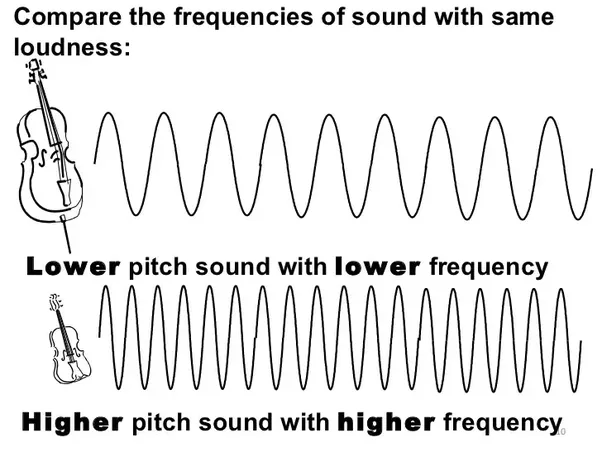
But what is frequency? It is a repetition. Imagine, for example, a bicycle wheel spinning. If this wheel completes a turn in 1 second, we say that the frequency of this wheel is “one turn per second”, or “one Hertz”.
Nice, but where is the connection with sound? Well, sound is a wave, and this wave oscillates with a certain frequency. If a sound wave completes one oscillation in one second, its frequency will be 1 Hz. For each frequency, we will have a different sound (a different note). A note, for example, corresponds to a frequency of 440 Hz.

When we listen to music, we assume that we are hearing a song or a collection of notes, but what our brains are actually processing are sound waves. For example, when a note is played, sound waves travel from an instrument and reverberates on our ear drums, and it’s the frequency of this sound wave that tells our brain which pitch or note is being played .

Mathematics in music

Octaves

No musical notes fit together better than those which are exactly one octave apart. Pairs of notes like Middle C and High C. Or Middle G and High G. Such pairs arise constantly in popular music, as in the first two notes of the third line of Happy Birthday.
Often in a symphony, one instrument (like a violin) plays a note one octave above that of another instrument (like a double bass). Piano arrangements inevitably include the same note at different octaves. What is it that makes notes one octave apart fit together so well? Consider High C, the note which is exactly one octave above Middle C.

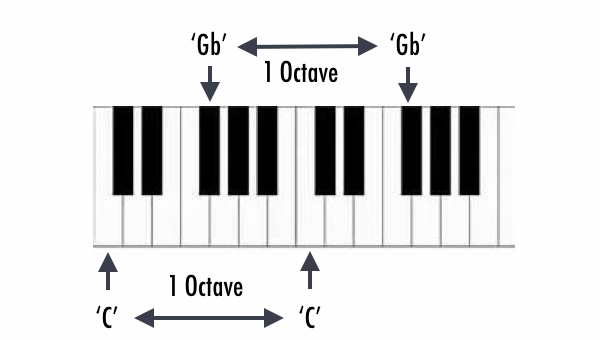
It was observed that when a frequency is multiplied by 2, the note still the same. For example, the A (440 Hz) multiplied by 2 = 880 Hz is also an A, but just one octave above. If the goal was to lower one octave, it would be enough just dividing by 2. We can conclude then, that a note and its respective note have a relation of ½.
Very well, before going on, let’s return to the past, to the Ancient Greece. In that time, there was a man called Pythagoras that made really important discoveries to Mathematics (and music). This that we showed about octaves, he discovered “playing” with a stretched string. Imagine a stretched string tied in its extremities. When we touch this string, it vibrates (look the drawing below):

Pythagoras decided to divide this string in two parts and touched each extremity again. The sound that was produced was the same, but more acute (because it was the same note one octave above):

Pythagoras didn’t stop there. He decided to experience how it would be the sound if the string was divided in 3 parts:

He noticed that a new sound appeared; different from the previous one. This time, it wasn’t the same note one octave above, but a different note, that was supposed to receive another name. This sound, besides being different, worked well with the previous one, creating a pleasant harmony to the ear, because these divisions showed till here have Mathematics relations 1/2 and 2/3 (our brain likes well defined logic relations).

One easy way to see this is on a guitar. There, pressing a guitar string at the twelfth fret cuts the string precisely in half. This makes it vibrate precisely twice as quickly. This leads to a frequency which is twice as high, and thus corresponds to a note one octave higher. For example, the first string of a guitar is normally tuned to Middle E. Playing that same string with the twelfth fret pressed produces a High E - a note one octave higher, with frequency twice as high.
In principle, we could keep increasing the octaves, and doubling the frequencies, forever - but after a certain point, the notes would be so high that only dogs could hear them.

Chord & Scale

Notes an octave apart do indeed fit together well. In a sense, they fit together too well. If you play Middle C and High C together, then there is no discordance at all. However, the result sounds sort of hollow, or even boring. More interesting combinations like chords result if we bring in other notes, too. But which notes sound good together, and which ones don't? Consider the notes Middle C and Middle G. In fact, these notes form a "fifth" interval and fit together well. We see that every second arrival for Middle C, lines up almost perfectly with every third arrival for Middle G. Once again, the two wave patterns fit well together. The two notes complement each other, rather than clashing. That is why lots of music involves the notes C and G.Since 3 time periods for Middle G

correspond to 2 time periods for Middle C, we can also say that frequency of Middle G is about 3/2 times as large as that of Middle C. Since 3/2 is a nice, simple fraction, that'swhy C and G sound good together.By contrast, the notes C and F-Sharp do not fit together well. If those two notes are combined, they don't sound quite right. They rarely appear as a pair in musical compositions or songs of any kind, at least not in a sustained way. (Well, it is true that five time periods for C isn't so far off from seven periods of F-Sharp. But it isn't so close either, and anyway, seven is too large a number of time periods to have to wait.) So, combining C with F-Sharp isn't so great, but combining C with G works well. These fundamental truths apply regardless of your musical style.

This combination of variety and consistency is just what is required to produce the C Major chord - one of the most pleasing sounds known to humanity, and the basis of multitudes of tunes from Mendelssohn to Metallica.

Key

Changing a song's key raises or lowers all the notes by the same amount. This change might make the song more convenient to play on a particular musical instrument, or more comfortable for a vocalist to accompany. If done properly, the key change should have essentially no effect on the way the song "sounds" - it should be just as recognisable, just as lovely, and just as catchy, in the new key as in the old. Indeed, it should be exactly the same song, just performed at a higher or lower pitch.

Going bit depth on Mathematics of Scales

A musical scale is a discrete set of pitches used in making or describing music. Many peoples and cultures created their own music scales.
One example is the Chinese people, which began with the idea of Pythagoras (using strings). They played C in a stretched string and then divided this string in 3 parts, like we showed before. The result of this division was the note G. Noticing that these notes had a harmony; they repeated the procedure starting in G, dividing again this string in 3 parts, resulting the note D. This note had a pleasant harmony with G and also with C. This procedure was then repeated starting in D, resulting in A. After that, starting in A, they got E. When they repeated this procedure of dividing the string in three parts once again, resulting in B, there was a problem, because B didn’t fit well when played with C (the first note of the experiment). Actually, these notes were really close one another, what caused a “sound discomfort”. Because of this, the Chinese finished their divisions getting the notes C, G, D, A and E, taking B aside. These notes served as base to Chinese Music, making a scale with 5 notes (Pentatonic). This Pentatonic Scale, for being pleasant and consonant, represented very well the Oriental Culture, which was always connected to harmony and stability. Since its creation until today, the Pentatonic Scale represents a good option to melodies, But let’s return to the subject of notes and frequencies, because we just showed 5 notes of the scale.

The Mathematics of 12 notes

The western music, which works with 12 notes, did not discard the note B as the Oriental Culture did. The western people observed that the notes C and B were close one from another and decided to create a more comprehensive scale. In this scale, all the notes should have the same distance one from another. And this distance should be the interval that had between C and B (one semitone). In other words, between C and D, for example, should exist an intermediate note, because the distance between C and D (one tone) was bigger than the distance of C and B (one semitone). Through an analysis of frequency, it was discovered that multiplying the frequency on the note B by the number 1.0595 we would arrive in the frequency of C.
Check it:
Frequency of B: 246.9 Hz
Frequency of C: 261.6 Hz
Multiplying the frequency of B by 1.0595 we will have:
246.9 x 1.0595 = 261.6 Hz (the note C).
As the goal is to keep the same relation (distance) to the other notes, we will use this procedure to discover which note will come after C. Multiplying the frequency of C by 1.0595:
261.6 x 1.0595 = 277.2 Hz (the note C sharp)
Repeating this procedure to see what comes after C sharp:
277.2 x 1.0595 = 293.6 Hz (the note D)

Notice that following this logic, we can create all the chromatic scale! In other words, after multiplying the frequency of C by the number “1.0595” twelve times, we will return to C. This is possible because “1.0595” corresponds to the result of the square root 12√2. Notice that 12√2 multiplied 12 times by itself is (12√2)12 = 2. And we already saw that a note multiplied by 2 is itself one octave above.
Now we can clearly see that these numbers didn’t come by chance. The goal since the beginning was dividing a scale in 12 identical parts, in a way that the last note return to be the first.

Logarithm in Music

We will not go in many details, but those who know a little bit about Math have noticed that we worked here with the logarithm of base 2. Because of this, the makers of piano put the form of a logarithm graphic in the piano body, to make a reference to this Musical Mathematics Discovery. Check it:
Example of a Logarithm graphic:

Piano body:

There are many other Mathematical explanations to many questions about music, but to show them here it would be necessary to talk about advanced topic in Mathematics, like Fourier series, Riemann Zeta Function, etc.we will not go more deeper. The attempt to structure and communicate new ways of composing and hearing music has led to musical applications of set theory, abstract algebra and number theory. Some composers have incorporated the golden ratio and Fibonacci numbers into their work.

• Set theory

Musical set theory uses the language of mathematical set theory in an elementary way to organize musical objects and describe their relationships. To analyze the structure of a piece of (typically atonal) music using musical set theory, one usually starts with a set of tones, which could form motives or chords. By applying simple operations such as transposition and inversion, one can discover deep structures in the music. For example, the pitch classes in an equally tempered octave form an abelian group with 12 elements. It is possible to describe just intonation in terms of a free abelian group.

• Symmetry

Music is really just a way of applying symmetry to events in time. See this delightful paper by Vi Hart about symmetry and transformations in the musical plane.

• Discrete mathematics

The pitch continuum is, well, continuous, but tuning systems and scales are discrete. The voice, fretless stringed instruments and trombones produce continuous pitches. Keyboards, fretted string instruments and saxophones produce discrete pitches. This is great intuitive preparation for the concepts of discrete vs continuous generally.

• Abstract algebra

Transformational theory developed by David Lewin allows for great generality because it emphasizes transformations between musical objects, rather than the musical objects themselves.
The chromatic scale has a free and transitive action of the cyclic group , with the action being defined via transposition of notes. So the chromatic scale can be thought of as a torsor for the group .

Real and complex analysis

Real and complex analysis have also been made use of, for instance by applying the theory of the Riemann zeta function to the study of equal divisions of the octave.

Music and Mathematics as Recreational Being

Learning to play a musical instrument relies on understanding concepts, such as fractions and ratios, that are important for mathematical achievement. But the precise relation between music and math—whether musical training promotes mathematical ability, or mathematical skill influences musical ability, or whether these skills simply develop in parallel—remains unclear.

Previous research has linked instrumental musical training to mathematical achievement, but this is highly debated. For example, students who are musically trained have been observed to have higher mathematics grades and standardized test scores, compared with students who have not studied music. Yet not all studies have found an association between these two sets of skills. Furthermore, research has yet to determine whether the proposed link can be explained by other factors, such as socioeconomic background (eg. if you grow up in a noble family, you are more likely to be able to afford music lessons, attend a good school, and so on), motivation, educational setting or overall parental involvement. To identify whether superior math abilities are a direct result of musical training, we need longitudinal studies that measure mathematical skill before and after such training and that control for

these variables.It is also possible that other cognitive factors contribute to an individual’s success in music and mathematics. In fact, research has suggested that the link may be driven by high-level cognitive-processing skills that are necessary for both subjects, such as executive functions, which allow individuals to adjust to changing task demands. Executive functions are known to be a strong predictor of academic achievement, even more so than general intelligence. Playing a musical instrument recruits these functions through, for example, constantly adjusting your motor movements to changing tempos and key signatures. To date, a few studies have suggested a link between musical training and executive-functioning skills. But longitudinal studies are also needed to establish whether this is a causal link or whether these skills develop side by side.

Lets look at a image how brain reacts while listening to music?

Conclusion

Our goal here was to show how music works mathematically and how the logical relations are understood in our brain, creating tranquility or tension. Obviously, we did everything using approximation (round numbers), because an analysis more accurate would be boring to the majority of the readers.
It is not necessary to memorize all that we taught in this topic; just think that music didn’t come from nowhere. Music is the result of a numeric organization. The interpretation of all these things is done by our wonderful and mysterious brain.

The final conclusion is that, if you are a musician, so in a way or another you are mathematician, because the feelings of pleasure that you feel while listening to music hide subliminal calculations. Your brain likes calculations, it is a calculating machine! The more you practice, study and know music, the more this faculty will be developed. Probably you will begin to feel pleasure while listening to songs that before didn’t bring great feelings to you.
We can compare this with a student of Physics in the first semester. If he reads a book of modern Physics, it will looks like Greek to him. It will not give him any pleasure. But some years later when he will have a good base of Mathematics and face this book again, maybe he can love the subject and could wish spend the rest of his life in this field.

REFERENCES:

• https://www.scientificamerican.com/article/is-there-a-link-between-music-and-math/
• https://musicedmasters.kent.edu/the-connection-between-music-and-mathematics/
• http://www.simplifyingtheory.com/mathematics-and-music/
• https://en.wikipedia.org/wiki/Music_and_mathematics
• https://plus.maths.org/c

For more discussion on this topic (or anything related to science), please join us on steemSTEM. SteemSTEM is a community driven project which seeks to promote well written/informative Science Technology Engineering and Mathematics postings on Steemit. More information can be found on the @steemstem blog.
ontent/magical-mathematics-music

Comments

[steemcleaners]

Hello,

You seem to be copying and pasting from the sources given, without writing anything original.

Copying/Pasting full texts without adding anything original is frowned upon by the community.

These are some tips on how to share content and add value:

• Using a few sentences from your source in “quotes.” Use HTML tags or markdown ">" before the quote.
• Linking to your sources.
• Include your own original thoughts and ideas on what you have shared.
• It is recommended that the quotes should not cover more than 50% of the whole post. At least 50% of the content should be original.

Repeated copy/paste posts could be considered spam. Spam is discouraged by the community, and may result in action from the cheetah bot.

If you are actually the original author, please do reply to let us know!

Thank You!

More Info: Abuse Guide - 2017.

[lemouth]

If I may comment: your post seems to be copy pasted from several sources, including:

1. http://www.simplifyingtheory.com/mathematics-and-music/
2. https://musicedmasters.kent.edu/the-connection-between-music-and-mathematics/
3. https://plus.maths.org/content/magical-mathematics-music

The first paragraph of your post comes from (1). The second and third ones come from (2). The next one from Wikipedia. Several next ones from (1), and so on. You also used (3) a lot…

I know you are mentioning those sources, but copy-pasting is not what is rewarded on Steemit. Please keep that in mind. We prefer to shed light on original content and real work. Thanks in advance for your consideration!

[mathowl]

Good job lemouth ;)

[etherealcreation]

Yes he has done his job.and...
ok you may be a phd student.we are not yet scientist to create and discover original things.We just analyse and interpret others work in our way,we try to show a whole picture by combining broken parts.
And even if we are,our that level of dedication and hardwork doesnot pays here,elsevier,aps,arxive are better platforms.And we dont research for month and years to publish here.
I am also Msc. level distinction holder physics student from TU,I too have also sound mathematical.
Better we should help and cope each other,rather than adding salt on other's pain. The day i am facing may also come to you.Chill dude,have some life

[mathowl]

So if you are using the text directly from another website you can use the Markdown notation in html. It is this button ">"

Like this!

[mathowl]

Btw I will upvote you if you write interesting posts. You don't have to discover new things. But I would love to see your perspective on science topics especially since you are a Msc. physics student. (I followed you)

Don't let this get you down. Just keep writing and improving!

[etherealcreation]

Yes I will try...but seriously to say today i don't like posting.I am here on this platform for months,invested so much time and energy,this is not paying me.I am thinking it would be better for me to engage in a job.

[etherealcreation]

Thanks ,I have just started to learn markdown.had not much idea

[etherealcreation]

that's so demotivating.I copy and pasted but there are somethings that has to be presented exactly.
What about my effort to make a whole picture by colleting parts and parts? everyone copies, they just change some sentences.What about my time and effort? I have put my full two days just to made this.Can you find this post or the way i described above in google or anywhere? you guys gave me hard punch when i was ready to have my reward.You might have suggested but not unvote.
each of other posts you have curated has also copied,If one tries to write a total original content,
wouldn't it would be like a masters thesis or a phd research? Does that much labour will worth it here?
I am very very much unhappy.
If you want to see my totally original content,why you dont saw it,i wrote 2 days before i wrote this post.
https://steemit.com/steemstem/@etherealcreation/an-extraordinary-encounter-in-physics-a-lifetime-experience

I am not boasting @lemouth , you would find very less topnotch physics guy in this whole community like me,I have a history made here in my place.ok from today I will post totally original and thought provoking content,If you cant find them it would be your weakness.As i was thinking to publish them later because of my low steem power.As it can waste my creative content due to lack of visibility.
Anyway those were my feelings, you guys are doing great work.I have nothing inside for you,dissapointment happens and it a normal thing i just expressed it.Better you should have not voted in begining than later uncurating it,if you had thought in begining it would have helped me.Because expectations hurt,for a minnow like me that amount is large and i lost it.you guys gave me hope and took it back.
But i wont give up,I will shake Steemstem community and be head of physics curation commitee soon.

[lemouth]

You presented the write-up as it was yours. This is something we (@steemstem) don't accept.

There are ways to quote stuff from other sources. If you do so, then we have no problem. You really need to present text that is taken from elsewhere as text coming from elsewhere.

Note that we didn't down vote you. We just removed a vote that we found unjustified.

If you cant find them it would be your weakness

We are humans. We do miss posts. This is what it is. What we must ensure is that the posts we found, we make them trending. For those that are missed... well... I guess this is life.

[etherealcreation]

oh yes,thats my weakness,i will study deeply to use html.But i was not claiming,if i were to present others writing as myself,would i mention it in references?
I just had no idea how to properly source it.
Here is what you might have searched for a 100% original content.
https://steemit.com/steemstem/@etherealcreation/probability-the-mathematics-that-decides-life-a-brief-research-article

[mathowl]

I know you are unhappy. But you should also view it from the perspective of all other minnows. Some of us spend long hours on original posts which go unrewarded. So if you pluck some texts of the interwebs and use that to write a posts it is very unfair on us (I am minnow too)

On a related note please check if you plagariazed in your other posts and take the suitable steps.

[muphy]

That was quite a pleasant synthesis to read.

I am a pro musician and Physics teacher, so the correlation between music and science definitely resonates with me.

A suggestion, cut your next super post in two...

[williamgabriel]

Awesome post! I'm not a musician and if I had a time machine it would be at the top of my list of things to learn as a child. Hence my focus on exposing our little girl to music every day. If you update this post or continue the topic in another post please address the effects of music on the developing brain. Math and speech are integral with music. Your research and analysis is top rate. Spread the word about music and brain development in early development (before age 3). This different than the issue of the benefits on cognitive development/function later in life which is also important. It has been shown for example the number of words a child hears before age 3 can explain the difference between future academic achievement better than economic status can. Music exposure likely fits a similar pattern. Thanks!

[etherealcreation]

yes,i beleive that music and mathematics both enhances cognitivity process because they both need lot of creativity.There is a well known effect called 'The Mozart Effect' wwwhich says listenting to opera music is advantageous for brain.I will keep posting.just need support from people like you

[resteembot]

Resteemed by @resteembot! Good Luck!
Curious?
The @resteembot's introduction post
Get more from @resteembot with the #resteembotsentme initiative
Check out the great posts I already resteemed.

[resteembot]

You were lucky! Your post was selected for an upvote!
Read about that initiative

[etherealcreation]

thanks resteembot

[xerox-bru]

How much time does it take to this this much long post. Upvoted for your hardwork.

[etherealcreation]

almost 2 day yar

[resteemr]

This post was upvoted and resteemed by @resteemr!
Thank you for using @resteemr.

---

@resteemr is a low price resteem service.
Check what @resteemr can do for you. Introduction of resteemr.

[five34a4b]

you always have great content

[etherealcreation]

i try to give my best,that's it frend :) thanks for your support

[point]

The math of notes and chords is pretty well understood. But the math of sequences of note and chords that make up a song has a lot opportunity for improvement.

Imagine a future computer program that mathematically creates quality music of your liking. Change a few parameters in the equation and out pops highest quality rock music, or country, or jazz, or blues, or classical, or surf music, or dance music, or whatever, with what we perceive as feeling.

Maybe one our genius steemian programers will figure it out for us.

[skydragon]

You got dragonized with 3.44% upvote from @skydragon, courtesy of @etherealcreation! See biddings: https://www.skydragon.me ; Delegate Steem Powers to @skydragon and Earn Profits (Details: https://steemit.com/profit/@skydragon/become-an-investor-of-skydragon-bot-service-and-earn-profits).

[abasinkanga]

This post has qualified for a resteem by the Abasinkanga Resteem Service

---

@etherealcreation just resteemed this post to 4100 followers

---

• Need a free resteem? Go here

---

• Pay for more resteems: Send 0.005sbd + post link as memo to @abasinkanga

I am not a bot. Upvote this comment if you like this service

[teamnepal]

You're one of the few promising Nepali Steemian !
Cheers !

[etherealcreation]

#thanks teamsteem

[justknecht]

Thanks for bringing this material together in a logical sequence. I've been interested in maths and music for many years, and still found some nice surprises.

I appreciated your mention of Chinese music theory. In fact, the ancient Greeks and Chinese were both independently aware of the mathematical problems of musical tuning, and Europeans and Chinese also later solved the problem through equal temperament at about the same time, also apparently independently.

From your title, I thought you might also make the connection to chemistry through the periodic table, which also proceeds in octaves of elements with similar physical qualities.

If you like synthesis across subjects, you can also add geometry: the problem of equal temperament is essentially to construct the cube root of 2, which is the same as the famous Delian problem in geometry to double the volume of a cube. Joseph Needham says the Chinese didn't have an equivalent of the Delian problem, but they had the equivalent equal temperament problem in music.

Also, more tenuously but for the pleasure of quadrivium completists, to add astronomy to the synthesis, find the orbit of the planet which will take root 2 years to rotate the sun: it's cube root 2 (Kepler's Third Law of Planetary motion, the real music of the spheres)!