Pythagorean Triples
A Pythagorean triple is a right triangle that consists integral (whole number) sides and hypotenuse. According to Pythagoras, the sum of the squares of two perpendicular legs is equal to the square of the longest leg which is called the hypotenuse. That is,
a² + b² = c².
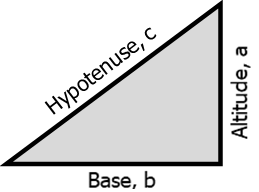
The well known Pythagorean triple is 3-4-5 triangle. That means the legs are 3 and 4 units and the hypotenuse is 5. The following are also known Pythagorean triples: 5-12-13, 7-24-25, 8-15-17, and many more.
As a mathematics enthusiast, I was curious how many Primitive Pythagorean triples are already discovered? Primitive Pythagorean triples are triangles with sides a, b, and c having no greatest common factor(GCF) other than 1. So, a 6-8-10 triangle is not counted because the sides are just multiples of 3-4-5, respectively.
I do not know what are the lengths of the sides of the Primitive Pythagorean triple that is already found out to be the one with the longest side. Answer.com states that it was the triangle with sides 77893200, 128189952, and 150000048 that is the largest so far.
Even though these don't make sense to other people, I had a curiosity that made me tabulate all the primitive Phytagorean triples by generating them with the use of VBA macros in excel. So far, I have generated 5003 primitive Pythagorean triples that have legs shorter than 50,000 units. I also include the VBA codes I used to generate these triangles.
These are the primitive Pythagorean triples that have hypotenuses less than 100.
| No. | a-b-c | No. | a-b-c | No. | a-b-c | No. | a-b-c |
|---|---|---|---|---|---|---|---|
| 1 | 3-4-5 | 5 | 9-40-41 | 9 | 16-63-65 | 13 | 36-77-85 |
| 2 | 5-12-13 | 6 | 11-60-61 | 10 | 20-21-29 | 14 | 39-80-89 |
| 3 | 7-24-25 | 7 | 12-35-37 | 11 | 28-45-53 | 15 | 48-55-73 |
| 4 | 8-15-17 | 8 | 13-84-85 | 12 | 33-56-65 | 16 | 65-72-97 |
Last 100 Primitive Pythagorean Triples with legs less than 50,000 units.
| No. | a-b-c | No. | a-b-c |
|---|---|---|---|
| 4904 | 43392-24095-49633 | 4954 | 45548-23325-51173 |
| 4905 | 43428-44525-62197 | 4955 | 45560-21462-50362 |
| 4906 | 43473-48464-65105 | 4956 | 45621-46060-64829 |
| 4907 | 43491-44620-62309 | 4957 | 45732-30115-54757 |
| 4908 | 43608-47705-64633 | 4958 | 45753-34504-57305 |
| 4909 | 43623-46864-64025 | 4959 | 45784-46287-65105 |
| 4910 | 43680-49319-65881 | 4960 | 45888-47905-66337 |
| 4911 | 43725-25172-50453 | 4961 | 45895-46728-65497 |
| 4912 | 43804-45453-63125 | 4962 | 45980-49539-67589 |
| 4913 | 43885-47532-64693 | 4963 | 46008-27206-53450 |
| 4914 | 43896-47047-64345 | 4964 | 46035-49028-67253 |
| 4915 | 43953-33896-55505 | 4965 | 46169-47400-66169 |
| 4916 | 43976-48657-65585 | 4966 | 46172-47235-66053 |
| 4917 | 43989-49820-66461 | 4967 | 46272-48865-67297 |
| 4918 | 44023-45936-63625 | 4968 | 46305-49712-67937 |
| 4919 | 44080-44799-62849 | 4969 | 46443-48076-66845 |
| 4920 | 44147-48204-65365 | 4970 | 46452-46565-65773 |
| 4921 | 44160-27387-51963 | 4971 | 46560-23236-52036 |
| 4922 | 44187-37516-57965 | 4972 | 46560-48191-67009 |
| 4923 | 44240-26718-51682 | 4973 | 46604-21597-51365 |
| 4924 | 44268-47995-65293 | 4974 | 46717-48756-67525 |
| 4925 | 44289-46600-64289 | 4975 | 46835-41652-62677 |
| 4926 | 44310-33496-55546 | 4976 | 46843-47124-66445 |
| 4927 | 44344-49617-66545 | 4977 | 46844-47517-66725 |
| 4928 | 44384-35550-56866 | 4978 | 46948-49155-67973 |
| 4929 | 44409-48880-66041 | 4979 | 46991-49440-68209 |
| 4930 | 44415-45008-63233 | 4980 | 47047-43896-64345 |
| 4931 | 44460-45731-63781 | 4981 | 47121-47800-67121 |
| 4932 | 44473-38136-58585 | 4982 | 47236-48477-67685 |
| 4933 | 44515-36612-57637 | 4983 | 47276-38493-60965 |
| 4934 | 44555-47268-64957 | 4984 | 47399-48480-67801 |
| 4935 | 44556-47333-65005 | 4985 | 47628-49445-68653 |
| 4936 | 44671-49560-66721 | 4986 | 47677-49164-68485 |
| 4937 | 44685-45668-63893 | 4987 | 47712-32825-57913 |
| 4938 | 44736-45073-63505 | 4988 | 47912-32175-57713 |
| 4939 | 44821-47940-65629 | 4989 | 47955-49852-69173 |
| 4940 | 44829-31220-54629 | 4990 | 48081-48200-68081 |
| 4941 | 44840-46671-64721 | 4991 | 48138-32600-58138 |
| 4942 | 44932-48285-65957 | 4992 | 48312-49735-69337 |
| 4943 | 45012-49915-67213 | 4993 | 48336-39010-62114 |
| 4944 | 45087-48616-66305 | 4994 | 48363-48884-68765 |
| 4945 | 45120-46009-64441 | 4995 | 48400-25359-54641 |
| 4946 | 45220-20928-49828 | 4996 | 48480-47399-67801 |
| 4947 | 45220-47619-65669 | 4997 | 48600-49049-69049 |
| 4948 | 45308-49245-66917 | 4998 | 48880-44409-66041 |
| 4949 | 45320-37791-59009 | 4999 | 49155-46948-67973 |
| 4950 | 45347-45396-64165 | 5000 | 49288-49335-69737 |
| 4951 | 45353-49296-66985 | 5001 | 49539-45980-67589 |
| 4952 | 45495-47672-65897 | 5002 | 49617-44344-66545 |
| 4953 | 45540-30749-54949 | 5003 | 49621-49980-70429 |
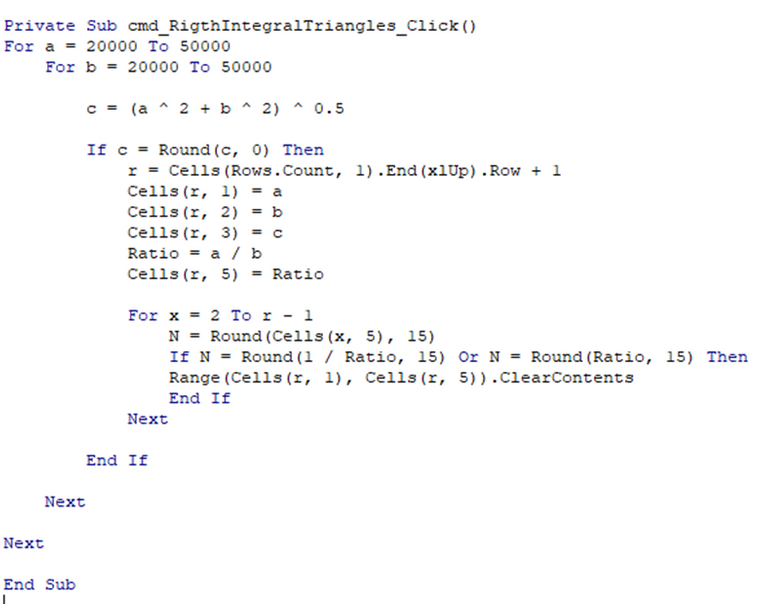
How did I generate these?
Again, I have generated the triangles with the use of VBA Macro in Microsoft Excel. The codes I used are as follows. Try to generate them even upto 1,000,000 units length. Just change the ranges of a and b in my code! :)
Wow Ser isa ka talagang lodi! hahahaha
Hahaha wala may lingaw shei. hahaha
Sir ikaw na talaga. 😊😊
hahaha. di tito boy, ikaw na!