Hello to all my dear friends of Steemit! I will begin this post with a reflection, through questions, of one of the greatest mathematicians of the contemporary age, the German David Hilbert (1862-1943):
"Who among us would not want to lift the veil behind which lies the future hidden, and look out, even for a moment, to the next advances of our science and the secrets of its further development in future centuries? What will be the particular goals that the leaders of the mathematical thought of future generations will try to achieve? What new methods and new facts will bring us the centuries to come in the wide and rich field of mathematical thought?" – David Hilbert. [1]
In this reflection, Hilbert gives us a clue about the prolific future of Mathematics and science in general, full of developments oriented without doubt, to the advancement of humanity.
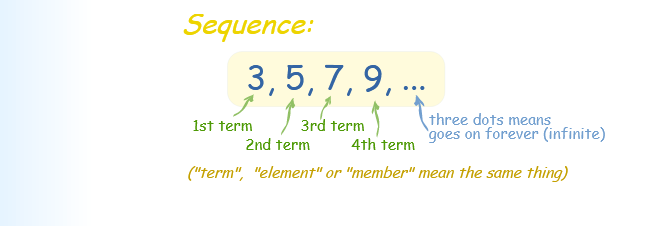
All areas of Mathematics are fertile fields where every day new knowledge of the most diverse characters is harvested: useful, powerful, curious, amazing. The field of sequences is one of them, full of so many useful and curious developments. For that reason, I will share with you, part of your wonderful results.
Sequences: Notion - Definition and Notation
In everyday language the word sequence refers to a pattern, to a succession, that is, to a set of elements, such as numbers, that meet or have an order determined, for which we can say that it has a first term, a second term, a third term, and in general, an nth term (any term).
Example 1: The well-known sequence of the natural numbers:
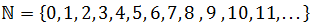
The terms of any sequence are usually denoted or represented using subscripts, as follows:
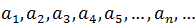
where: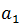 
is the 1st term, 
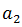is the 2nd term, and so on until 
which is the nth term, also called the general term of the sequence, since any term can be obtained from it.
Now, already known the notion of sequence, we can go to its formal mathematical definition, as a function whose domain or set of departure is the set of natural numbers (without zero) or the set of positive integers. In mathematical language:
The elements of the sequence are then those corresponding to the range of the function.
It is customary to denote a sequence in the following way: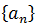 
. It is clear that a sequence is completely determined if the expression or formula of its general term is known.
Example 2: The sequence whose expression is: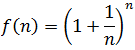 
, it can be denoted as 
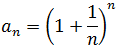or just like 
.
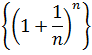The first elements of such a sequence are calculated by substituting the first values of "n" in the given expression, like this:
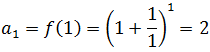
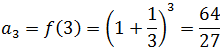
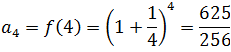
Then, the given sequence, is finally written as:
But not always a sequence is defined or determined by the formula corresponding to its general term, but it is defined in a form recursive or recurrent through a formula that relates two or more terms of the sequence, generally the nth term with some later or previous terms. Such expression is called formula or equation recurrence. When a sequence is defined recurrently it is necessary to know some of the first terms of it. A well-known example of a succession defined in this way is the so-called Fibonacci succession (which will be studied in detail in a later installment), obtained by the Italian mathematician Leonardo de Pisa, known as Fibonacci (1170 - 1240 ) "in solving a problem related to the raising of rabbits" [2].
Example 3: The recurrence equation of the Fibonacci sequence (and the first two terms) is:
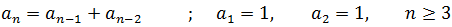
It is noted that the nth term is given by the sum of the two previous terms. For example, the third term is equal to the sum of the first and second terms, and so on.
Applying the recurrence relation, the first nine terms of the Fibonacci sequence are:
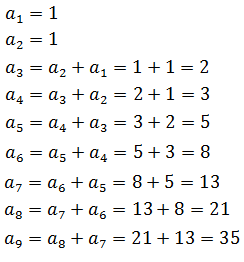
One can write, the Fibonacci sequence in extended form as:
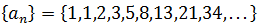
Limit of a Sequence - Convergence and Divergence
Despite having infinite terms, some sequences tend or approximate as much as desired to a value, called limit value or simply limit of a sequence (which you can see graphically in the next point). When this happens, the sequence is said to be convergent or converge to such a limit value, and otherwise it is said that the sequence is divergent or diverges.
Formally, the limit of a sequence is defined exactly like that of a function. Now, if a sequence 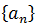has the limit L, the following can be written:
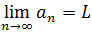
which means that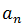 
tends to L when n tends to infinity.
It is often said that a sequence is convergent when its limit exists, and otherwise it is divergent.
The limit of the sequence of example 2 exists and is the famous number e (irrational number that plays an important role in Mathematics similar to that played by the number pi, and is the basis of the well-knowns Neperian logarithms) , that is to say:
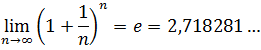
Therefore, such a sequence is convergent.
Graphics of a Sequence
Since the sequences are functions, then they can be represented graphically, which helps to visualize if they are convergent or divergent, that is, if they tend to a limit or not.
They can be graphed in the traditional way on the Cartesian plane, consisting of their graphs of isolated points on such a plane, since their domains are positive integers. Thus, the graph of the succession of example 2 is:
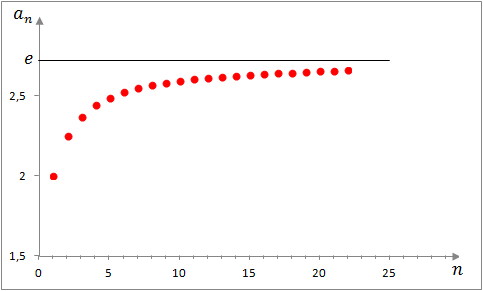
But they can also be graphed by placing their terms on a number line. This type of graphics, allows to visualize in a better way, the convergence or not of a sequence. For the sequence of example 2:
In figures 2 and 3, it is observed, as the sequence of example 2 tends to the number e.
Note: The equations were written in the Word equation editor, and figures 2 and 3 were prepared in Excel.
In the next installment, I will talk about some known sequences, the so-called arithmetic and geometric progressions.
I hope the post was of your interest and pleasure. If you have any question or suggestion, I invite you to leave your comment and I will gladly answer. Thanks for your kind reading.
Cited sources:
[1] Fundación Polar, 2004. El Mundo de la Matemática. Fascículo 1. Introducción, pp. 1. Caracas: Últimas Noticias.
[2] Fundación Polar, 2004. El Mundo de la Matemática. Fascículo 3. Sucesiones, pp. 21. Caracas: Últimas Noticias.
Consulted sources :
[3] Larson, Ron y Edwards, Bruce. 2010. Cálculo de una variable. Novena edición. McGraw-Hill/Interamericana Editores, S.A. México.
[4] Stewart, James. 2012. Cálculo de una variable. Séptima edición. Cengage Learning Editores, S.A. México.
[5] Piskunov, N. 2009. Cálculo diferencial e integral. Editorial Limusa, S.A. Madrid.
Very nice. Sequences were one of my favorite topics from calculus. Hilbert is definitely one of my favorite mathematicians up there with Gauss and Riemann.
Thanks @tensor! I confess that the sequences have also been one of my favorite themes since childhood. Definitely three great mathematicians worthy of admiration.
Ill have to follow you. I know you also write in Spanish which I sadly can't speak but I do enjoy your Mathematics and Physics based content.
I will also follow you @tensor. Yes, I also write in Spanish, it's my mother languaje. Thank you for enjoying my posts on Mathematics and Physics. Are you mathematician? Or programmer?
That is a bit of a difficult question to answer really. Yes, professionally I am a programmer, but I do have a masters in Chemical Engineering and two Bachelors one in Mathematics and the other in Physics. There was a point in time when I wanted to go the distance in academia and become a Cosmologist but through a series of rather strange incidents I ended up becoming a digital nomad. I still love to sit down and dive headfirst into theorems and I have coauthored a few Physics papers.
I guess you could say that Math and Physics were my first real passions and programming just kind of fit into the middle of all of that. Through being a programmer, I've been able to work for organizations like CERN and Fermilab.
Wow, then you are a Mathematician, a Physicist, an Engineer and a Programmer. I really feel that you are passionate about science in general.
You have worked in two of the most recognized institutes of Physics in the world, something worth admiring. I congratulate you!
As a young man I dreamed of dedicating myself to particle physics and working at CERN, but because of things in life I could not leave the country.
Very nice
Thanks @francesco.bonesi!
Congratulations @hugobohor, this post is the seventh most rewarded post (based on pending payouts) in the last 12 hours written by a User account holder (accounts that hold between 0.1 and 1.0 Mega Vests). The total number of posts by User account holders during this period was 3299 and the total pending payments to posts in this category was $4293.64. To see the full list of highest paid posts across all accounts categories, click here.
If you do not wish to receive these messages in future, please reply stop to this comment.
Thanks @bitgeek for the information!
Excellent and educational post my colleague and perijanero friend. Regards!.
Thanks for your comment colleague and brother perijanero. Greetings and hugs!