Note: This post has been updated with corrections following helpful feedback from @lemouth.
The original text is preserved and crossed to give historical context to the post.
Many thanks to @lemouth for reviewing the post.
In the past few posts I have tried to explained in my own words some of the main ideas behind Quantum Field Theory.
I would like now to examine in more details the concept of *mass and how it relates to the now famous Higgs boson.

[Image credits - Pixabay]
What is mass?
We, non-physicists-everyday-people, tend to think about mass as a quantity representing some amount of matter.
In our mind we associate mass with a number on the weighing scale in units of stones, pounds or kilograms.
But the reality is that this idea of mass is imprecise and incomplete.
Our judgement is fooled by the fact that we live in a gravitational field created by the Earth we live on.
We tend to confuse the concept of mass with the concept of weight.
When we say that we are weighing ourselves in the morning we get the result in kilograms (or stones) but this measure is actually not or weight but our mass.
Our weight is the amount of force exerted by the Earth's gravitational field on the mass in our body. If we were to truly measure our weight the result should thus be expressed in Newtons, the unit of force. (Of course never ask your wife what is her mass ;-) )
Let's stop thinking about mass as a certain quantity of matter for a minute and accept the idea that mass is a fundamental property of certain particles.
That property affects how such particle moves in a gravitational field in exactly the same way as the electric charge of an electron affects how it moves in an electric field.
Mass Energy Duality
Everyone knows Einstein's most famous equation E=mc2.
Let's now rewrite this equation as m = E/c2.
This is actually how Einstein presented the famous formula in his paper "Does the inertia of a body depend upon its energy-content? in 1905.
This tells us something about Einstein's frame of mind at the time.
Written in this way, the equation tells us that the mass of a system is directly related to the sum of all energies of its constituents.
As one can see it is also natural for scientists to express mass in gigaelectronvolts (GeVs), a unit of energy where the /c2 factor has simply been discarded.
To understand this, let's take the mass of a proton, about 0.938 GeVs.
If you read my previous posts you know that each proton is made of many quarks held together by the nuclear force carried by massless gluons
One would be tempted to think that the rest mass of the proton corresponds to the sum of all quarks' rest masses.
However this is not the case. In reality the rest mass of all quarks in the proton adds up to about 1% of the proton mass.

[Image credits Pixabay]
Where does the remaining 99% come from?
The answer lies in m=E/c2.
The mass corresponds to the sum of all energies of its constituents.
The gluons are massless and therefore travel at the speed of light within the proton and carry a huge amount of relativistic kinetic energy. This is what constitute 99% of the proton mass.
So going back to our common perception, mass doesn't represent so much a certain amount of stuff than the quantity of energy carried by the system.
99% of your mass is not matter, it's energy.
Imagine a closed box with an electric bulb inside it, and let's assume the box is being weighed on an incredibly precise weighing scale.
The implication of the above is that the box will weigh less when the bulb is turned off than when the bulb is turned on. This is because the total energy of the box is increased by the energy of the photons emitted by the bulb.
Note on the Motion of Massless Particle in a Gravitational Field
Now that we have a more accurate understanding of mass, let's review the implications on the laws of motion in a gravitational field.
In classical physics the laws of motion in a gravitational field are dictated by Newton's second law which says that the instantaneous acceleration of a body of mass m is directly related to the direction and intensity of the force it is subject to: a = F/m.
In this case F is the gravitational force (e.g. caused Earth's gravity).
From this one can derive the instantaneous velocity of the body and then the instantaneous position of that same body.
Now if this equation was entirely correct it could not explain the motion of massless particles near massive objects. a = F/m doesn't hold when m = 0.

[Image credits - Pixabay]
So how do such particles, e.g photons, travel in space?
It took Einstein's genius and incredible work on general relativity to explain this.
In general relativity the mass of objects curve space time and the total energy of a body in that field dictates how it will move.
Two things here.
First note that the term "gravitational field" is reminiscent of Quantum Field Theory. Here each point in space of the gravitational field describes the curvature of space. However gravity has not been unified with the standard model yet.
Secondly, general relativity describes motion of objects in gravitation fields in terms of their total energy, not their mass.
The total energy of a body receives a contribution from its mass at rest, mc2, but also from its relativistic momentum p.
This total energy is formulated as follows:
E2 = (mc2)2 + (pc)2
Now this is interesting because it means that for massless particles m = 0 and therefore:
E = pc.
This means that massless particles as photons have momenta directly proportional to their energy (frequency).
What about massive particles (m != 0)?
In classical physics we learn that the momentum of a body is the multiplication of its mass by its speed: p = mv.
But this relationship is only accurate at non-relativistic speeds.
Near the speed of light, the equation must be corrected with a relativistic term γ = 1 / SQRT(1 - v2/c2)
From all of the above we can see how the concepts of mass and energy are intimately related. One cannot describe the former without referring to the latter.
The Mystery of the Weak Force Gauge Bosons
 [Image credits - [Pixabay](https://pixabay.com/en/fractal-abstract-background-physics-1352598/)]
[Image credits - [Pixabay](https://pixabay.com/en/fractal-abstract-background-physics-1352598/)]
The standard model did give originally a reasonably simple pictures of particles.
Particles were divided into two groups, fermions which include mass particles, and bosons which include the gauge bosons carrying the elementary forces of the standard model (electromagnetism, weak and strong nuclear forces).
In this early picture all gauge bosons were massless and traveled thus at the speed of light.
However experimentation proved without a doubt that the weak nuclear force carrier particles, the W and Z bosons did actually have a mass of roughly 80 and 90 GeVs respectively. That's about 100 times more massive than a proton!
A big quest started in the 1960's to provide a theory that would explain why the weak nuclear force was carried by substantially massive particles.
In 1964, six physicists including Peter Higgs published a paper which proposed a solution to this problem and predicted the existence of a new quantum field, now known as the Higgs field.
Correction: The paper discussed in the above section refers to the work conducted by three independent groups consisting of Robert Brout, François Englert, Peter Higgs, Gerald Guralnik, Carl Richard Hagen and Tom Kibble.
These physicists proposed a theory describing how gauge bosons can acquire mass through interaction with a field with suitable properties (c.f spontaneous symmetry breaking).
The new field meeting this criteria became eventually known as the Higgs Field.
Like all other fields in QFT, the Higgs field can be excited resulting in a new particle to be discovered - the Higgs Boson.
A quest started then to find proof of existence of the Higgs Boson which would corroborate the reality of the Higgs field and go a long way towards validating the theory that this field is responsible for giving mass to elementary particles.
It took all the technological advances of the LHC and years of scientific research to prove in 2012 without a doubt that the Higgs Boson had been detected. Its mass was measured at around 125 GeV and is therefore very heavy.
Discovering the Higgs Boson
Nature provides several ways to produce the Higgs boson, each one with a different probability. Remember that in quantum mechanics events are usually probabilistic. The difficulty arose from the fact that, in the case of the Higgs Boson production, this probability is very very low.

[Image credits CERN]
The probability to generate a Higgs particle from the collision of two other particles is directly related to the mass of the original particles.
And so while it is theoretically possible to generate a Higgs boson from the collision of an electron and a positron (which is not too difficult), in reality the probability of doing so is extremely low because electrons are very light.
Clarification from @lemouth:
Actually, it is possible and this is one of the main motivation of some of the potential future collider experiments. The idea is not to produce a Higgs boson directly from an electron-positron annihilation, but to produce an virtual Z-boson that will radiate a Higgs (we call that Higgsstrahlung). This was also the key process to Higgs searches in the good old LEP experiments.
In practice, to increase this probability one must try to collide much heavier particles.
With this in mind, what about trying to collide heavier particles such as quarks?
What about trying to use the heaviest of all known matter particles, the top quark (170 more massive than a proton)?
But how would one accelerate two top quarks?
The problem with top quarks is that they decay extremely rapidly. It wouldn't be currently possible to inject top quarks in an accelerator and follow the same process as the LHC follows with protons.
Top quarks don't exist on their own in nature since they decay very rapidly. So scientists have to produce them in laboratories.
Scientists may collide two gluons with a certain probability that their combined energy will turn into a pair of top quarks.
As the top quark is hugely heavier than the gluon, these gluons have to be accelerated to huge speeds to provide them with enough energy to convert into a pair of top quark (remember that the total energy of the system has to be conserved, so the original kinetic energy of the gluons is significantly converted into mass energy of the top quarks).
So now we know that the most effective way to produce a Higgs boson is to accelerate and collide pairs of gluons which will sometimes produce top quarks which will then sometimes collide to produce the Higgs.
But then of course one has to produce the original gluons.
Well, gluons are abundant in protons because they hold top and down quarks together.
These gluons don't just collide with each other to produce top quarks. But a an accelerator like the LHC can collide two protons together with enough energy to cause gluons to collide with a probability high enough to produce top quarks.
So the chain reaction to produce a Higgs (with some probability) can be resumed as follows.
Colliding protons may result in gluons colliding, which may result in top quark colliding, which may result in a Higgs Boson. Phew!
This is summarised on the Feynman diagram below.
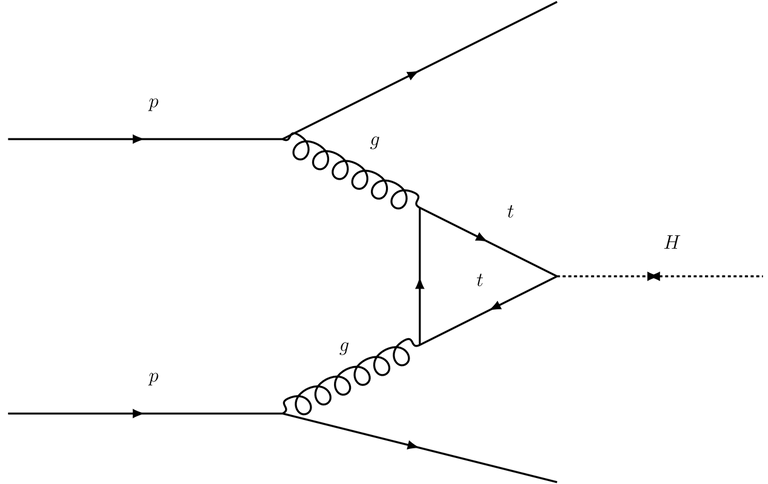
Image generated with https://feynman.aivazis.com
Assuming that a Higgs Boson is produced, how is it actually detected?
As mentioned earlier the issue is that the Higgs Boson decays very very quickly.
However the Higgs Boson has a good probability to decay into a pair of top quark and anti top quark, which will themselves decay into photons.
Correction: The above is incorrect. The Higgs boson doesn't have enough mass to be able to decay into a pair of top quarks and top quarks would decay almost in 100% of the time into a W-boson and bottom quark system.
As of today the Higgs boson has been observed through its various decay possibilities. The Higgs decaying into two photons is rare but cleaner to analyze which is why it is the preferred method.
Physicists can expect these photons to have certain characteristics such as energy and angle of motion.
The Higgs Mechanism
It is a fantastic achievement to have successfully proved the existence of the Higgs Boson.
This goes into a long way in verifying the existence of the Higgs field.
But how does the Higgs field actually explain the mass of elementary particles?
First one has to accept that the Higgs field would need to have a very significant difference with other fields described by QFT.
This difference is about the average potential energy of the field.
In other known fields such as the electromagnetic field the average potential energy is zero.
This means that in the absence of an excitation, such as an electric charge, the capacity of the field to provide energy to other particles is null.
But the Higgs field is different.
Like all other fields the Higgs field permeates all of the universe.
The key difference is that the Higgs field has a non-zero potential energy everywhere.
Why is it difficult to detect this non-zero energy everywhere?
One of the reasons behind this is that, unlike the electric field, the Higgs field is scalar, meaning that the value of the field at each point in space is just a number (not a vector), it does not indicate any particular direction in space. For this reason it cannot be detected like the orientation of an electric charge in an electric field.
But in fact we can detect the effect of this non-zero energy everywhere! It is this very energy that gives mass to elementary particles.
How?
When physicists plot the potential energy of the Higgs Field in relation to its field values the resulting graph is shaped like a Mexican hat:

[Image credits - Rupert Millard (Public Domain)]
So as one can see the minimum energy value of the Higgs field is not where the field has a zero value (top of the hat), but confined to a whole region (rim of the hat) around the value 0.
But due to the uncertainty principle every point in space is filled with an uncertain amount of Higgs energy. If this was the case for the electric field, we would say that every point of the universe is filled with an uncertain amount of electric charge.
This odd relationship between space and the Higgs field means that energy can be borrowed from the field and restituted without breaking any law of conservation.
It's as if energy can be borrowed from the Higgs field at any stage out of nothingness and given back to the Higgs field very quickly.
This may remind the reader of the concept of virtual particles appearing out of the vacuum energy fluctuations and given back very quickly to the vacuum.
This particular state of the Higgs field is called a condensate.
Other examples of condensates exist, for example superconductors can receive and donate electric charges without affecting their state.
In the case of the Higgs field, energy can be exchanged with other fields without any excitation of the that Higgs field.
So, how does a field can give mass to particles of another field?
To give some element of answer to this tricky question, let's examine the motion of an electron.
There are actually two flavors of the electron.
Electrons can spin in a clockwise or anti-clockwise direction relative the their motion.
In fact each electron constantly flips its spin from one direction to the next. In effect an electron keeps changing its identity from one type to the next.
Paul Dirac demonstrated that the mass of the electron corresponds actually to the the rate at which this flip happens.
At every moment in time, there is a probability that the electron will flip its spin.
However each time this happens, a property of the electron called the weak hypercharge is gained or lost.
Where does the weak hypercharge goes / comes from?
As you may have guessed, to and from the Higgs field.
The Higgs field being a condensate with non-zero potential energy everywhere acts as an infinite tap and sink for these hypercharges.
The electron is effectively constantly interacting with the Higgs field exchanging weak hypercharges. This slows the electron down and gives it a characteristic that we refer to as mass.
The above is a very very rough description of the Higgs mechanism, a concept that is not easy to explain and described either over-simplistically or through mathematics beyond the reach of most people.
Conclusion
This post is an attempt to shed more light on the concept of mass.
We learned that the mass of an object is not just related to the amount of material particle it carries, but also to a greater extend depends on the total kinetic energy confined within the proton by the nuclear force.
We saw that massless particles laws of motion are also affected by general relativity and such particles have a momentum directly related to their energy.
We learned a little bit about how the Higgs field and how its particle, the Higgs Boson, was discovered in the LHC.
We concluded with an attempt to understand the Higgs mechanism without which elementary particles wouldn't have mass.
Other posts in this series
- Journey through the understanding of particle physics - One
- Journey through the understanding of particle physics - Two bis
- Journey through the understanding of particle physics - Three
- Journey through the understanding of particle physics - Four
References
- Does the inertia of a body depend upon its energy-content?, Albert Einstein
- Demystifying the Higgs Boson with Leonard Susskind - Youtube
- The Higgs Mechanism Explained | Space Time | PBS Digital Studios - Youtube
- Mass in special relativity - Wikipedia
- Helicity, Chirality, Mass, and the Higgs - Flip Tanedo
Nice post! Some comments:
Strictly speaking, there are three papers, and we should talk about the Brout-Englert-Higgs mechanism to be precise (as you are Belgian, you may appreciate it ;) ). However, we talk also about the Higgs boson as this has been proposed by Higgs alone.
Actually, it is possible and this is one o the main motivation of some of the potential future collider experiments. The idea is not to produce a Higgs boson directly from an electron-positron annihilation, but to produce an virtual Z-boson that will radiate a Higgs (we call that Higgsstrahlung). This was also the key process to Higgs searches in the good old LEP experiments.
This is incorrect. The Higgs boson cannot decay into two top quarks (the Higgs mass being smaller than the top mass) and top quarks decay almost in 100% of the time into a W-boson + bottom quark system.
Today the Higgs boson has been observed through many of his main decay modes. The diphoton one is rare, but clean. Which is why it was one of the preferred mode.
Thanks for the notes and corrections.
I will make the corrections shortly in the post.
Much appreciated.
OK, I've updated the post.
Thanks again!
My pleasure!
Very interested me..
Sir ,,, I was a while ago there was building a small community. But it failed. According to our members, the great man here does not care about his member's work,
Hi @irelandscape!
Your post was upvoted by utopian.io in cooperation with steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Congratulations! Your post has been selected as a daily Steemit truffle! It is listed on rank 1 of all contributions awarded today. You can find the TOP DAILY TRUFFLE PICKS HERE.
I upvoted your contribution because to my mind your post is at least 30 SBD worth and should receive 200 votes. It's now up to the lovely Steemit community to make this come true.
I am
TrufflePig, an Artificial Intelligence Bot that helps minnows and content curators using Machine Learning. If you are curious how I select content, you can find an explanation here!Have a nice day and sincerely yours,

TrufflePig