Hello again friends of steemit
For this post I continue with the explanation of the theory of combinations previously discussed from variations, for those interested in the subject I invite you to see combinations-permutation. Recall that permutations are variations of m elements taken m to m, to form groups according to the present conditions:
- Groups with different components
- Groups with the same components, but arranged in different order
And for such processes we conclude to write the permutations in their mathematical expression in the following way:
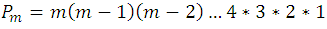
Now to define combinations groups are still forming, but under other conditions described as follows:
Given m elements, we will call domain combinations n with m
n the different groups that can be formed taking n of the m given elements, so that any two of these groups are considered different when they differ in at least one of their elements.
As you see differences in the variations in this process, it does not matter the order in which the elements are arranged. For example abcd and cadb are different variations but the same combination; only a set that contains some other element, for example, abde, is considered as a new combination.
To better understand how combinations are formed, let's take, for example and again the four letters: a, b, c, d, and write their combinations of first order, second, third and fourth. Then it turns out:
For the first order are:
For the second order, the following letters are added successively to those of the first order:
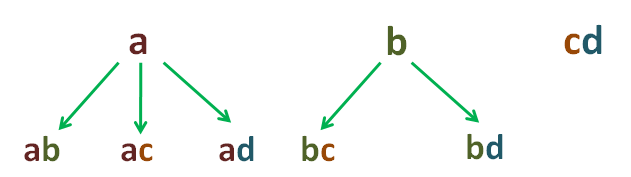
The third order combinations are obtained by adding to each of the second order the letters that follow it in succession, one by one: it looks like this:
It can be noted that the combinations ad, bd and cd, are not followed by any letter in succession, therefore there are no third-order combinations for these. The fourth order are obtained by adding the letters that follow in succession, one by one, so that we have:
It is clear that the combinations _ abd_, acd and bcd do not follow any letter in succession and therefore are discarded, then with these same observations you can make examples similar, then in general, we can say that:
- Dice m elements, combinations of order n (n
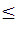m) are formed by adding to the combinations of order (n-1) the elements that follow in succession, one by one, as long as the latter exist.
Calculation of the number of combinations.
The number of combinations of order n that can be formed with m elements is designated by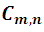 
, now to calculate this number we continue with our typical example:
In effect we consider the set formed by the elements a, b, c and d. If we form all the binary variations with these four elements, and we order them by verticals, in such a way that permutations of the same elements appear in each vertical, we have:
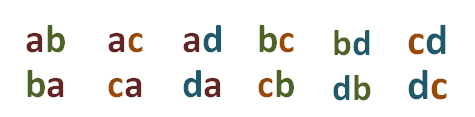
The number of these variations is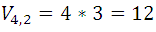 
, but of them the second order combinations of those same elements (appear in the first or second row, since they are equal a) are as many as there are columns, since when going from one to another, at least one element changes, and as each column contains the permutations of 2 elements whose number 
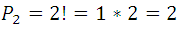, it turns out that:
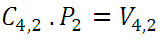
from where:
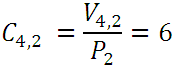
In general, each combination of order n gives rise to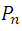 
permutations; for example, the combination of three elements, abc, gives rise to 
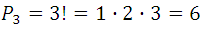permutations of three elements, which are:
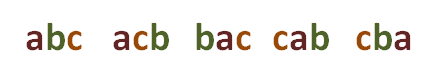
Proceeding analogously with similar examples, the following can generally be established:
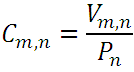
or replacing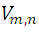 
and a 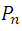by their corresponding values results:
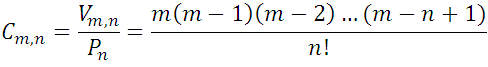
that is, the number of combinations of order n of m elements is equal to the quotient of dividing the number of variations 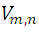by the number of permutations ..
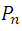For example:
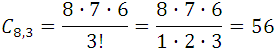
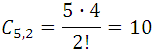
In order to give another expression to the combinations and which is well known, multiply the two terms of the fraction by the number:
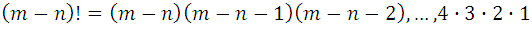
so, we have:
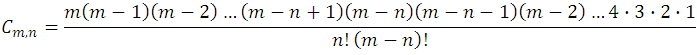
But if we look at the numerator of this new fraction it is equal to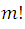 
, as it is a succession of factors of natural numbers from 1 to m; then, substituting this value in the fraction:
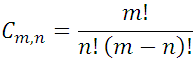
Formula, which by accepting that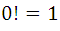 
, is valid for all possible values of n, even at the ends n = 0 and m=n.
For example, the above expression is useful for solving problems of the type:
- Calculate the number of straight lines that are formed by joining 7 points of a plane, of which there are never 3 in a straight line
Analysis: By geometry it is known that two points determine straight and only one; the order of the points does not matter, because they always determine the same line. The problem is then combinations of the 7 points taken 2 to 2. So, we have:
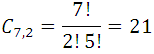
21 lines can be formed by joining 7 points of a plane.
- On a plane there are 12 points, of which there are 4 in a straight line. Calculate the number of lines that can be drawn by joining the points.
Analysis: If they were never in a straight line, the number of lines that can be drawn would be: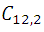 
but this number must be subtracted from the number of combinations of the 4 points of order 2 that are straight line and add the only line that results from joining these 4 points. If we denote by N the number of straight lines, we have:
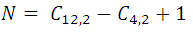
That is,
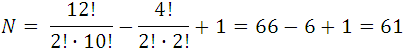
as you can see 61 lines can be formed.
This post is part of an analysis of the combinations of objects, elements or anything that can be expressed through numbers, and explained here as detailed as possible. Thank you for taking the time to see this little content and I hope it is useful or of interest to you.
Bibliography :