TENSORS. BASIC CONCEPTS. PART 1

Physical laws, if they are to be valid, must be independent of any coordinate system that is used to describe them mathematically. A tensor is a mathematical entity that generalizes the concepts of scalar, vector and linear operator in a way that is independent of any chosen reference frame. Tensioners are of great importance in physics and engineering. They are made up of N components, which are a function of the coordinates, and which are transformed by means of linear and homogeneous equations. When specifying the components of a tensor in a coordinate system, its components are determined in any other system.

SPACES OF N DIMENSIONS.

A point in a three-dimensional space is a set of three numbers, called coordinates, determined by means of a particular coordinate system or frame of reference. For example, (x, y, z), (ρ, Ф, z), (r, θ, Φ), are coordinates of a point in rectangular, cylindrical and spherical coordinate systems respectively. By analogy, a point in a N-dimensional space is a set of N numbers denoted by (x ^ 1, x ^ 2, ..., x ^ N), where 1, 2, ..., N are superscripts and not exponents.

ORDEN OF A TENSOR

The tensors can be classified by their order, according to the particular form of the law of transformation that they obey. This same classification is also reflected in the number of components that a given tensor has in a n-dimensional space.

Thus, in a three-dimensional Euclidean space such as an ordinary physical space, the number of components of a tensor is 3 ^ N, where N is the order of the tensor. According to this, a tensor of zero order is specified in any coordinate system of a three-dimensional space by a component. These tensors of zero order are called scalars, which represent the physical quantities that only have magnitude. Tensionors of order one have three coordinate components in physical space and are known as vectors.

The physical quantities that have magnitude and direction are represented by vectors.

DYAD AND DYADIC

The indeterminate product of vectors a and b is called a dyad. The indeterminate product is usually not commutative, that is, ab ≠ ba. The first vector of a dyad is called antecedent and the second is called consequential.

A dyadic D equals a second order tensor and can always be represented by a finite sum of dyads:

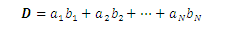
which is unique.

If in each dyad of the previous equation, the antecedents and consequents are exchanged, the resulting dyadic is called conjugate dyadic of D, which is written:

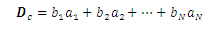
If each dyad of D in the first equation is replaced by a scalar product of the two vectors, a scalar is produced which is known as the scalar of the dyadic D and is written:

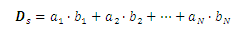
If it is replaced by a vector product of the two vectors, the result is called the vector of the dyadic D, leaving:

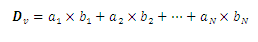
The indeterminate product of vectors obeys the distributive laws

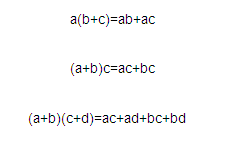
And if γ and μ are any scalars

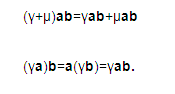
If v is any vector, the scalar products between V and D are the vectors defined respectively by:

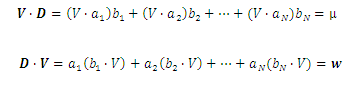
Two dyads D and E are equal, if and only if, for each vector v is met

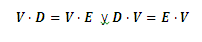
INDIRECT NOTATION. (SUM AGREEMENT)

The components of a tensor of any order, and the tensor itself, can be represented by the use of indicial notation. In this notation, letters such as subscripts and superscripts are added to the generic letter that represents the desired tensor quantity. The following tensor symbols are a clear example where the use of these indices is evident:

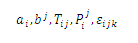
Under the rules of index notation, an index may appear once or twice in a given term. When an index does not appear repeated in a term, it is understood that this index takes the values 1, 2, ..., N, where N is an integer that determines the rank of the index. Non-repeated indices are known as free indices. The tensor order of a given term is equal to the number of free indexes that appear in this term.

First-order tensors are denoted by letters that have a free index. Thus, the arbitrary vector a is represented by a symbol that has a subscript or a simple superscript, that is, it adopts one or the other of the two forms.

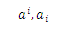
Tensorial quantities of first order are also considered, the following terms that have only a free index

The second order tensors are denoted by symbols that have two free subscripts. Thus, the arbitrary dyadic D, will appear in one of three possible ways:

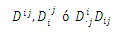
The point indicates that j is the second index. Similarly, third-order tensors are expressed with symbols with three free indexes.

When an index appears twice in a term it is to be understood that this index will take all values within its range and that the resulting terms are added together. In this addition agreement, repeated indices are called pseudo indices, since their replacement by any other letter that does not appear as a free index does not change the meaning of the term in which they appear.

Consider the expression:

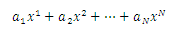
Which we can write with the use of the notation as:

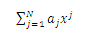
An even shorter notation is to simply write:

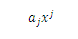
Generally the convention is adopted that whenever an index (subscript or superscript) is repeated in a given term, it must be added on that index from 1 to N.

REFERENCES:

Mase, G., 1977, Mecánica Del Medio Continuo, Libros McGraw Hill de México, S.A. de C.V.
Borisenko, A.I. y Tarapov, I. E., 1968, Vector and Tensor Analysis with Applications, Dover Publications, Inc. New York, USA.
Goicolea, J., 2002, Mecánica De Medios Continuos: Resumen de Álgebra y Cálculo Tensorial, Universidad Politécnica de Madrid, España.
Sokolnikoff, I. S., 1951, Tensor Analysis: Theory and Applications, Jhon Wiley & Sons, Inc. New York.
Murray R., Seymour, L. y Dennis, S., 1998, Análisis Vectorial, 2° edición, McGraw-Hill/Interamericana editores, S.A. de C.V.
https://en.wikipedia.org/wiki/Tensor