Hello friends of Steemit, today I present the fourth part of the basic concepts of tensors.
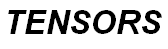
PRINCIPLE OF TENSION OF CAUCHY
In Figure 1, a continuous medium is represented occupying the R region of space, and is subject to surface forces 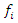 (forces acting on a surface element, either a portion of the boundary surface of the continuous medium or an internal surface arbitrary), and mass forces
(forces acting on a surface element, either a portion of the boundary surface of the continuous medium or an internal surface arbitrary), and mass forces 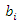 (forces acting on all the volume elements of a continuous medium). Because the forces are transmitted from one region of the continuous medium to another, the matter of an arbitrary volume V contained in a closed surface S interacts with the matter outside this volume.
(forces acting on all the volume elements of a continuous medium). Because the forces are transmitted from one region of the continuous medium to another, the matter of an arbitrary volume V contained in a closed surface S interacts with the matter outside this volume.
The average force per unit area in ΔS is given by 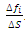 . The principle of cauchy tension states that this relation
. The principle of cauchy tension states that this relation 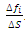 tends to a defined limit
tends to a defined limit 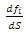 when ΔS tends to zero at point P, while at the same time the moment of
when ΔS tends to zero at point P, while at the same time the moment of 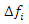 with respect to point P is canceled when the limit is taken. The resulting vector
with respect to point P is canceled when the limit is taken. The resulting vector 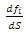 (force per unit area) is called the tension vector
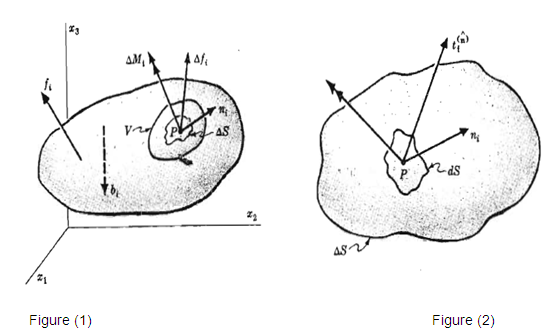
(force per unit area) is called the tension vector 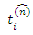 and is shown in Figure 2.
and is shown in Figure 2.
Mathematically, the tension vector is defined by
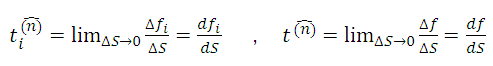
The notation 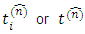 is used to enhance the fact that the tension vector at a given point P of the continuous medium depends explicitly on the particular surface element ΔS chosen and represented by the unit normal
is used to enhance the fact that the tension vector at a given point P of the continuous medium depends explicitly on the particular surface element ΔS chosen and represented by the unit normal 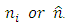 .
.
STATUS OF TENSION AT A POINT. TENSION TENSOR
At an arbitrary point P of a continuous medium, the Cauchy stress principle associates a tension vector 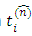 to each unit normal vector
to each unit normal vector 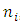 , which represents the orientation of an infinitesimal surface element containing P as an interior point, as shows in Figure 2. The totality of all possible pairs of such vectors
, which represents the orientation of an infinitesimal surface element containing P as an interior point, as shows in Figure 2. The totality of all possible pairs of such vectors  in P, defines the state of tension at that point.
in P, defines the state of tension at that point.
It is not necessary to specify each pair of vectors, tension and normal to the plane, to fully describe the state of tension at a given point.
Then, the equations of transformation of coordinates serve to relate to the tension vector of any other plane that passes through the point, with the three given planes.
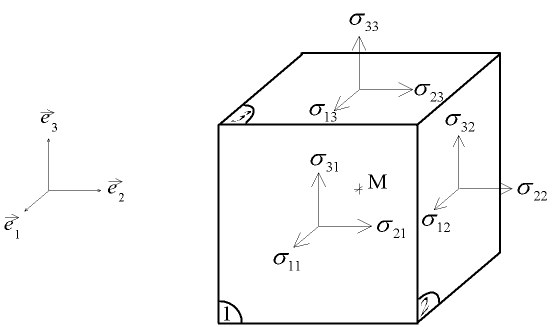
Figure 3.Graphical representation of the tension tensor components in an orthogonal base
Each of the three tension vectors associated with the coordinate planes can be written according to their Cartesian components:
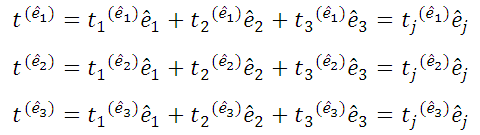
The nine components of the tension vector,  are the components of a second order Cartesian tensor known as a tension tensor.
are the components of a second order Cartesian tensor known as a tension tensor.
then, the tension tensor written in matrix form takes the form:
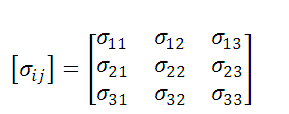
TENSORIAL FORM OF THE GRADIENT, THE DIVERGENCE AND THE ROTATIONAL
- Gradient
If Φ is a scalar or invariant, the gradient of Φ is defined by
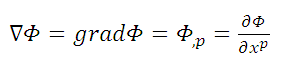
where 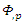 is the covariant derivative of
is the covariant derivative of 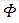 with respect to
with respect to 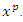 .
.
- Divergence
the divergence of 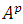 is the contraction of its covariant derivative with respect to
is the contraction of its covariant derivative with respect to 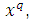 that is, it is the contraction of
that is, it is the contraction of 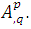 So:
So:

- Rotational
the rotational of  is
is
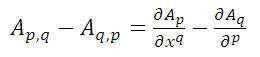
Which is a tensor of order two. The rotational is also defined as 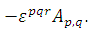
REFERENCES:
(1) Mase, G., 1977, Mecánica Del Medio Continuo, Libros McGraw Hill de México, S.A. de C.V.
(2) Borisenko, A.I. y Tarapov, I. E., 1968, Vector and Tensor Analysis with Applications, Dover Publications, Inc. New York, USA.
(3) Sokolnikoff, I. S., 1951, Tensor Analysis: Theory and Applications, Jhon Wiley & Sons, Inc. New York.
(4) Murray R., Seymour, L. y Dennis, S., 1998, Análisis Vectorial, 2° edición, McGraw-Hill/Interamericana editores, S.A. de C.V.
Figure 1 and 2 were taken from the reference (1)
Congratulations @kerlysm! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPAmazing!
Saludos kerlysm, gracias por leer mis post. Disculpa mi ignorancia eres ingeniero supongo, de qué tratan estos post?