Hola amigos de Hive Blog.
Reciban un cordial saludo.
Aunque parezca sorprendente, aun en la actualidad se desconocen o existen confusiones conceptuales referentes a uno de los movimientos al que nos enfrentamos diariamente:
La caída libre de un cuerpo
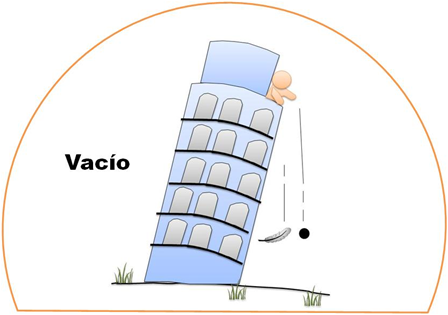
(Realizada por @lorenzor en Powerpoint)
Si formulas la pregunta en un aula de clase o al común de las personas, sobre la diferencia de tiempo con la que dos objetos con pesos distintos alcanzan el suelo al dejarlos caer desde una misma altura, la respuesta más lógica o razonable que en la mayoría de los casos obtienes, es que el cuerpo de mayor peso será el primero en hacer ese recorrido.
Cuando observamos la caída de un objeto metálico y el descenso de la hoja de un árbol o la pluma de un ave, nuestra apreciación del tiempo transcurrido de estos movimientos, nos llevan a concluir que el objeto de mayor masa desciende siempre con mayor rapidez que el más liviano.
La explicación más inmediata siempre fue atribuida a la masa de los cuerpos.
Por siglos fue aceptado, sin cuestionamiento alguno, el hecho de que los objetos de mayor masa emplearían un menor tiempo al dejarlos caer que los más livianos, hasta que Galileo Galilei refuto dichas posturas.
Basado en observaciones experimentales, Galileo Galilei fue el primero en argumentar que sin la resistencia del aire, todos los cuerpos dejados caer desde un mismo punto, bajo la acción única de la fuerza gravitacional, lo hacen con la misma aceleración, sin importar la masa que estos posean.
Es este movimiento de un objeto en ausencia de la resistencia del aire al que se conoce como caída libre.
En términos más generales, siempre que la resistencia del aire (medio) sea nula, todo objeto que sea dejado caer desde el reposo o lanzado verticalmente hacia arriba o hacia abajo, donde la única interacción del objeto sea con el campo gravitacional terrestre, tendrá un movimiento en caída libre.
Lo postulado por Galileo ponía de manifiesto que la variación de la velocidad respecto al tiempo de todos los cuerpos en caída libre era la misma, independientemente del peso de estos.
Los experimentos llevados a cabo por Galileo fueron concluyentes, demostraron con gran precisión que existía una proporcionalidad directa entre el espacio recorrido por un objeto y el tiempo al cuadrado que este emplea para recorrerlo, y en la que la constante de proporcionalidad que asocia estas variables esta ligada a la aceleración del cuerpo, conocida en la actualidad como la aceleración de la gravedad.
Es importante destacar que los resultados a los que llego Galileo fueron obtenidos en una época donde eran inexistentes los instrumentos para la medición del tiempo, y en la que aun no se disponía de herramientas matemáticas como las del cálculo diferencial o integral, con las que hoy contamos.
En este sentido, en este artículo realizaremos un pequeño análisis teórico y experimental de la caída libre de un cuerpo, en el que determinaremos el valor de la aceleración de la gravedad a partir de instrumentos de medición de alta precisión.
Fundamentos teóricos
Para facilitar nuestro análisis, consideraremos el caso de un movimiento horizontal con aceleración constante (Ver figura 2).
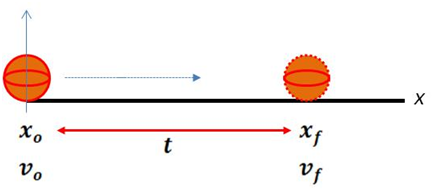
(Realizada por @lorenzor en Powerpoint)
Si un cuerpo se mueve horizontalmente con una aceleración constante, la variación de su velocidad está dada por la expresión:
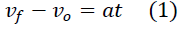

Para este caso particular de un movimiento con aceleración constante, también se cumple que la velocidad promedio  puede obtenerse según lo muestran las siguientes ecuaciones:
puede obtenerse según lo muestran las siguientes ecuaciones:
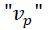 puede obtenerse según lo muestran las siguientes ecuaciones:
puede obtenerse según lo muestran las siguientes ecuaciones: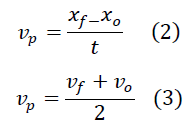
Igualando ambas expresiones se obtiene:
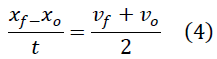
Si despejamos la 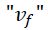 de la expresión (1) y la sustituimos en la ecuación (4) se obtiene:
de la expresión (1) y la sustituimos en la ecuación (4) se obtiene:
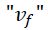 de la expresión (1) y la sustituimos en la ecuación (4) se obtiene:
de la expresión (1) y la sustituimos en la ecuación (4) se obtiene: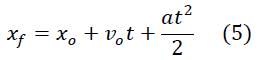
Con este resultado podemos trasladarnos al caso de un movimiento vertical con aceleración constante, donde las nuevas variables asignadas para la posición y la aceleración, son intercambiadas según se muestra a continuación:
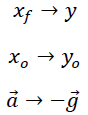
De lo que se obtiene:
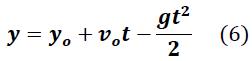
Se debe notar, que debido a que la aceleración de la gravedad es un vector que apunta hacia abajo, el signo en el último término de la expresión (6) es negativo.
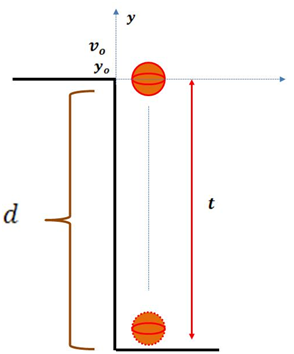
(Realizada por @lorenzor en Powerpoint)
Si el objeto en caída libre parte del reposo 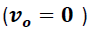 desde un punto
desde un punto 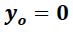 , la simplificación de la ecuación (6) nos conduce a la siguiente expresión:
, la simplificación de la ecuación (6) nos conduce a la siguiente expresión:
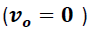 desde un punto
desde un punto 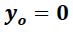 , la simplificación de la ecuación (6) nos conduce a la siguiente expresión:
, la simplificación de la ecuación (6) nos conduce a la siguiente expresión: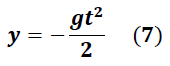
Si la distancia recorrida por el objeto se denota como "d ", la expresión (7) toma la forma:
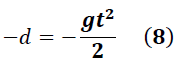
Donde, el signo negativo introducido en "d" indica que el desplazamiento a calcular está por debajo del punto de referencia yo .
De esta forma la ecuación (8) finalmente se expresa como:
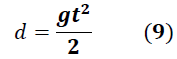
En la expresión (9) se observa claramente la dependencia entre la distancia recorrida por el objeto y el cuadrado del tiempo, tal y como lo estableciera Galileo Galilei.
Parte experimental
Metodología
En nuestro ensayo experimental procederemos a determinar la relación entre los tiempos de transito de un objeto en caída libre (resistencia del aire aproximadamente cero) y la distancia recorrida por el objeto.
En la siguiente imagen se muestra el equipo de medición de alta precisión utilizado el laboratorio de pruebas.

(Fotografía tomada por @lorenzor con la cámara de su celular)

(Fotografía tomada por @lorenzor con la cámara de su celular)
El instrumento utilizado permite registrar el tiempo de viaje de una esfera metálica para distintas alturas. En la parte superior del equipo, el sensor que sujeta la esfera inicia el registro de tiempo una vez que esta es liberada, y es detenido cuando la esfera impacta sobre un segundo sensor o plataforma colocada en la parte inferior.
Resultados
Para aumentar la certeza en la medición, se obtuvo un promedio de cuatro lecturas de tiempo por cada altura seleccionada, tal y como se muestra en la siguiente tabla:
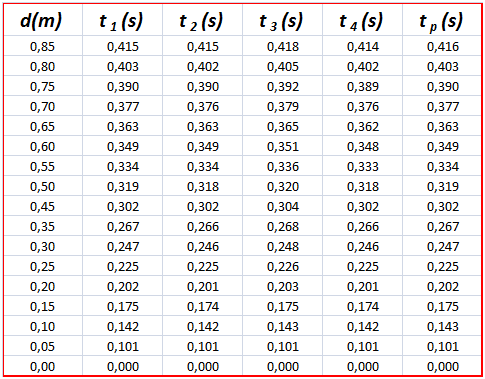
(Realizada por @lorenzor en Microsoft Excel)
Usando el programa de Microsoft Excel se construyó, a partir de los resultados obtenidos, una representación grafica de la distancia recorrida en la caída libre del objeto en función de los tiempos promedios de viaje, como se muestra en la siguiente imagen.
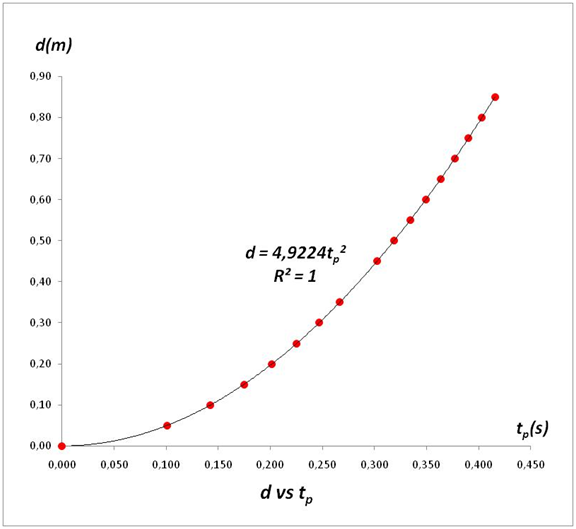
(Realizado por @lorenzor en Microsoft Excel)
En el grafico se observa que la línea de tendencia arrojada por el programa está en perfecto ajuste con los datos experimentales y la ecuación muestra un claro comportamiento de la distancia con el cuadrado de los tiempos.
Comparando la ecuación obtenida en la representación grafica con la ecuación teórica dada por la expresión (9), se observa que:
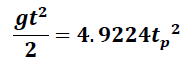
Esto implica que:
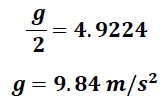
Representando este valor la aceleración de la gravedad de la esfera.
El valor obtenido en nuestro desarrollo experimental muestra una pequeña discrepancia respecto al valor teórico aceptado para la aceleración de la gravedad de 9.81 m/s2, validando la metodología y principios usados en nuestro análisis.
Cabe destacar que la aceleración de la gravedad varía según el punto geográfico donde esta se mida, siendo afectada por la altitud o latitud del punto de medición.
Conclusiones
● Los resultados obtenidos muestran una clara dependencia de la distancia con el cuadrado de los tiempos y confirman que la aceleración de la gravedad es constante e independiente de la masa del cuerpo en una caída libre, validando las observaciones y resultados obtenidos por Galileo Galilei.
● La metodología empleada en nuestra investigación puede implementarse como una alternativa en el aprendizaje de la Física, con el objeto de profundizar sobre los principios inherentes a un movimiento en caída libre.
Referencias
- Física para Ciencias e Ingeniería. Fishbane, Gasiorowicz, Thornton. Volumen I. Prentice Hall.
- Física para Ciencias e Ingeniería. Raymond A. Serway, Robert J. Beichner. 5a edición. Tomo I. McGraw-Hill.
- Física Universitaria. Sears Zemansky, Young Freedman. 9na edición. Volumen 1. Addison Wesley Longman.
¡Felicidades! Esta publicación obtuvo upvote y fue compartido por @la-colmena, un proyecto de Curación Manual para la comunidad hispana de Hive que cuenta con el respaldo de @curie.
Si te gusta el trabajo que hacemos, te invitamos a darle tu voto a este comentario y a votar como testigo por Curie.
Si quieres saber más sobre nuestro proyecto, acompáñanos en Discord: La Colmena.
Gracias por el apoyo.
Curation Collective Discord community
community witness. Please consider using one of your witness votes on us hereEste post fue compartido en el canal #spanish-curation de la comunidad de curación y obtuvo upvote y reblog por la cuenta de la comunidad @c2-spanish después de su curación manual.This post was shared in the #spanish-curation channel in the for curators, and upvoted and reblogged by the @c2-spanish community account after manual review.@c-squared runs a
Gracias por el apoyo
Congratulations @lorenzor! You have completed the following achievement on the Hive blockchain and have been rewarded with new badge(s) :
You can view your badges on your board And compare to others on the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Do not miss the last post from @hivebuzz:
Support the HiveBuzz project. Vote for our proposal!
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider supporting our funding proposal, approving our witness (@stem.witness) or delegating to the @stemsocial account (for some ROI).
Please consider using the STEMsocial app
app and including @stemsocial as a beneficiary to get a stronger support.
g de manera experimental. Recientemente vi un pozo subterráneo abandonado el cual al acercar el oído aun escuchas algo de agua fluyendo. Entonces recordé que del libro de Física de Serway una vez resolví un ejercicio relacionado a medir la profundidad de un pozo. Entonces lancé una piedra y medí el tiempo en que escuchaba la piedra caer en el agua utilizando la ecuación (9). Resulta que recordé que el sonido también tarda un tiempo en llegar arriba, así que hice los cálculos (un poco complejo el despeje tomando en cuenta esto de la velocidad del sonido) y lo que originalmente eran algo así como 3,5 segundos resultaron ser aproximadamente 3,2 segundos... en fin bastante útil lo que es la Física y como puedes aplicarla en el entorno.Saludos @lorenzor muy bien explicado como obtener el valor de
Gracias por el apoyo y la visita. Ese problema que planteas es un muy buen ejemplo de las aplicaciones de este movimiento en caída libre. Gracias
Excelente post mi amigo @lorenzor. Muy bien presentado y didáctico. Mis felicitaciones. Te invito a ver mi nuevo post https://hive.blog/stem-espanol/@tsoldovieri/conceptos-fundamentales-de-la-termodinamica-parte-1. Saludos!.
Saludos estimado amigo. Gracias por su comentario. Me alegra que también este de Regreso. Siguiendo sus trabajos como siempre.
Saludos @lorenzor, felicitaciones
Gracias por socializar otra de tus destacadas entregas.
✍ A modo de recordatorio, este jueves 04 de junio, a partir de las 16:00 hrs (04:00 pm) hora de Venezuela, se retomarán los Conversatorio Virtuales, actividad que estará desarrollando el Dr. Tomás Pérez, habrán 3 sorteos de 5 Hive para los usuarios que asistan a esta interesante actividad académica.
Saludos . Gracias por el comentario y tu visita. Complacido de estar de regreso y compartir con esta prestigiosa comunidad. Gracias por el apoyo y la invitación.
Congratulations @lorenzor! You received a personal badge!
You can view your badges on your board And compare to others on the Ranking
Support the HiveBuzz project. Vote for our proposal!