A mathematician I follow on Twitter recently referenced On Determining the Irrationality of the Mean of a Random Variable by Thomas M. Cover (The Annals of Statistics 1973, Vol. 1, No. 5, 862-871).
Testing Coin Flips for Rationality
This paper makes a surprising claim: it is possible to test whether the mean value of random variable lies on a countable set of the real number line. "Countable" means a set with the same cardinality as the natural numbers, such as: the integers, the rational numbers, the algebraic numbers, or the computable numbers.
The example Dr. Cover gives is a coin flip. A fair coin has probability p=0.5 of coming up heads. But an unfair coin could have probability p=0.4, or p=1/7, or p=sqrt(2)/2. Given a sequence of N results of our coin flip, can we reject the hypothesis that p is rational, and conclude that it must be irrational?
The reason this seems unlikely is that after any finite number of coin flips, the proportion that are heads must be a rational number. So how would we ever conclude that the underlying mean value is actually irrational?
Cover's main result is the following theorem:

There's a lot to unpack here. We have a countable set of hypotheses H_i, that the mean value (the probability) is equal to some number in the set S, and a null hypothesis H_0 that the mean value isn't in that infinite set at all.
The operator i( x, delta ) finds the earliest element in the list S that is within distance delta of x, that is, the minimum i such that | x - s_i | < delta. The mean value x and the delta are indexed by a function of the number of samples that we take (we're not allowed to change our mind after every sample.) The resulting position in the list S is compared with an increasing value k. If the position is greater than k, we reject the hypothesis that the mean value is in the list at position s_i, and instead say that the mean value isn't anywhere in the list. If the position is less than k we reject the null hypothesis and say it is likely that the mean value is in the list, and further that it's s_i.
The remaining conditions are technical limits on how fast delta decreases and k increases; if followed, they ensure that the procedure "works." But there's a lot of weasel words in "works" that we'll come back to later: "a finite number of mistakes" and "except for a null set."
The idea here is that we're using the list of possible mean values S as if it is ordered in increasing "complexity". If we find a match but it's too complex, we probably shouldn't use that match as an explanation of the data. For example, if we find that the probability of getting heads is about 0.3141592653589, which is more likely? That it's actually the rational number 3141592653589/10000000000000, or that the mean value is an irrational value, say, pi/10?
Or to put it in non-math terms, if you have a list of excuses:
(0) I didn't do my homework
(1) I did my homework, but it got soggy in the rain
(2) I did my homework, but my dog ate it
(3) I did my homework, but I forgot it at home
(4) I did my homework, but my sister ate it
...
(454) I was prevented from doing my homework, because I was kidnapped by space aliens.
(455) I'm actually a time traveller from the future, so I've already turned in my homework
(456) Somebody I know on Steem beat me up and took my homework
then the decision procedure is to demand more evidence for hypotheses further down the list.
Strangely, the order of the list doesn't actually matter. If your hypothesis is true, then eventually (after only "finitely many errors") you will have enough evidence that you can reject the null hypothesis. So while the motivation is complexity, the theorem doesn't actually depend on ordering the countable set by complexity at all; you just have to order it in some way.
Testing decimal digits for rationality
A corollary provides a way to test numbers for rationality, given a digit at a time:
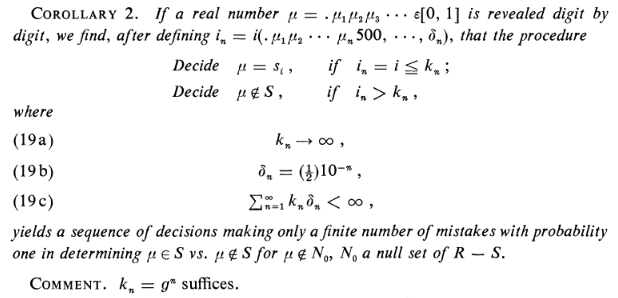
The procedure is to look for the "first" rational number that agrees with the input on the digits we have so far. If the position of that rational number on our list is too large, then reject that match until we accumulate new digits, and instead mark the number as irrational.
I implemented this test using the standard enumeration of the rationals between 0 and 1, in order of increasing denominator:
0, 1, 1/2, 1/3, 2/3, 1/4, 2/4, 3/4, 1/5, 2/5, 3/5, 4/5, 1/6, ...
(Convince yourself that every rational number between 0 and 1 is on the list somewhere; some of them are there twice, but that's OK.) It's always possible to just walk the list in order, but this ordering has a particularly efficient lookup procedure based on continued fractions; see https://www.quora.com/Given-an-enumeration-of-the-rationals-in-0-1-what-is-an-efficient-way-to-find-the-first-rational-number-within-a-given-distance-of-an-input-real-number/answer/Mark-Gritter
How well does this procedure do? Let's give it a bunch of irrationals. The scale at the top is the number of digits tested, and "I" means the test says that number is irrational, "R" if rational.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
cos( 1*pi/40 ) R R I I R I R I I I I I R I I R I I I I I I I I I I I I I I R I I I I I I I I I 0.996917333733127976197773408742044420158927
cos( 2*pi/40 ) R I I R I R I R I R I I R I I I I I I I I I I I I I I I I I I I I I I I I I I I 0.987688340595137726190040247693437260758407
cos( 3*pi/40 ) R I R I I R I I R I I I I R R I I I I I I I I I I I I I I I I I I I I I I I I I 0.972369920397676601833645834118797644002576
cos( 4*pi/40 ) R I I I I R I I I R R I I I I R I I I I I I I I I I I I I I I I I I I I I I I I 0.951056516295153572116439333379382143405699
cos( 5*pi/40 ) R R R R R R I R I I I I R I R I I I I I I R R I I I I I I I I I I I I I I I I I 0.923879532511286756128183189396788286822417
cos( 6*pi/40 ) I R R R I I R I I I I I R I I I I I I I I I I I I I I I I I I I I I I I I I I I 0.891006524188367862359709571413626312770518
cos( 7*pi/40 ) I R R R I I R I I I I I I R I I I I I I I R I I I I I I I I I I I I R I I I I I 0.852640164354092221519383458130412135817266
cos( 8*pi/40 ) I R R R I I R R I I I R R I I I I I I I I I I I I I I I I I I I I I I I I I I I 0.809016994374947424102293417182819058860155
cos( 9*pi/40 ) R R R R I I I R I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I 0.760405965600030938174594364844901999888747
cos( 10*pi/40 ) R R I I R I I R I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I 0.707106781186547524400844362104849039284836
cos( 11*pi/40 ) R I R R R I I I I I I I R I I I I I I I I I I I I I I I I I I I I I I I I I I I 0.649448048330183655726320770893762879277503
cos( 12*pi/40 ) R R I R R I I R R I I I I I R I I I I I I I I I I I I I I I I I I I I I I I I I 0.587785252292473129168705954639072768597652
cos( 13*pi/40 ) R I I I R I I I I I I I R I I I I I I I R R I I I I I I I I I I I I I I I I I I 0.522498564715948864987897880178293823415387
cos( 14*pi/40 ) I R I I I I R I I R I I I R I I I I I I I I I R I I I I I I I I I I I I I I I I 0.453990499739546791560408366357871198983048
cos( 15*pi/40 ) R R R R I I R I I I R I I I I I I R I I I I I I I I I I I I I I I I I I I I I I 0.382683432365089771728459984030398866761345
cos( 16*pi/40 ) R R I R R I I I I R I I I I I I I I I I I I I I I I I I I I I I I I I I I I I I 0.309016994374947424102293417182819058860155
cos( 17*pi/40 ) R R R I R R I I I I R I R I I I I I I I I R I I I I I I I I I I I I I I I I I I 0.233445363855905411767744430202870848785742
cos( 18*pi/40 ) I R R I I I R I I I I I I I R R I I I I I I I I I I I I I I I I I I I I I I I I 0.1564344650402308690101053194671668923139
cos( 19*pi/40 ) R R R R I R I R I I R I I I I I I I I I I I I I R I I I I I I I I I I I I I I I 0.0784590957278449450329602459934596986819558
These numbers are all provably irrational, but the test still made a mistake at 35 digits. How about rational numbers?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
R R I I R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R 0.00729927007299270072992700729927007299270073
R R R I I I I R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R 0.0001220703125
R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R 0.571428571428571428571428571428571428571429
R R R R R R R R R I I I I I I I I I R R R R R R R R R R R R R R R R R R R R R R 0.999999999
R I I R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R 0.0103092783505154639175257731958762886597938
R I I R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R 0.0655737704918032786885245901639344262295082
R R I R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R R 0.915254237288135593220338983050847457627119
The numbers are 1/137, 2^(-13), 4/7, 999999999/1000000000, 1/97, 4/61, and 54/59. (Some of these were picked because they have long repeating decimals. The test works well in these cases because it finds the rational number itself on the list fairly quickly, and then evidence starts to accumulate that this was the right choice as more and more digits agree. Only "unlikely" fractions, ones with large denominators, cause any problem at all. 999999999/1000000000 is the 499,999,999,500,000,002th number on the list; 2^(-13) is only 33,542,148.
Source code:
Getting back to those weasel words
How many errors is "finitely many"? The test doesn't specify. In fact, no error bound or confidence is presented at all, because the performance of the test depends entirely on how the countable list is ordered. You can push the fraction 1/2 back further and further in the list to create more and more errors for 0.5000000000000000000000000000....
Eventually you have to list 1/2, and sometime after that the test will acknowledge that the input number is probably on the list. But that could be after thousands, or millions, or googols of errors. The test simply doesn't say anything meaningful at all about how likely it is that your test at N=40 is successful; it just says that as N goes to infinity, you'll eventually stop making errors (with probability 1, which is a whole other can of worms.)
Except, that guarantee comes with fine print too, for any number except those in "a null set", or as it appears in other contexts, "a set with measure 0". But that set could be countably large! That is, the cases where the test fails to meet its guarantee of finitely many errors could be just as large as the set of hypotheses you're trying to test. Any number we could possibly test could be in that set, because humans and computers can only describe countably many numbers. If we pick a random number, it's certain we won't pick something in a null set, but that's it. Any "interesting" number we name might well be one that the algorithm can't get right!
So, forget about applying the test to famous unsolved problems. You really don't get much more out of it than you put in. But, the exercise of making Occam's Razor into a statistical test is interesting, and this paper has been cited many times over the years.
The paper concludes by investigating physical constants; how much precision should we demand before giving some credence to a complicated formula that produces them from other constants? Dr. Cover concludes that a particular example is far from simple enough to be justified from the (then-)current accuracy of the measurement:
The theoretical physicist's burden in this problem is to show that [the formula] is not as complex as it seems, by showing how it may be simply derived with the aid of "known" physical laws. In other words, we allow some juggling of the order of the list as a concession to common sense... The burden on the experimentalist is to reduce the experimental error. This will allow formulas of higher complexities to be considered as explanations and will also eliminate incorrectly held theories of lower complexity.
He also notes that some sets we might wish to test, such as the set of all computable numbers, are countable but can't be effectively enumerated. So it's not possible to use the test against the computable numbers, unless an Oracle gives us the enumeration. The barrier here is that a computable number is generated by a single Turing machine accepting input N and returning the Nth digit. But we can't in general prove that a Turing machine halts on all inputs; a candidate number might turn out not to be computable after all if its Turing machine fails to halt for sufficiently large N.
This story was recommended by Steeve to its users and upvoted by one or more of them.
Check @steeveapp to learn more about Steeve, an AI-powered Steem interface.
Hi markgritter,
Visit curiesteem.com or join the Curie Discord community to learn more.
I guess this subject is covered on Statistics and Probability.
I sequence of numbers theories maybe applied here.
So this for sure a probability subject....and getting it is always a mystery. I know many love this topic in Mathematics but for me it's simply...shoooo
This post has been voted on by the SteemSTEM curation team and voting trail.
If you appreciate the work we are doing then consider voting us for witness by selecting stem.witness!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
I didn't know that paper. That is a fun result. It reminds me a bit of the miller-rabin test for prime numbers. This test checks how probably it is that a number is a prime.
isn't on the list, then we'll make only finitely many mistakes.To me it feels a little bit like Levin's universal search (https://www.quora.com/How-is-it-possible-that-an-existing-algorithm-solve-NP-complete-problems-in-polynomial-time-if-and-only-if-P-NP/answer/Mark-Gritter) in that it keeps ticking things off an infinite list. If the right answer's there, then we'll get to it eventually. The clever bit is ensuring that if the mean value
Few years ago i would be more than intrigued with these theorems, right now i'm trying to figure out how to apply it to wealth making, in a legit way. Lovely topic @markgritter