You could also think about limits as a mathematical object which tells you how to make a function continuous.
can be extended to the function 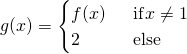
Observe that this function is continuous.For example in your case f(x) = 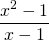
In the case when you are dealing with infinity there are mathematical methods which let you apply the same trick.
This is the reason why we consider limits for functions.
First of all, sorry for the late reply
and secondly, thank you for the suggestion.
The suggestion above is related to continuity of the function. I wanted to focus on the just basic concept of limit. Continuity of the function is whole another part. So, if I I ever write about it, I will surely add this.
I think I have properly defined infinity in this post. How to tackle that can be subject of the next post.
You can substitute continuity in my reply by approaching something. It is not necessary to define it formally.
In terms of a series or sequence your approach makes sense since they are discrete since they are evaluated for 1,2,3,4 etc. But limit in the sense of this function f that you used is in a sense different since you are relying on its continuity by approaching in a continuous sense a certain value.
The point of using that example was that the limit can exist without function being continuous. we can intuitively see the function is not continuous at x =1, but we are not interested at exactly that point. We are interested in how the values are approaching. I may be relying in the concept of continuity at other points than x=1, but I still dont know why should I make function continuous at x=1.
I think you misunderstand my previous comment.
If a function is defined in some interval then the concept of limit is a bit different because you can use different ways to approach the same point. While if it is only discretely defined you can only do this over the integers. So my claim is that it is better to keep it in a discrete setting if you only define the limit in a discrete setting