Is The Universe Infinite?

We know that the universe is the collection of all space and time. We also know that the universe has a high probability of taking on 3 different geometric bodies: flat, spherical, and negatively curved. Its geometric shape is dependent on how much density the universe holds; since we cannot measure the density of the universe we do not know the shape of the universe.

Assuming the universe follows the rules of Euclidean space and holds no curvature a question that many scientist wonders: is the universe infinite? If our hypothesis is the universe is infinite that would mean our alternative hypothesis would be that the universe is finite, and I can assure you both assumptions hold brain twisting conclusions. Consider that; we also do not know if the universe is finite or infinite is size, similar to how we do not know the shape. However, there is plenty to analyze about our observable universe to formulate a solid hypothesis.

Media Source: https://www.zacharyfeder.com/

Let's further define Euclidean space: Euclidean space does not mean 2 dimensional. Euclidean space encompasses the two-dimensional Euclidean plane and the three-dimensional space. Relating to our universe; zero curvature does not equal empty height. We obviously have depth in our universe, we can move up, down, left, and right within space. Consequently, we can derive the Cartesian space by assigning a coordinate system to the Euclidean space! The Cartesian plane encompasses the Euclidean plane with one fixed method of representing points. That method of representing points is known as the Cartesian coordinate system where the x, y, and z axis relatively represents right, left, up, down and depth.

The Cartesian coordinate system is widely used around the world for many practical applications, but this does not accurately represent the universe as a whole. Consequently, the Euclidean plane is a more general representation of space that holds a negatable bias which allows us to better represent the geometry of the universe. A better way of thinking about this, is by asking yourself: which way is down? The answer to that question depends on your relative position. Generally, if you're on Earth's North Pole, "down" would be towards the South Pole, however if you're on the South Pole "down" would be towards the North Pole. This is because "down" on Earth means pointing towards the Earth, where the core of the Earth represents our origin.

Media Source: https://commons.wikimedia.org/

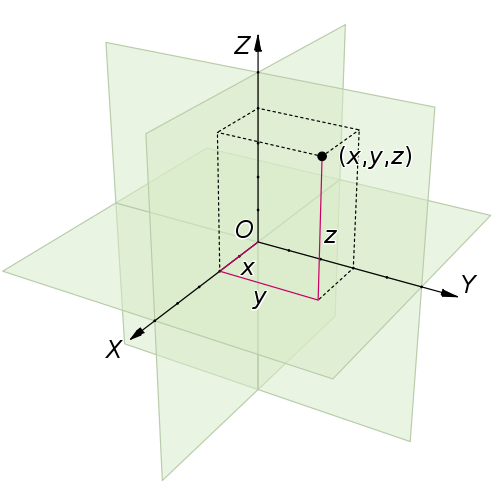
Why do we care about this? Well in our universe it's hard to state what the origin may be. We could provide a local origin for smaller systems such as our solar system because we can place our entire solar system on a plane and pinpoint the center. We can't put the entire Universe on a plane because we can't see the entire Universe, only a "small" portion of the universe is observable due to a multitude of factors. These factors include but are not limited to the expansion of space, limited technology and the speed of light.

Our question lies beyond the observable universe, and either proposes there is a finite or infinite amount of space and time. If the universe is finite, we can either loop back around or if the universe is flat (our assumption in this article) we would reach the 'end'. It's difficult to imagine what would be at the 'end' considering two variables: light, and the expansion of space. What would we see at the edge of the universe if there was an end? A bunch of trapped matter, and light? Would everything be at a standstill at the edge of the universe? What's preventing the universe from expanding more, a void wall? Yes, we could abide by the law of conservation of mass and state defiantly matter cannot be created nor destroyed because there is finite amount of space available. Obviously, there is plenty to ask and no answers available but it really gets you thinking.

the-edge-of-the-universe-is-closer-than-scientists-previously-thought.jpg

Media Source: http://www.businessinsider.com/

Analyzing our hypothesis that is; the universe is infinite, leads to some strange outcomes. If the universe is infinite that means there is an infinite amount of space and time, that also means that light can continuously travel in one direction without ever making it’s way back to where it was or reaching a stop. This would mean that space and time would go on forever and see no end. Sounds relatively reasonable right? That is, until ‘you’ decide to take a journey out into the universe and document what you would observe. Let’s make a few impossible assumptions; you are traveling the speed of light, you never age, nor can you die. As you are traveling across the universe consider that there is a set amount of combinations and permutations in which matter can reorganize itself.

This is important because matter can only reorganize itself so much before it starts forming duplicates. As far as we know, this includes all matter in all of the universe. This means the more you travel outwards, the more familiar the universe may appear. You could potentially observe an identical pile of hydrogen that you saw near Earth. The more you travel, the more familiar things will appear to the point where matter would have replicated itself and you may see a duplicate version of the Milky Way, Earth or even yourself. If you were to keep traveling outwards, and continue to collect yourself on the way there you could potentially have an infinite amount of ‘you’ in an infinite universe.

Media Source: https://fineartamerica.com/

The realistic probability of finding a duplicate version of yourself is relatively low; that is by the time we could travel that far out into the infinite universe, Earth would be probably be gone. We don’t come close to the speed of light, and we obviously age. Even if we could travel at the speed of light it would take us 13+ billion years to get to the end of the observable universe. However, if the universe truly is infinite; these are only a couple of the strange things you could expect to see in our infinite collection of space and time.

TL;DR: We know that the universe is the collection of all space and time. We also know that the universe has a high probability of taking on 3 different geometric bodies: flat, spherical, and negatively curved. We are going to explicitly analyze the potential for an infinite vs. finite Euclidean universe. An Euclidean universe simply means that it follows the rules of Euclidean space, and has no curvature. This does not mean an empty amount of depth, as we can obviously displace objects in all 3-dimensonal directions. The Euclidean space encompasses the two-dimensional Euclidean plane and the three-dimensional space.

Assuming that our universe is finite; we can either loop back around or if the universe is flat (our assumption in this article) we would reach the 'end'. It's difficult to imagine what would be at the 'end' considering two variables: light, and the expansion of space all of which would be trapped at the edge of the universe because we assumed the universe does not loop. This means that we could theoretically measure all of the matter, space and time the universe holds.

Analyzing our hypothesis that is; the universe is infinite, leads to some strange outcomes. This would mean that space and time would go on forever and see no end. Sounds relatively reasonable right? That is, until ‘you’ decide to take a journey out into the universe and document what you would observe. As you are traveling across the universe consider that there is a set amount of combinations and permutations in which matter can reorganize itself. Meaning that, matter can only reorganize itself so much before it starts forming duplicates. Consequently, the more you travel outwards, the more familiar the universe may appear to the point where you could potentially see duplicates of the Earth and all of its components, including 'you'.

REFERENCES:

Note: A big thanks to @steemstem for providing fun and educational content relating to Science, Technology, Engineering and Math!