Hi and welcome. Today I will continue my discussion of nonlinear dynamical systems and the chaos theory. I hope you will find it worthwhile. I have been writing posts in relations to my PhD research work for the past one month. Recently I took a detour to talk about the tools I am exploring for use in my analysis. I am investigating the nonlinear behavior of ionosphere during solar eclipse. I am writing updates on what I read about. Why am I doing this? Well for two primary reasons which are not really far-fetched.
Firstly, I realized a long time ago that if you claim to have learnt something, but you cannot write it down, or explain it to others to learn also, then you have not learnt. Secondly, by writing whatever I am doing/reading in my own way, it will best serve my memory in retaining the knowledge. Any other reason you might think of is actually secondary to me. It’s like the icing on the cake.
Let us begin right? Before I go too far, I will like to make a quick distinction between real and ideal systems. Since I will also be talking about models. I’m sure you hear of real systems and ideal systems, and you might be wondering what the difference between the two is really. Well, I want to tell you that ideal systems really do not exist. That is why idealizations are called models. Models are predictions of how real physical process should behave. The main aim of models is to capture the features and behavior of real-world processes.
Models depict perfects systems. Systems that conform to all the theoretical predicted behavior. Well I don’t know any of such system. However, what I know exist in the vast universe are real systems. When real systems are approximated, they become an ideal system. Nature itself is an approximation of the ideal. For example, the ideal gas equation represents how an ideal gas is expected to behave, sorry to disappoint you by telling you that what we have are real gases. I am making this clarification because of the physical systems we deal with. Of course I am a physical scientist, and I deal with real systems. At best, some simplifications have to be made for the systems to be an approximation of what is predicted by the models. Therefore, the model either captures the behavior due to its simplicity, or the systems behavior conforms to the model by its simplification.

[image:Kalman filtering (prediction and update) credits: Wikimedia commons under the Creative Commons CC0 1.0 Universal Public Doamin Dedication]
In my last post I talked about dynamical systems being of two types. They are linear and of course nonlinear dynamical systems. Of particular interest are nonlinear systems which I will be dwelling on here.
As a reminder also, nonlinear systems can be periodic, quasiperiodic, chaotic and hyperchaotic. I think it is good for us to know when a system can be classified into any of these groups. Of course, a major characteristic of nonlinear dynamical system is their sensitivity to initial conditions. So, all nonlinear dynamical systems show sensitive dependence on initial conditions.
Generally, a periodic system or quasiperiodic system must have the following properties:
- At least one nonlinear factor (term) must be present in the system
- It must be at least one dimensional
One major quantifier used in determining where a dynamical system belongs in these four categories is the Lyapunov exponent. Nonlinear dynamical systems are said to be periodic if the Lyapunov exponent is negative. Also, the number of the attractors has to be countable. For quasiperiodic systems, Lyapunov exponent will be zero.
What of chaotic and hyperchaotic system?
For chaotic systems, there must be at least one nonlinear term in the system, it must be at least two dimensional, and the system must also have at least one positive Lyapunov exponent.
Hyperchaoticity demands that the systems have at least one nonlinear term as well, but in terms of dimension, it must be at least four dimensional, and the system must have at least one positive Lyapunov exponent.
Okay, Lyapunov exponent all the way. I have just been making a distinction between nonlinear dynamical systems on the grounds of their Lyapunov exponent. Let me explain that now.

[image credits: Wikimedia commons under the Creative Commons CC0 1.0 Universal Public Domain Dedication] 𝛌 in the equation written on the right bottom corner is the Lyapunov exponent.
The Lyapunov exponent also called the Lyapunov Characteristics Exponent (LCE) is named after Aleksandr Lyapunov. It describes the rate at which the system diverges for a change in the initial conditions. i. e. it quantifies the rate at which close trajectories or path of a system are separated for different initial conditions.
Consider it this way, different initial conditions of a system will follow different trajectory of evolution in time. If two very close trajectories are considered, the Lyapunov exponent is what quantifies the rate of divergence. The rate of this separation can be different for different configurations of initial separation vectors. What this mean is that there would be several of such Lyapunov exponent. The number of Lyapunov exponent of a systems depends on the system's dimension in state (phase) space. However, one of the Lyapunov exponents will be zero since there won't be divergence for a perturbed path in the direction of the unperturbed path. The maximum one is often referred to as the Maximal Lyapunov Exponent. The larger the value of the Maximal Lyapunov exponent, the more the divergence. I will talk more of the Lyapunov exponent in fine details in my other post on the subject matter. For now, I will maintain my trajectory on chaos theory.

[image credits: Pixabay CC0 Creative Commons]
Chaotic behavior are being exhibited by many physical systems such as weather and climate and many other physical systems, some of which I highlighted in my previous post.
Chaotic behavior of systems is being studied with the use of mathematical models and various analytical techniques. These includes phase space methods, Approximate entropy (ApEn), Sample Entropy (SampEn), False Nearest Neighbors, Recurrence plot etc. I will discuss some of these techniques in my subsequent post.
The high sensitivity of chaotic system to initial condition is often referred to as the butterfly effect. Although the phrase “butterfly effect” has been used in many instances, to imply cause and effects, the location of the aforementioned have varied widely. One notable use was in 1972 when Edward Lorentz presented a talk at the 139th gathering of the American Association for the Advancement of Science in Washington, D.C titled:
Predictability: Does the Flap of a Butterfly’s wing in Brazil set off a Tornado in Texas?[1]
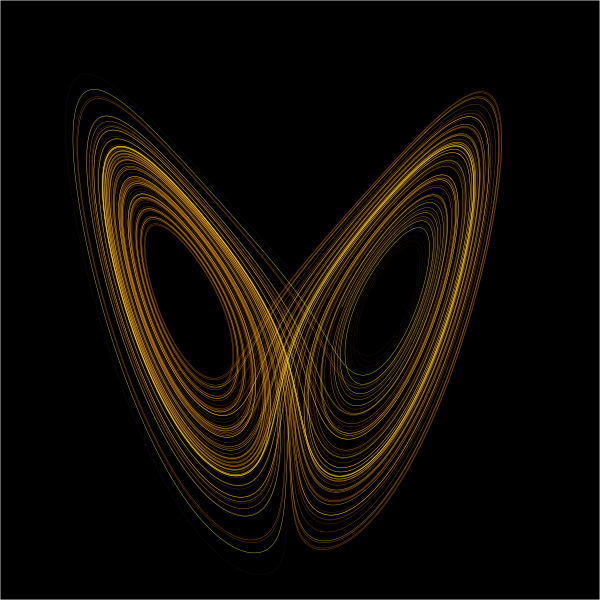
[image credits: Wikimedia Commons under the Creative Commons Attribution-Share Alike 3.0 Unported License ]
Well in actual sense, you might want to explore the possibility of this happening. For a change in weather to occur, there must be fluctuations in air pressure which is achieved when a butterfly flapped its wings. But how plausible will the effect of that be on the occurrence of tornado in Texas? Well, the fluctuation in air pressure generated by the butterfly dies off a few inches away.
Needless to say, the butterfly effect is just a metaphorical statement to illustrate the effects small changes in initial conditions will have on a chaotic system. In the case of the weather forecast from which the butterfly effect originated, some researcher have debunked the plausibility of this on the challenges of accurate predictions over long period of time. However, many believe that other factors such as individual/ location of clouds poses a big limitation in weather models, as these factors hinders the establishment of a perfect model.[2]
Summary
Chaos theory has become a fascinating field of study in contemporary science. Although it will not be wise to hide under this theory in explaining changes or difficulties in predictability of further future state of a system unless one has rigorously investigated and found that the conditions for chaos are met. The better understanding of chaotic behavior of systems will lead to better formation of models and help in further closing the gap between real systems and ideal systems.
On the butterfly effect, it will be well appropriate to know that although the input of butterfly wing-flapping scale changes into the existing weather models might not necessarily cause it to diverge, but a collection of these small changes could make a significant effect.
References:
Holger Kanz and Thomas Schreiber:Nonlinear Time Series Analysis.Second Edition. Cambridge University Press. ISBN 0-521-52902-6
CHAOS: Introduction to Dynamical systems. Kathleen T. Alligood, Tim D. Sauer, James A. Yorke. Springer: ISBN 0-387-94677-2
Thanks for all the efforts you put in this post. Very informative.
A confusion many people have is that they associate chaotic systems with random systems.
This is wrong of course.
The word chaos may not have been the best chosen for this theory.
You are right. Chaotic systems differs from random systems both in properties and behavior.
Thanks for your usual comment.
So what does linear factor mean in the sentence** one linear factor must be present in the system**
As a note on chaos. There is no universal definition of chaos. Furthermore, there are many non-equivalent definitions of chaos. The definition for chaotic dynamics using Lyapunov exponents is just one of many.
This statement all dynamical systems show sensitive dependence on initial conditions is not true
Thank you @mathowl for the correction. As you might have noted, I was talking about nonlinear dynamical system even from the sub-heading. I must have unconsciously omitted the word "nonlinear" when stating that.
I just realized I kept saying linear as against nonlinear that I am discussing. Quite disheartening. Imagine the word document for this post I wrote some months back has nonlinear all through. I have made the corrections. You can peruse now and let me know what you think.
Yes. Lyapunov exponent is one of many. I recently had a discussion with some who worked on chaos and has never used the Lyapunov exponent.
Thanks once again!
Good job in correcting it.
I am still not sure what you mean with nonlinear factor. A linear and a nonlinear system can both exhibit periodic behaviour. In the linear case just consider the discrete dynamical system with phase space \mathbb{R} / \mathbb{Z} and evolution operator x \mapsto a x where a is a real non-zero constant. The evolution operator is linear and it exhibits periodic behaviour.
You are right; a periodic system can be linear or nonlinear. With nonlinear term, I am referring to the function that specifies the change in the system. That is, the rule governing the system must contain nonlinear term.
So sorry for my belated response, I have to teach kids in a rural community every day where we hardly get internet connection. I only see comments and read post when I get home around this time.
so then the following statement does not make any sense:
I really don't understand what you mean. Are you implying that a nonlinear dynamical system cannot be periodic or quasiperiodic? because then what I have been reading in various text will be false.
What I am saying in a nutshell is that the equation of motion for nonlinear systems will have at least one term that is either a square or higher power, a product of two or more variables of the system or even a more complicated function etc.
1)Could you maybe specify why you think I am implying that a nonlinear dynamical system cannot be periodic or quasiperiodic?
2)You said
In the post you said
These statements seem to contradict. Or the use of generally in this sentence is strange.
3)the statement that all nonlinear dynamical systems show sensitive dependence on initial conditions is not true. (I thought you corrected it differently)