Do opposites really attract? Do first impressions count? You won't believe me but there actually exists a mathematical model for love which can answer these! The idea was first conceived by Strogatz in 1988. Let's see what it was.

Source:Pixabay.com
Let's begin by defining the mathematical quantities for our characters Romeo and Juliet:
- R(t) is Romeo’s love for Juliet at time t with positive value meaning love and negative meaning hate.
- Similarly, J(t) is Juliet’s love for Romeo.
- a and b determine Romeo's romantic style(you will know what it means in a moment).
- c and d determine Juliet's romantic style.
The general equations relating them being:
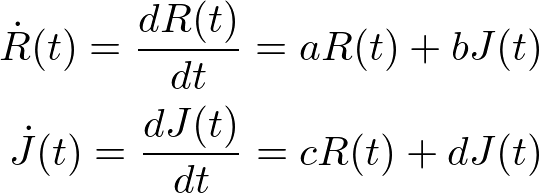
A positive value for Rdot(t) would mean that R(t) increases with time. Similarly, a negative value would mean R(t) decreases with time.
You might be wondering how do we find the value of a, b, c and d. We don't actually need the values of a, b, c and d. Just the sign of the coefficients i.e. the coefficient is positive or negative is enough. As you can see, a positive value for a would mean that Romeo is encouraged by his own feelings, while a negative value would mean the opposite. Similarly, for b, a positive value of b would mean that Romeo is encouraged by Juliet's feelings while a negative would mean that he is discouraged by Juliet's feelings.
Now let's talk about what Strogatz meant by romantic styles. He and his students came up with the following:
- Eager beaver: a > 0, b > 0 (Romeo is encouraged by his own feelings as well as Juliet’s.)
- Narcissistic nerd: a > 0, b < 0 (Romeo wants more of what he feels but retreats from Juliet’s feelings.)
- Cautious (or secure) lover: a < 0, b > 0 (Romeo retreats from his own feelings but is encouraged by Juliet’s.)
- Hermit: a < 0, b < 0 (Romeo retreats from his own feelings as well as Juliet’s.)
Cautious lovers are the most common type of people.
Juliet can be classified in the exact same way, with a corresponding to d and b corresponding to c.
I will not be solving the equations to avoid making the post too technical, but if you are interested you can read here how to solve a pair of coupled linear differential equations. You can also try Wolfram Alpha to solve and plot the equations online.
Results
Now let's jump into the results:
Fire and Ice
If two people are exact opposite, then c= - b and a= - d. This is possible for two combinations:
Eager beaver and Hermit
Now the outcome depends on whether they give priority to themselves or to the other i.e. |a|>|b| or |a|<|b|.
For the case with more priority given to one's own feelings, |a|>|b|, we get:
source:self
Which means that they end up in odds, or one loves but the other hates. The arrows show the direction over the contour in which the relationship moves with time.
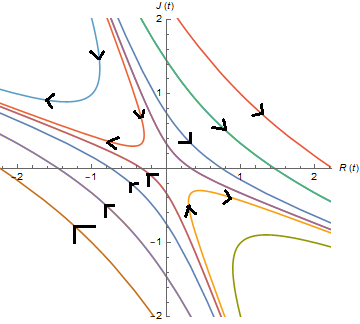
For the case where they give their other half's feeling more importance, over there own, |a|<|b|, we get:
source:self
Which means that there is an endless cycle of hate and love with about a quarter of the time of mutual love and a quarter of mutual hate.Narcissistic nerd and cautious lover:
Again, the outcome depends on whether they give priority to themselves or to the other i.e. |a|>|b| or |a|<|b|.
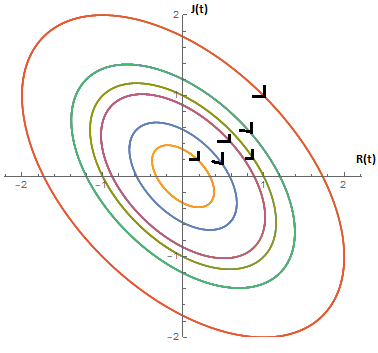
For the case with more priority given to one's own feelings, |a|>|b|, we get:
source: self
which means that the couple either end up deep in love or in an all-out war!
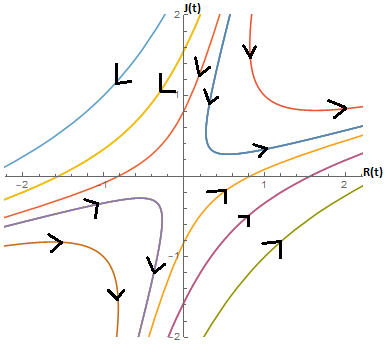
For the case where they give their other half's feeling more importance, over there own, |a|<|b|, we get:
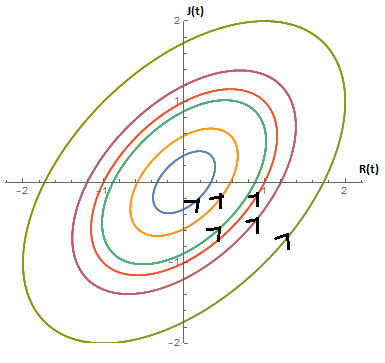
source: self
We again get an endless cycle of love and hatred.
So "opposites attract" but more often than not end up hating each other.
Out of touch with one's feelings
Suppose both Romeo and Juliet are out of touch with their own feelings (a = d = 0) and only responding to the other.
Then three cases are possible.
- Two lovers: b > 0, c > 0. This gives similar results as a narcissistic nerd and a cautious lover with |a|>|b| i.e. mutual love or hate.

source: self
- Two nerds: b < 0, c < 0. This gives results similar to Eager beaver and Hermit with |a|>|b| i.e. one loving and the other hating..

source: self
- Nerd and lover: bc < 0. This again gives a center like earlier:

source: self
As you can notice the initial condition or the first impressions matter a lot in most cases. "First impressions" are actually very important!
Next time your friend or you get a partner, try predicting using these equations and be the three-eyed raven!
References
- Strogatz, Steven H. "Love affairs and differential equations." Mathematics Magazine 61.1 (1988): 35.
- Sprott, J. C. "Dynamical models of love." Nonlinear dynamics, psychology, and life sciences 8.3 (2004): 303-314.
Found the post interesting?
Can you tell, how to shout a secret message to a stranger in public and understand each other while that nobody else has a clue? Here's how you can!
Read about how clocks and Mathematics are closely related in my previous post: Clocks and Mathematics
Follow me at @omstavan for more such posts!
Hi! I am a robot. I just upvoted you! I found similar content that readers might be interested in:
http://sprott.physics.wisc.edu/pubs/paper277.pdf
Yup, this is the 2nd paper in the references!
@originalworks
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
img credz: pixabay.com
Nice, you got a 92.0% @tard upgoat, thanks to @omstavan
Want a boost? Minnowbooster's got your back!
Congratulations @omstavan! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPCongratulations @omstavan! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOP