Disclaimer: I lay no claim to the originality of the basic ideas expounded here. Its distinctness lies more in its scope and in the detail of its exposition.
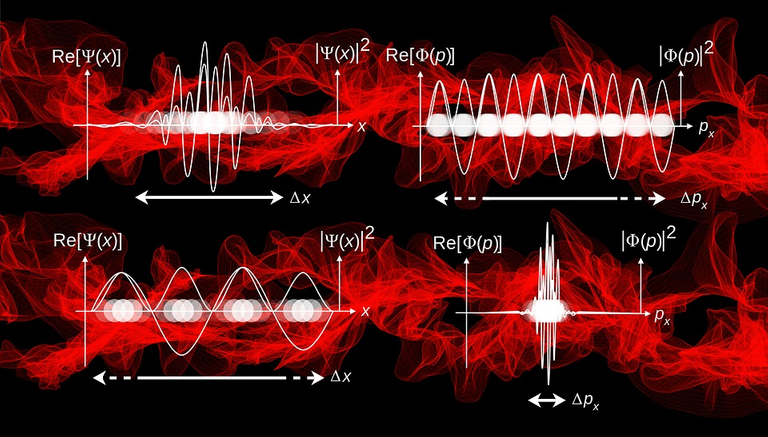probabilistic interpretation of wave function CC0 Creative Commons
Probabilistic Interpretation:
As in any field of study, a particular system has an associated state. In quantum mechanics, the state of a system of particles over a space at a particular time is best described by what is known as the wave function. Conventionally written as,
The content of the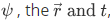 
, is its dependence, such that the wave function changes if we change 
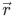and/or t.
The jargon "wave function" is not an ordinary kind of function we met in calculus. Though it has some properties we've already encountered. For instance, a wave function has to be differentiable or smooth. In addition a wave function is a complex function, and by that I mean that it is not a value we can associate to the physical world. We have to do something about this wave function in order to obtain a value we can put into some kind of experiment.
Note, however, that by knowing the wave function, we can make some precise predictions of the probability of the various possible outcome of any given type of physical measurement on the particle. In particular, in a position measurement, the probability of finding the particle within some volume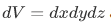 
at time t is
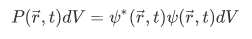
Here we introduced the complex conjugate of the wave function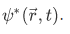 
In some other standard, the equation above is written as,
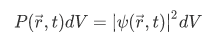
If you're familiar with probability theory, it is easy to see that the function 
has to have a dimension of 
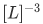if we want the left to imply as a measure of probability.
We can also say that the wave function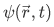 
is the probability amplitude and must have a dimension of 
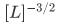for consistency.
If we take the integral of the equation we have from in all space, we know that we must find the particle somewhere hence a probability of one,
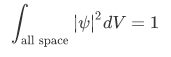
If the wave function has this property, it is said to be normalized. By normalized, we mean that total summation or integration must be equal to unity. If we don't have a normalized wave, we obtain an integration that is not unity. Note, however that we can normalized all wave function as long as it is integrable.
Definite Energy and Definite Momentum
Lets say we have a system of state of definite energy E, (by definite we mean a non-fluctuating E). And lets assume we can express our wave function as a product of separate variables, that is:
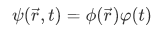
The time dependent factor is given by
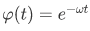, where 
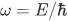such that 
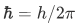in which 
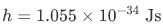is the planks constant.
Another way to express the time-dependence of the wave function is given by,
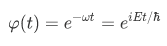
Note that this is always the form of the wave function's time dependence if we have a system of definite energy E.
How about a system of definite momentum?
If we have a system of definite momentum, the space dependent part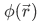 
of the wave function is a harmonic wave, by harmonic wave we mean that
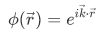
where 
is related to the momentum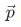 
by the de Broglie relation
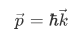
and we can extract various information by exfoliating the equation above,
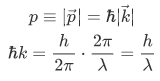
The 
is the wavelength associated with the wave number k. From this information we can actually express the wave function of a particle with definite momentum as a plane wave,
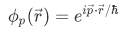
We now have the form of our separated function of the wave function. We can put them together to obtain a more descriptive equation of its motion,
The last equation can be visualized as a moving wave. Or in other words, a wave function is actually a wave front that moves along the direction of the momentum p.
Interfering Electron Wave Packets animated Wikimedia Commons
Credit
- all equations are generated using Sharelatex
- the first image is obtain from Pixabay under CC0 Creative Commons
- the last image is obtain from wikipedia
You got a 4.74% upvote from @minnowvotes courtesy of @pauldirac!