
This is the fifth in my series of killing time at work using math (here are the others 1, 2, 3 and 4).
If you have read my posts before you already know that there are a few prerequisites for this:
- You like recreational math.
- You work at a computer and have access to Microsoft Excel.
- You are bored out of your tree.
- You don't want to get caught slacking off.
Let's get started.
In this post I am going to calculate the sunset and sunrise times for Toronto, Canada on April 16 2018.
To make it work for your location, just replace the latitude and longitude with that for your location and revise the date. Remember longitude W is negative and longitude E is positive.
This was quite a tricky calculation and it actually took me a bit of work to get this calculation right so for the moment so I am not sure if this is a perfectly general calculation yet.
This post used the system of equations that are described on this Wikipedia page: Sunrise Equation.
If you are going to do this yourself it would be best to have this page open and to translate it into your spreadsheet from there.
Note that the trickiest part of this spreadsheet is keeping degrees and radians separated. The equations in the Wikipedia page use degrees but Excel uses radians when calculating trigonometric functions. So be careful.
It's a fairly large spreadsheet so I am going to provide it in 2 segments.
Citations notice:
- All spreadsheet images in this post are my own work.
- All equation images in this post are taken from this Wikipedia page: Sunrise Equation.
Segment #1

Cell C2 is the latitude of Toronto and is 43.6 degrees N. Here you would input your own latitude.
Cell C3 is also the latitude of Toronto but this time it is in radians. To get radians multiply by 2π and divide by 360° to get 0.7609
Cell C4 is the longitude of Toronto which is 79.4 degrees W. In the system of equations W is negative and east is positive. Here you would input your own longitude taking care of the east/west sign.
Cell C7 is the Julian date for January 1 2000 at noon. Astronomical calculations use something called Julian Date which is the number of days since Monday, January 1, 4713 BC. The Julian date of January 1 2000 at noon Greenwich meantime is 2451545.
Note: Julian dates are weird in that they start at noon. I guess astronomers stay up all night and don't want their dates changing while their telescopes are out?
Cell C8 is the same date but in normal Western calendar mode.
Cell C9 is the current date at Greenwich England in normal Western calendar mode. I set the time in this field to midnight (i.e. 12:00:01 AM) and not to noon (12:00:00 PM) as you might do if you were tempted to emulate a the Julian date protocol of starting the day at noon.
Cell C11 is the number of days since "JD2000" (Julian date 2000). This is just cell C9 - C8 and comes out to 6680 days.
Cell C12 calculates the current Julian data and is cell C7 + C11. I get 2458225 for April 16 2018 at noon.
Validation: I validated this calculation using this website: U.S. Naval Observatory Julian Date Convertor which gave me the same answer for for April 16 2018 at noon.
Cell C13 is the first calculation from the Wikipedia page and calculate the Julian date with an adjustment for leap seconds.
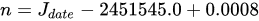
In Excel this is:
=C12-2451545+0.0008 = 6680.0008
Cell C15 is called J* (J-star) and calculates mean solar noon and used 'n' from above and the longitude divided by 360.
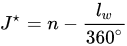
In Excel this is:
=C13-C4/360 = 6680.221356
Cell C16 is M and estimates the solar mean anomaly. It uses J* and calculates the modulus 360 of the equation below.

In Excel this is:
=MOD(357.5291+0.98560028*C15,360)
Cell C17 is M but converted to radians. The Wikipedia page uses degrees in the equations but Excel uses radians when calculating sines and cosines so you need to be careful to keep them straight.
Cell C18 is C and is called the equation of center. It is calculated according to this equation:

In Excel this is:
=1.9148*SIN(C17)+0.02*SIN(2*C17)+0.0003*SIN(3*C17)
As I said in cell C17, it is important to keep the degrees and radians carefully sorted out since Excel calculates trig using radians.
Cell C19 is called Lambda, it calculates the ecliptic longitude wit this modulus 360 equation:

In Excel this is:
=MOD(C16+C18+180+102.9372,360)
Cell C20 is Lambda again but converted to radians.
Cell C21 is called Jtransit ("J-transit"), and it calculates the solar transit using this equation:
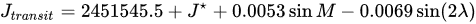
In Excel this is:
=2451545.5+C15+0.0053*SIN(C17)-0.0069*SIN(2*C20)
Segment #2
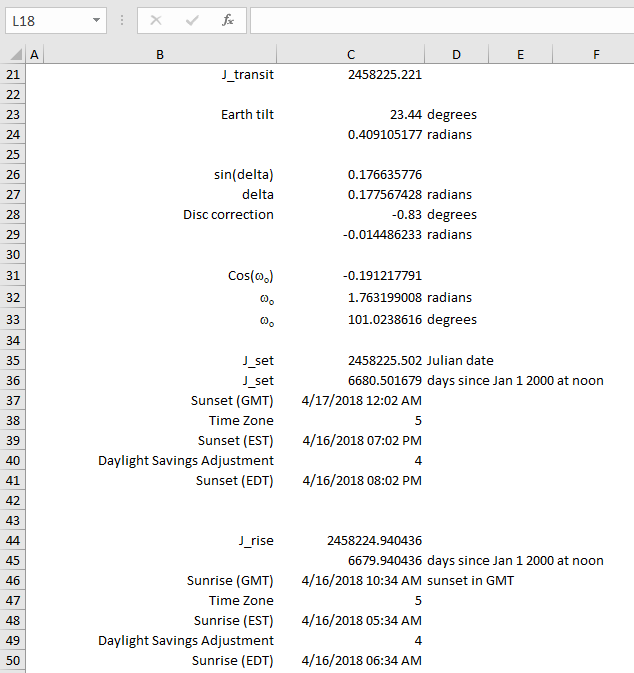
Cell C23 is the tilt of the Earth's axis and it 23.44°.
Cell C24 is the tilt of the Earth's axis converted to radians.
Cell C26 is the sine of delta the inclination of the Sun ( sin(δ) ) and is calculated using to this equation:

In Excel this is:
=SIN(C20)*SIN(C24)
Cell C27 is the angle delta and is calculated as
In Excel this is:
=ASIN(C26)
Cell C28 is the Sun's disc correction of -0.83°C
Cell C29 is the Sun's disc correction in radians.
Cell C31 is called the hour angle, it calculated cos(ω0) as:
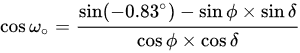
In Excel this is:
=(SIN(C29)-SIN(C3)*SIN(C27))/((COS(C3)*COS(C27)))
Cell C32 calculates ω0 using
In Excel this is:
=ACOS(C31)
Cell C33 converts ω0 from radians to degrees using
In Excel this is:
=360*C32/(2*PI())
Calculating Sunset and Sunrise
Now we are finally at the point where we can calculate the times of sunset and sunrise.
Cell C35 is called Jset as
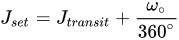
In Excel this is:
=C21+C33/360
This gives me the Julian date of sunset at Toronto which is the time recorded by clocks in Greenwich England. I need to figure out the date and time in Toronto.
Cell C36 gives me the number of days since January 1 2000 at noon.
In Excel this is:
=C35-C7
Cell C37 adds the number of days from C36 to the date in Cell C8. This gives me the time of sunset in Toronto but in the time recorded by clocks in Greenwich England.
In Excel this is:
=C8+C36
Cell C38 is the time zone for Toronto. Toronto is 5 time zones west of Greenwich England so we need to subtract off 5 hours. If you live east of Greenwich then you need to add your timezone hours.
Cell C39 is the result of subtracting off those 5 hours but we are not done yet because Toronto is currently in Daylight Savings Time which adjusts the clocks ahead by an hour.
Cell C40 adjusts for Daylight Savings Time by setting the decrement to 4.
The Answers
Cell C41 gives me the final result of this long calculation: 8:02 PM.
Doing similar calculations for sunrise:
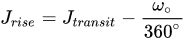
and I get 6:34 AM.
Validation
Going to Google Search I typed in "sunset Toronto April 16 2018" and got 8:02 PM which is the same answer.
For sunrise Google gives me 6:33 AM which is a very close answer.
Closing Words
This was a very tricky calculation but it is well worth doing if you are into astronomy.
This calculation is specific for Toronto, Canada and for April 16 2018 but I think all it takes is for you to plug in your latitude, longitude, time zone and the date to get the sunset and sunrise times for your location.
I have checked it against other cities (Tokyo Japan, Perth Australia, Moscow Russia) and other dates in the year and it seems to be a robust calculation.
Thank you for reading my post.
Post Sources
- All spreadsheet images in this post are my own work.
- All equation images in this post are taken from this Wikipedia page: Sunrise Equation.
- Wikipedia Sunrise Equation page: https://en.wikipedia.org/wiki/Sunrise_equation
That's interesting that you had to adjust your JD by 0.5 day. That means your M could be off as well, but the error of 0.5 of a day in that calculation would only amount to about 2 minutes difference in sunset and sunrise.
Thanks. I found the problem: I had originally set the Western calendar date in cell C9 to start at 12 noon in order to emulate the Julian calendar pattern of starting the day at noon. I should not have done that.
The equation in cell C21 for J_transit also does this. I guess the person developing the system of equations was already compensating for this.
So there was a double compensation for the Julian calendar quirkiness of starting the day at noon which gave me the error of being off by 12 hours.
I have now adjusted cell C9 to start at midnight (12:00:01 am) and set cell C21 back to the form of the equation in Wikipedia and everything works.
Wow.. This is amazing.
How did you use latex. I have been looking forward to getting some equations on steemit.
In this case I simply copied over the Wikipedia equations and made sure that I cited the source.
In other posts I used the Codecogs latex editor: https://www.codecogs.com/latex/eqneditor.php which works very well.
Thank you for your help.. I would try this.
Let me know how you do. I found it to be a very tricky calculation that why I posted my advice here.
I know some algebra. I am not sure if I can keep up with calculus but I appreciate the value of calculating, formulating. Thanks for sharing. I'm Oatmeal.