This is the third in my series of killing time at work using math (here is the first and the second).
As before, there are a few prerequisites for this post:
- You like recreational math.
- You work at a computer and have access to Microsoft Excel.
- You are bored out of your tree.
- You don't want to get caught slacking off.
If a butterfly flaps its wings in Japan a city is destroyed in Kansas two weeks later. Why do Japanese butterflies hate Kansas so much?
To an average person chaos means random and a chaotic system would seem to them to be something that simply behaves in a lawless anarchic manner.
To a mathematician or a physicist though chaos means a dynamic system that is highly sensitive to initial conditions.
If you start off with a weather pattern and simulate it in a computer to predict 2 weeks into the future you get an answer, maybe it says that it will be sunny weather in Manhattan.
Start off again with the same weather pattern but change the wind speeds by maybe 1% and the answer you now get is a thunderstorm in Manhattan in 2 weeks.
Systems like these are called mathematically chaotic and in this technical sense it does not mean random, it just means very sensitive.
A Simple Chaotic System
The simplest chaotic system is described by the process:
In words: you just take any value of x that is between 0 and 1 and run it through the above equation to calculate a new x. Then you take that new x and run it through the same equation again to get another new x.
Keep iterating and plot out the answer. It is surprising what you get.
Let's start.
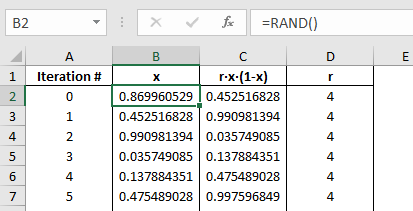
In the first column (column A) I just set up a simple count of the iterations, 1, 2, 3, 4, and so on.
In the first cell of the second column (cell B2) I just set up a random function.
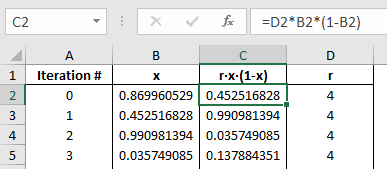
In the third column (column C) I set up the equation 4·x(1-x) where x is the value in to its left in column B.
The value of 'r' is put into column D, I do this for a reason that I will explain later.
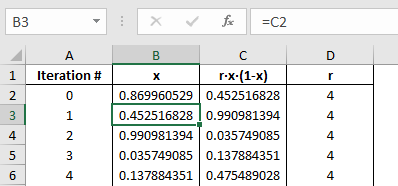
In the remaining cells of the second column (column B) I just make them equal to the answer I get from the above equation. This sets up the iteration as you copy the rows down the spreadsheet. I did this for 1000 rows.
Okay, let's plot the iteration number on the x-axis and the value for x on the y-axis and see what we get:
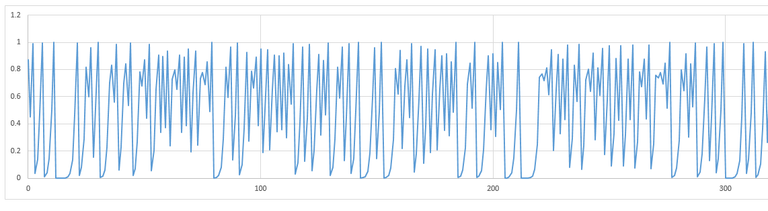
Interesting, from that seemingly simple equation we get some pretty chaotic behaviour. It is not random because if you started from the same value of x you will always get the same sequence of subsequent values.
Okay, let set the value of 'r' to 2.8 and see what we get.
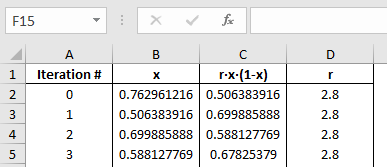
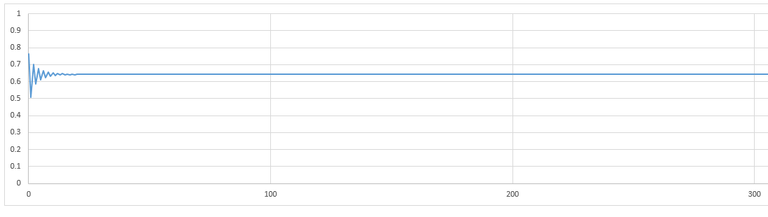
Weird. It just collapses down to one value after only a few iterations. In this case the system is not chaotic, it is nice and stable.
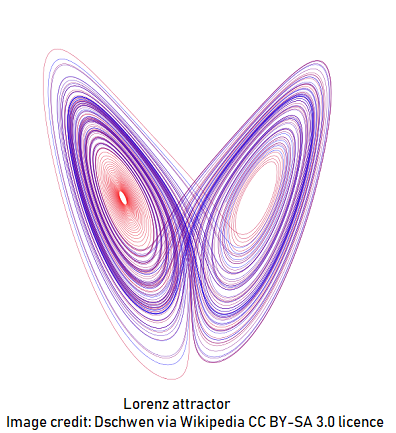
One can plot out the behaviour of the system as a function of this value of 'r' and you can kill a lot of time plugging in different values for r. In fact is has been done it is called a bifurcation map and it looks like this:
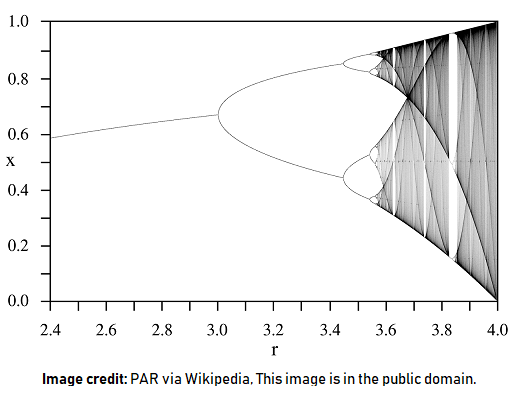
We see at a glance that there are islands of stability and areas of extreme chaos. As r increases, the system goes from single value stable, to 2 value stable (a 'bifurcation), to 4 value stable (another bifurcation), to chaos. Then it stabilizes again and goes back into chaos not too much farther along.
Creating Our Own Bifurcation Map
The bifurcation map above was no doubt created via some program but I am sure, that with just a few modifications, we can do something similar in our Excel spreadsheet.
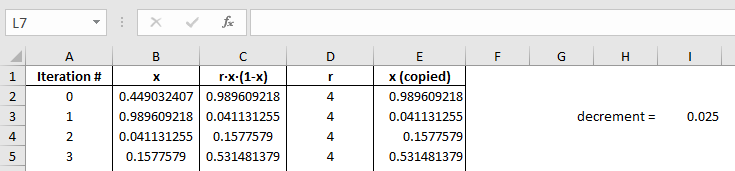
The revised spreadsheet is basically the same except for three easy differences:
- I created a decrement value in cell I3 and set it to 0.025. More about that later.
- I copied the x value over into column E (called 'x copied'). This just makes it easier for me to create the graph.
- Starting at iteration 1001, I decrement the 'r' value by 0.025 as shown here:
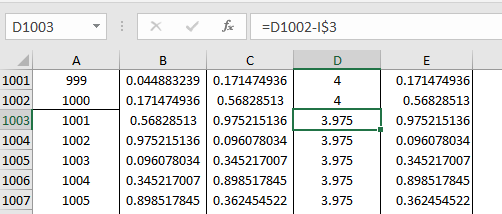
I do this decrement operation every 1000 iterations until r drops down to a value of 2.4.
Let's see what we get in the plot of 'r' versus 'x' (column D versus column E):
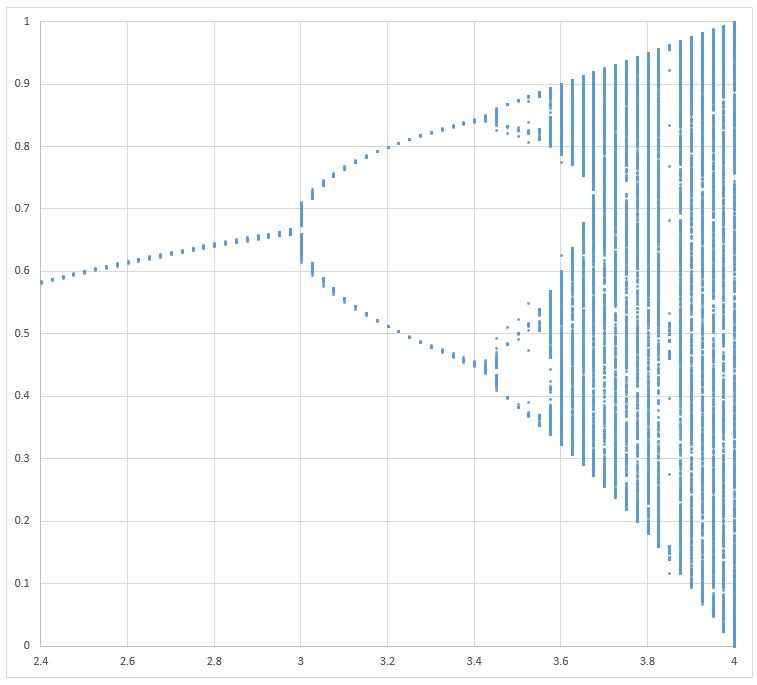
Not bad. That's 65,000 points and it almost brought my poor old computer to it knees but I think that it is pretty close to the computer plot above from Wikipedia.
Closing Words
Chaotic systems and strange attractors are a fascinating area of math. I may do a future post on what they mean and how they are used.
I hope that this was interesting and enabled you to kill some time at work without looking like you were slacking off.

Thank you for reading my post.
SWEET! Once I noticed the photo of the Lorenz attractor I automatically knew you were getting into chaos. Dabbled in the concept myself years ago. Its a fascinating area of math. You have some really good spreadsheet skills there. What do you think these islands of stability mean in a chaotic concept?
I think I will get into that in a later post. I have ideas but I don't want to spoil the next post.
Really looking forward to that one. Great subject!
I smell a heavy dose of future non-linear dynamics articles. Will wait for those. :)
I've a better alternative for your "Chaotic systems and strange attractors"... I challenge you to co-write an article with me on the Lorentz transformation! I'm stuck with the writer's word-beat, you have the knowledge I'll never have but will always question... And, hey, I have a peculiar humor! Read this with those girlfriends in mind: "a bifurcation diagram shows the values visited or approached asymptotically—fixed points, periodic orbits, or chaotic attractors..." If you "can plot out the behaviour of the system as a function of this value of 'r',"→ {web☺me422.us} ! ∜mp