Hello friends of steemit, today we continue talking about semiconductors. On this occasion we will talk about electrical resistivity.
You can see the first part here

Source
The current density due to gaps (e) and electrons (-e) is equal to the product of their respective charge density and velocities. Therefore, the current density or the charge density per unit time transported by gaps and electrons is:
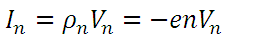 (1)
(1)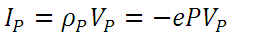 ( 2)
( 2)Where  refer to the charge densities associated with electrons and holes (
refer to the charge densities associated with electrons and holes (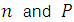 ).
). 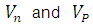 are the average vector velocities of the electrons and holes respectively.
are the average vector velocities of the electrons and holes respectively.
Since the average electronic speed is 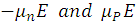 for electrons and holes, where
for electrons and holes, where 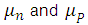 are the mobilities of the electron and the gap, and E the electric field; Equations (1) and (2) can be written as follows:
are the mobilities of the electron and the gap, and E the electric field; Equations (1) and (2) can be written as follows:
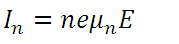 (3)
(3)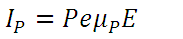 (4)
(4)Then, the total density of electric current I can be expressed as:
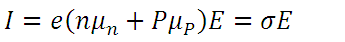 (5)
(5)Where the electrical conductivity σ is given by:
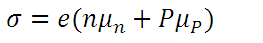 (6)
(6)Then, the electrical resistivity (ρ) of a material is given by:
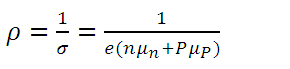 (7)
(7)Where the mobilities 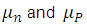 are defined as:
are defined as:
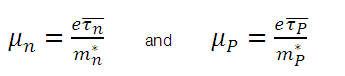 (8)
(8)Where 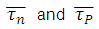 are the weighted averages of the relaxation times for electrons and holes on the Maxwell-Boltzmann distribution. The terms
are the weighted averages of the relaxation times for electrons and holes on the Maxwell-Boltzmann distribution. The terms 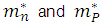 represent the effective mass of the electrons and holes respectively.
represent the effective mass of the electrons and holes respectively.
It should also be noted that 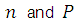 are the actual instantaneous values of the concentration of holes and electrons that are not necessarily identical to the equilibria densities of holes and electrons
are the actual instantaneous values of the concentration of holes and electrons that are not necessarily identical to the equilibria densities of holes and electrons 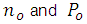 .
.
Until now it has been assumed that there are no carrier density gradients that are related to the equilibrium state, hence the following can be deduced:
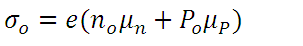 (9)
(9)Where 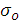 is the corresponding value of the electrical conductivity.
is the corresponding value of the electrical conductivity.
It is necessary to establish this distinction, because it is possible to create carrier densities in excess of the equilibrium values in semiconductors.
For an intrinsic semiconductor with carrier densities 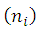 equal to the equilibrium values,
equal to the equilibrium values, 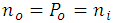 , equation (9) takes the following form:
, equation (9) takes the following form:
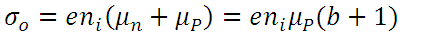 (10)
(10)Where b is defined as the relationship between the mobility of electrons and holes, ie:
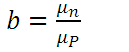 (11)
(11)For said semiconductor, its electrical resistivity is the following:
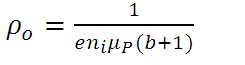 (12)
(12)If we define 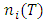 , which represents the number of holes or electrons per unit volume within an intrinsic sample of the semiconductor as a function of temperature (T), by means of the following relationship:
, which represents the number of holes or electrons per unit volume within an intrinsic sample of the semiconductor as a function of temperature (T), by means of the following relationship:
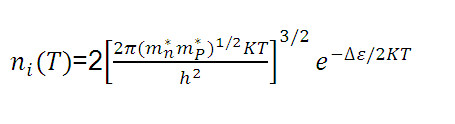 (13)
(13)where Δε is the forbidden energy gap of the semiconductor, that is, it is the energy difference between the conduction band and the valence band. 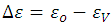 .
.
The term K is the Boltzmann constant and h represents the Plank constant.
Using equation (10), we can write equation (13) in the following way:
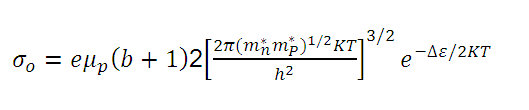 (14)
(14)Since mobility 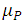 almost always has a temperature dependence that largely cancels the temperature variation
almost always has a temperature dependence that largely cancels the temperature variation  of the term preceding the exponential factor y, since b does not depend largely on temperature, the variation of
of the term preceding the exponential factor y, since b does not depend largely on temperature, the variation of 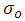 as a function of 1/T is essentially exponential.
as a function of 1/T is essentially exponential.
On the other hand, for a semiconductor that is not necessarily intrinsic, that is, extrinsic, the electrical conductivity is given by equation (9).
If we use equation (11) to eliminate 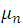 , we obtain the following equation:
, we obtain the following equation:
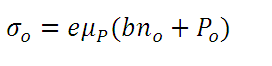 (15)
(15)Then, we use the following equations to replace 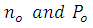
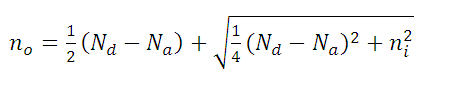 (16)
(16)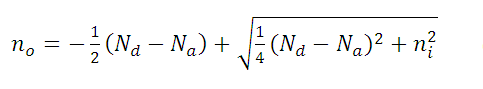 (17)
(17)Where 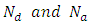 are the concentrations of donors and acceptors respectively.
are the concentrations of donors and acceptors respectively.
The electrical conductivity can be written as:
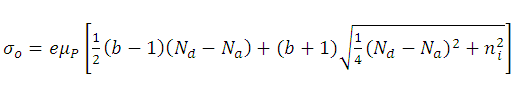 (18)
(18)Finally, the electrical resistivity of the extrinsic semiconductor is:
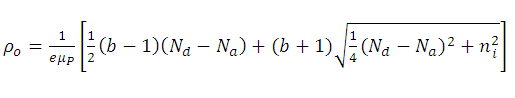 (19)
(19)REFERENCES
S.M. Sze. Physics of semiconductor devices, Weley-Interscience, second edition. 1981.
Hall, H. E. Física del estado sólido, editorial Limusa. México D.C. 1978.
Mckelvey, J. Física del estado sólido y de semiconductores. Editorial Limusa. México D.C. 1976.
Kittel, C. Introduction to solid state physics, John Willey & sons, INC. New York. 1954.
Enjoy the vote and reward!