In this little post we are going to quickly and formally prove that the function we built in Infinity and Beyond - Part 2 is in fact a bijection. This post is only for those who are really interested to see the formal proof, as we have already informally proven this in the original article.
The function
The function we created looked like this.
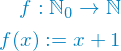
Remember that 
and 
.
Injection
Mathematical definition of injections.
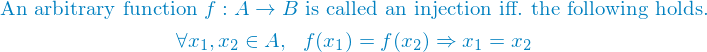
Read as "For all 
and all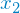 
from A, 
implies 
."
We can show this easily by starting on one side and working our way over to the other side.
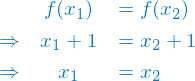
Surjection
Mathematical definition of surjections.
Read as "For all y in B there exists an x in A such that f(x) = y"
We can't show this directly, so we try to invert the function and prove that the inverted function is correct.
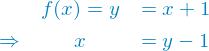
This leads to the inverse function 
. For it to be correct the following must hold.
Again, we can easily show this by working from one side to the other.
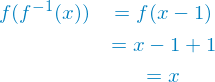
Q.E.D.
Conclusion
We just proved that our function is both an injection and a surjection, which makes it a bijection.
- Injection Definition - https://en.wikipedia.org/wiki/Injective_function
- Surjection Definition - https://en.wikipedia.org/wiki/Surjective_function
PS: The abbreviation "Q.E.D." stands for the Latin phrase "quod erat demonstrandum" and translates to "what was to be demonstrated".Source It is often found under mathematical proof. Think of it as the mathematical way of saying "The End".
Deutsche Version hier.