WARNING
This post may endanger ignorance and cause increase in knowledge! The author will not be responsible for headaches, confusion, existential crises or breakdowns of any kind. By reading this you accept that your ignorance may suffer. Read at your own risk.

Image Source
Roadmap
"Infinity and Beyond" is a series of posts about the concept of infinity, its mathematical properties and how misleading our intuition about infinity can be. It will get rather technical but I will try my best to make it as easily digestible as possible. You do not need to have studied Mathematics or a related field to understand this series.
- Part 1 - Introduction
- Part 2 - Why is Infinity plus One not larger than Infinity?
- Part 3 - Can we go bigger?
- Part 4 - Interesting Thought Experiments depending on Infinity
These are the already planned parts. This list may be subject to change.
Infinity and the Practical Applications
The concept of infinity will rarely occur in your every-day life, but it is around almost around every corner in theoretical fields like Mathematics, Physics or even Computer Science. Looking at it from a philosophical point of view, being able to think about such an abstract concept such as infinity is a sign of mankind's ingenuity and ability to abstract. After all we are yet to discover anything truly infinite.
You may argue that a circle is infinite, but only if you allow to walk over the same point multiple times. After some time you have discovered the entire circle and won't find anything new. The universe may be infinite, we don't know. However it is sufficient to think of it as finite because beyond a certain point (the fringe of the observable universe) we cannot receive any information (visual or otherwise) because the speed of light is finite. Yes, even the fastest thing in the universe and what is believed to be faster than anything, because nothing can be faster, is still finitely fast. 1
What about the small scale though you may ask. Even if you take a magical microscope there is a limit to how small things you can observe due to the uncertainty principle. Without going too much into detail here, as it could be its own article: The uncertainty principle claims that you can only measure the position and the momentum of a particle to a certain level of precision. This is because the more precise you want to measure something the higher frequency of electromagnetic radiation is needed (very quickly leaving the range of visual light). The problem is though, that the higher the frequency, the higher the energy and the higher the energy the more this particle will be influenced by the beam we use to measure it. The beam effectively bumps the particle away from the position we wanted to measure in the first place. You end up with a break even point of imprecision errors (by too low frequencies) and of error induced by the measurement (by too high frequencies).2

Image Source
At this point you may ask "Why bother at all with infinity then?". Well, in theoretical mathematics you will bump into infinity over and over again. It lets us theorize and eventually prove a whole variety of things. One essential theorem of mathematics is Gödel's Incompleteness Theorem, which states that not all conjectures that are true (or false) can be proven (or disproved). This theorem depends heavily on the fact that there are different degrees of infinity.3
Even if you aren't into the foundations of mathematics though, you may still get something out of infinity. In part 4 we will take a look at some interesting and mind bending thought experiments depending on infinity.
Wait, did you say "different degrees of infinity" just then? Is infinity not large enough? Now there are different degrees of infinity? Yes, infinity is not equal to infinity. In fact there are infinitely many infinities, each larger than its predecessors.4 But more on this in part 3.
The Foundations
Before we get to the meat of the topic though, we'll have to define some notation and make sure we are all on the same page, by quickly going through some very basics.
Set Theory
Sets in mathematics are simply unordered collections of elements or symbols where each distinct elements is only contained once in the set. We denote sets by using curly braces around the list of elements in the set. Usually capital letters will be used for naming sets. The elements may be any symbol but we will mostly use numbers for convenience. We will also need some operations on sets like union, intersection and so on. Here is an overview of the most basic notations on sets.
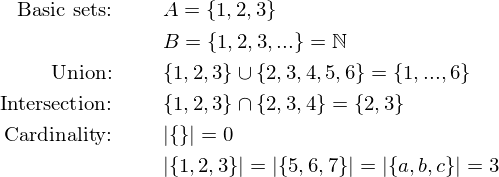
Now with the very basic notation out of the way we can start talking about infinity. Any symbols I have not yet explained I will explain when they come up.
One Example of an Infinite Set
We are all familiar with the natural numbers. Let's look at the role of infinity in the natural numbers.
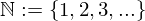
(Whether or not zero is part of the natural numbers is purely by convention and may change from paper to paper you read. We'll say it isn't.)
The set of natural numbers is the infinite set of all integer numbers from one to infinity. Or is it? This sentence is a good example for why mathematicians use those weird symbols to represent things that may as well just be explained by natural languages (like english). Because natural languages are inherently imprecise. The sentence "The set of natural numbers is the infinite set of all integer numbers from one to infinity." may be interpreted in such a way, that you might think infinity is part of the natural numbers. This is however not the case.
If you think about the intuition of natural numbers this is easily explained. The natural numbers are all numbers you use for counting. So you may start "1, 2, 3, ..." and so on. However, no matter for how long you count you will never say "infinity". You will never reach infinity, as it is not part of the natural numbers.
We now have an infinite set we are all familiar with. In the next part we will have a little play with it and see what we can do about its size.
Next Up
The next part of this post will be about why infinity plus one is not larger than infinity but rather equal. So stay tuned for one of the mind benders of mathematics.
Thank you for reading. If you have any questions or feedback feel free to leave it in the comments. I will try and answer any questions as best I can.
- Observable Universe - https://www.space.com/24073-how-big-is-the-universe.html
- Uncertainty Principle - https://www.theguardian.com/science/2013/nov/10/what-is-heisenbergs-uncertainty-principle
- Gödel's Incompleteness Theorem - https://plato.stanford.edu/entries/goedel-incompleteness/
- Degrees of Infinity - https://thatsmaths.com/2014/07/31/degrees-of-infinity
Equations created with latex2png.
Part 2 is out. Read it here.
Eine deutsche Version gibt es hier.
Congratulations @targodan! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPThis post has received a 8.26 % upvote from @whatsup thanks to: @targodan.
I don't get how there can be degrees of infinity. Infinity is surely a term to describe that which is without part or division - by its nature? I guess language, being finite, makes it a challenge!
I am glad you ask and I hope I have sparked your curiosity.
The first question we have to ask ourselves is: What do we mean by infinity? I would answer that somewhat along the lines of "Infinity is something never ending. Something that goes on forever with no end.". The problem with language and infinity is, you quickly get a recursion i. e. you can only describe infinity by using some form of the term infinity (which has a certain irony to it as it will leave you in an infinite loop of definitions).
It is now easy to think that infinite means everything which is certainly not the case. In order to not flood the comment section by a > 1000 words comment I can only give you a short example. The set of all natural numbers is smaller than the set of the real numbers (all numbers, including rational and irrational), although both are infinitely large. As a result there must be different "degrees" of infinity, or whatever term you want to use instead of degrees. The german term for this is "Mächtigkeiten" which I find particularly fitting. It roughly translates to "mightyness".
Maybe part 2 of this series can give you a better understanding of this already.
For a proper example of something larger than the set of natural numbers and proof, you'll have to wait for part 3 though.
Appreciate you attempting to give clarity. thank you.
I have been struggling to insert latex myself. I used a google api to do it, but it is not very comfortable (see at the end of this post). I will try your method, but do you know if there is any frontend for the steem blockchain more appropriate to writing math?
Not that I know of. I believe there was some discussion about steemit supporting mathjax or a simmilar JavaScript based latex compilation but it was dropped for now, as it's not trivial to do and they want to focus on core features first. Take a look at the Steemit Condenser repo, maybe you can find something in the issues.