Image credit: modified from Shutterstock
The standard Gauss-Jordan Algorithm for converting a matrix to its reduced row-echelon form is an important procedure in linear space theory. However, for computation by hand, it may lead to messy calculations involving fractions. Human beings (myself included) are prone to errors, and looking for your error is like looking for a needle in a haystack.
I think many students would want to tear their hair out doing this. To reduce frustration, I adapted the GJ algo to work with integers as much as possible, and then reduce to fractions (if necessary) only at the very last step.
Instead of writing the modified algorithm in pseudocode, which is rather abstract, I shall demonstrate with the above example to llustrate how it works. Start with the given matrix.
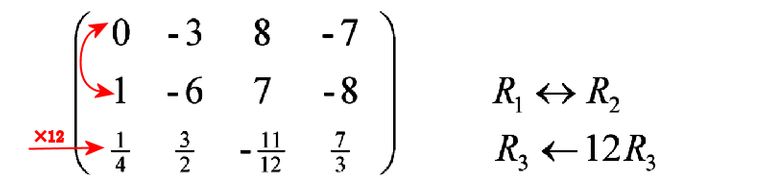
I know “1” will be a nice pivot for column 1, so let us swap rows 1 and 2. To get rid of fractions, we multiply row 3 through by the Lowest Common Multiple (LCM) of the denominators (viz. 12). This is what we get.
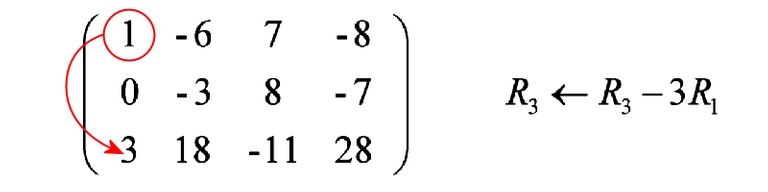
Now we have all integers. We use the “1” in column 1 as a pivot element to “attack” i.e. eliminate the “3” in that column. To do that, we subtract 3 times of row 1 from row 3.
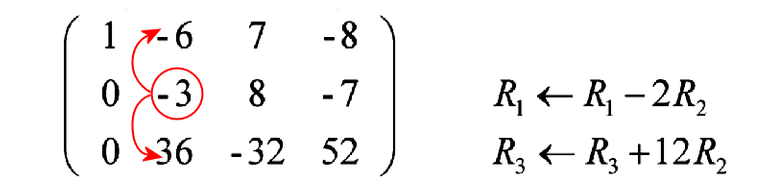
With column 1 clear, now we look at column 2 and row 2, i.e. the “-3” element. In the standard Gauss-Jordan procedure, we would divide the whole row 2 by -3, but that would lead to fractions, and later more fractions. I hate fractions! I do not want do that. However, I would still use “-3” as a pivot element to “attack” i.e. clear away the other elements in the same column. Subtract twice of row 2 from row 1 and add 12 times of row 2 to row 3. This is what we get.
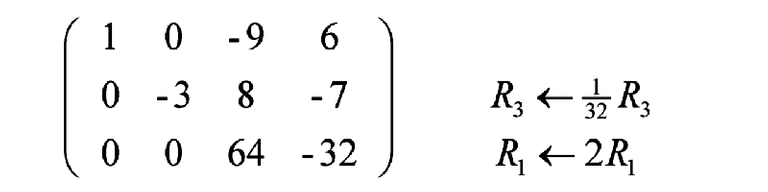
To make our computation easier, we divide row 3 through by the highest common factor in that row, namely 32. Anticipating that 64 will be reduced to 2, the “-9” from row 1 would need a factor of 2 in order to kill it. Accordingly, we multiply row 1 by 2.
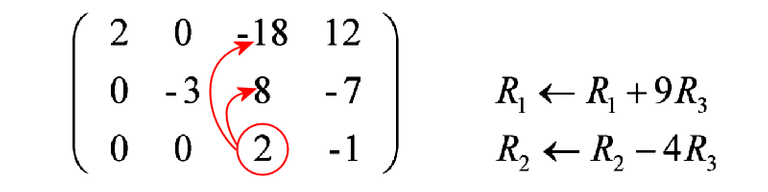Now we use the “2” from row 3 as a pivot element to kill off the other elements in its column. Add 9 times of row 3 to row 1, and subtract 4 times of row 3 from row 2. That would produce the zeros that we want.
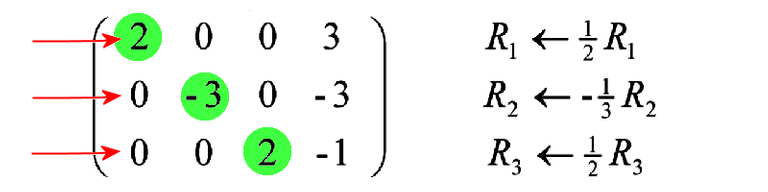We are almost done. We have been using integers and avoiding fractions as much as possible. All we need to do now is to divide each row by its leading non-zero element.
This is the final result, the reduced row-echelon form.
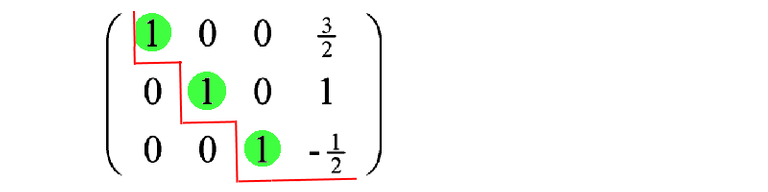
Ta da! I hope you see that this is a very clean way to do the working. If you do it the traditional GJ way (I dare you!), it will very likely be a mess. But if you do it my way, more power to you!
This article is suitable for
- high school students who study Advanced Level Further Mathematics or International Baccalaureate Further Mathematics
- university / college students doing a course in Linear Space (Vector Space) Theory, or Matrix Theory and the like
- anybody who is interested in learning and/or appreciates beautiful and elegant mathematics
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Cheers!!!
@tradersharpe
-- promoting sharp minds
)