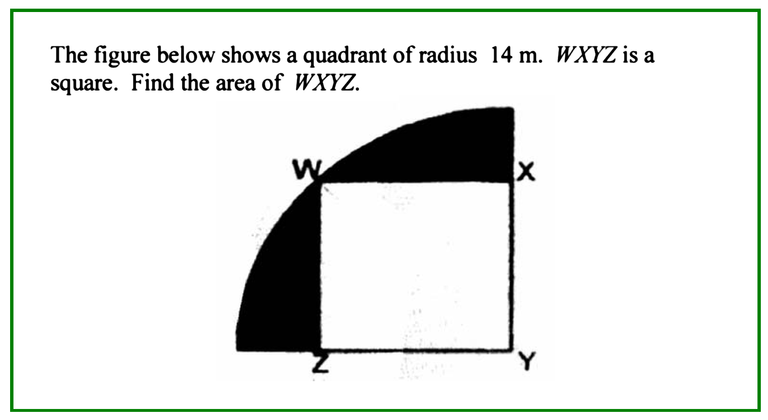
This problem is at around grade 5 to 6 level from Singapore's primary school mathematics curriculum. It is challenging because it seems to require the use of Pythagoras' Theorem. Like: you do not know the length of a side of the square, so you let it be x and the other side is also x. Form the equation, solve it and voilà! You can get the answer!
However, pupils do not learn Pythagoras' Theorem in primary school. It looks like you have to fight the problem with with your hands tied behind your back. Actually, ...
... not quite. There is a trick you can use. In fact examiners have been setting questions like these so much that it has this type of question has become quite common and, maybe, predictable. OK, but what is the trick?
.
.
.
think
.
.
.
think
.
.
.
think
.
.
.
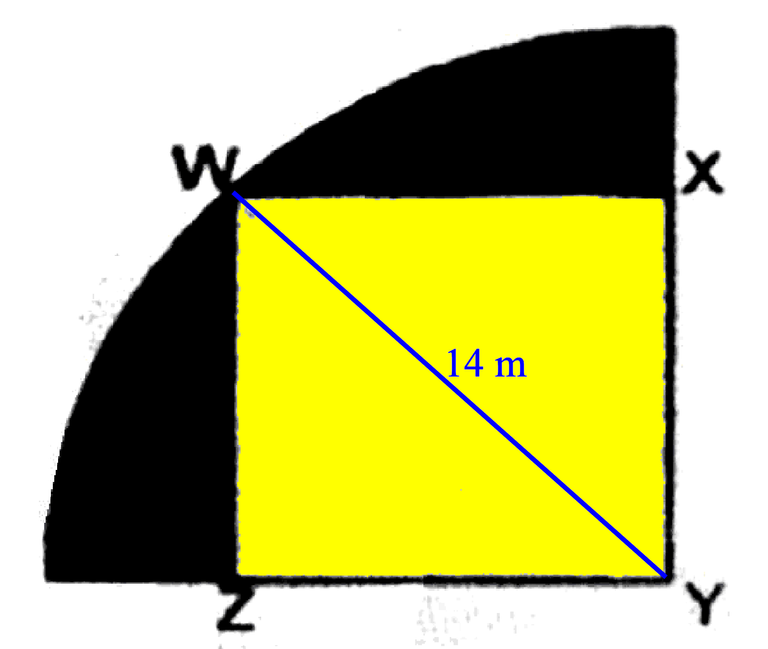
Try to understand the problem. you are given that the radius is 14 m, and that happens to be equal to diagonal of the square (coloured in yellow).
.
.
.
think
.
.
.
think
.
.
.
think
.
.
.
Can you think of an equivalent problem?
.
.
.
think
.
.
.
think
.
.
.
think
.
.
.
Is there something you can do to the area that would leave the area unchanged? (use your imagination)
.
.
.
think
.
.
.
think
.
.
.
think
.
.
.
How about shifting things around?
.
.
.
think
.
.
.
think
.
.
.
think
.
.
.
Got it?
If you did, congratulations!
If you didn't, no worries. It's just a learning experience.
Here is my solution:-
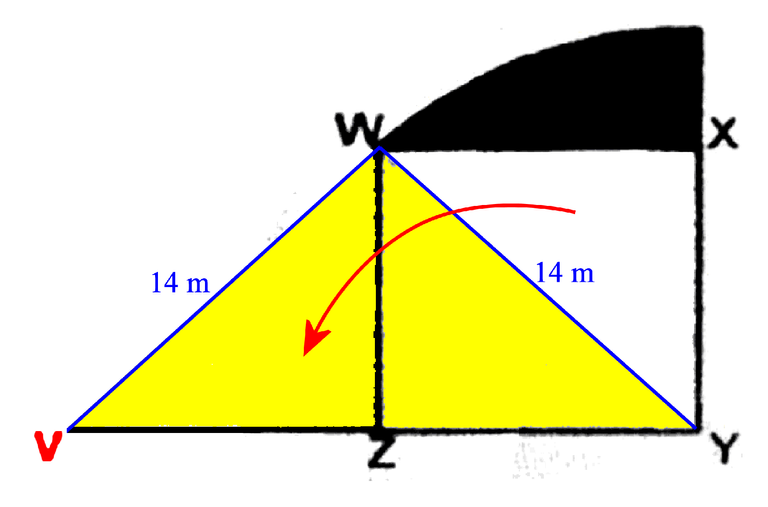
You can move the triangle WYX to a new location, forming triangle WZV. Now notice that you get one big triangle VWY (coloured in yellow) with a right-angled triangle at W, with "base" WY = 14 m and
"height" VW = 14 m. Tilt your head around (or turn your tablet or mobile phone around, with portrait/landscape mode locked) if that helps. The area is the same as before, because we are just moving things around. Now we can easily see that the area is 1/2 × 14 × 14 = 98 m².
Ta da!
Announcements
You might also want to read my recent articles:
Arithmetic Progression in a triangle
If you find my articles useful or interesting, please upvote and resteem them! Thanks !
Cheers!!!
@tradersharpe
-- promoting sharp minds
Excellent
learning post
thats great concept getting of steemit..best of luck..
✌✌✌✌
It is easy to understand mathematics but it is very difficult to understand. Your post is informative. Thanks for sharing.
@alchemage has voted on behalf of @minnowpond. If you would like to recieve upvotes from minnowponds team on all your posts, simply FOLLOW @minnowpond.
To receive an BiggerUpvote send 0.5 SBD to @minnowpond with your posts url as the memo To receive an BiggerUpvote and a reSteem send 1.25SBD to @minnowpond with your posts url as the memo To receive an upvote send 0.25 SBD to @minnowpond with your posts url as the memo To receive an reSteem send 0.75 SBD to @minnowpond with your posts url as the memo To receive an upvote and a reSteem send 1.00SBD to @minnowpond with your posts url as the memoSteemit
I’m not sure if this works but I believe I found a slightly faster way to work out the answer
It states that WXYZ is a square meaning that the two sides that form the triangle WZY must (when squared) equal 14cm (196cm before square rooted).
Well, to find the area of a square, we square the side. In Pythagoras, we square both sides and then square root?
What’s the point in doing all this geometric adjustment when the answer is literally 1/2 of 14 squared? I know this because if 14^2 = 2x^2 (x being the side length a & b in Pythagoras’ theorem, but since we know they’re the same number, they can be represented as a like term, or x). If we simplify this down we get x = root 98. To find it’s area, we multiply root 98 by itself to get 98cm squared, which is the answer